《视觉SLAM十四讲 第二版》笔记及课后习题（第四讲）

读书笔记：李群与李代数

上一讲，我们介绍了三维世界中刚体运动的描述方式，包括旋转矩阵、旋转向量、欧拉角、四元数等若干种方式。我们重点介绍了旋转的表示，但是在SLAM 中，除了表示之外，我们还要对它们进行估计和优化。因为在SLAM 中位姿是未知的，而我们需要解决什么样的相机位姿最符合当前观测数据这样的问题。一种典型的方式是把它构建成一个优化问题，求解最优的R; t，使得误差最小化。
如前所言，旋转矩阵自身是带有约束的（正交且行列式为1）。它们作为优化变量时，会引入额外的约束，使优化变得困难。通过李群——李代数间的转换关系，我们希望把位姿估计变成无约束的优化问题，简化求解方式。
(这一章是纯数学的内容)


李群（Lie Group）：

• 具有连续（光滑）性质的群。
• 既是群也是流形。
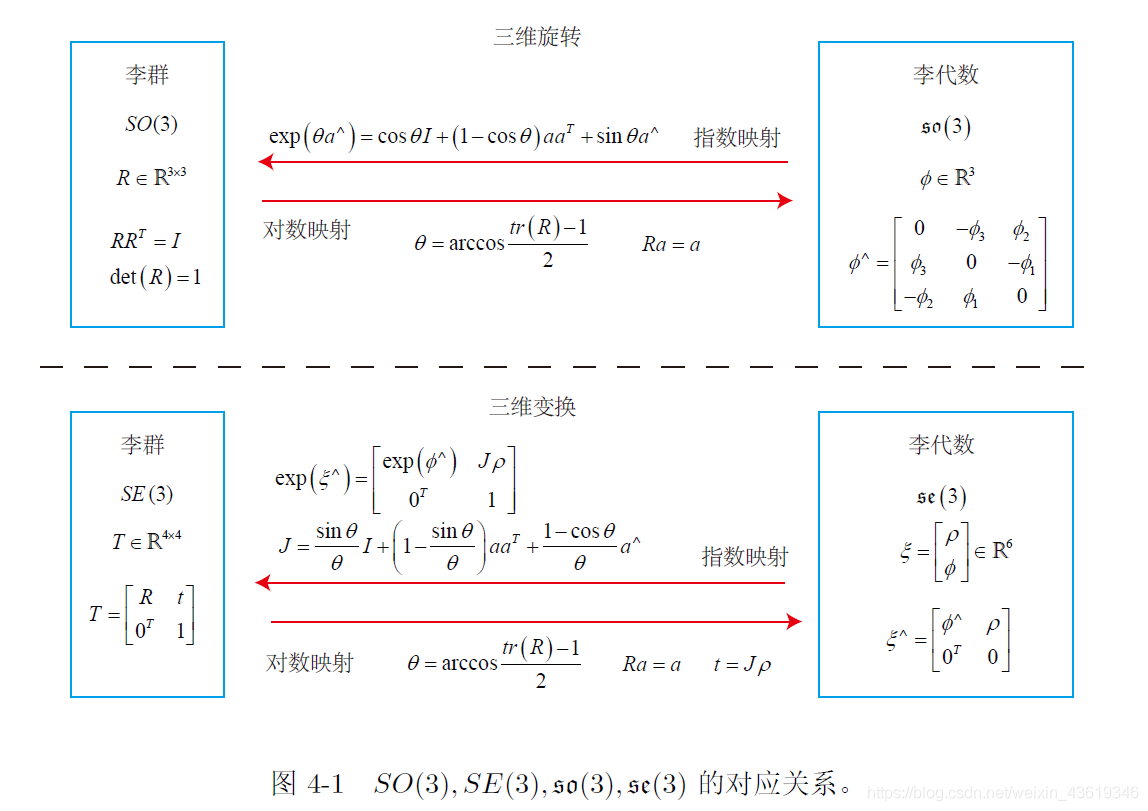
• 直观上看，一个刚体能够连续地在空间中运动，故SO(3)和SE(3)都是李群。但是，SO(3)和SE(3)只有定义良好的乘法，没有加法，所以难以进行取极限、求导等操作。

李代数：与李群对应的一种结构，位于向量空间。

• 通常记作小写的so(3)和se(3)。书中以哥特体突出显示。
• 事实上是李群单位元处的正切空间。

实践部分

useSophus：

依然是出现上一讲的错误：

error: #error This file requires compiler and library support for the ISO C++ 2011 standard. This support must be enabled with the -std=c++11 or -std=gnu++11 compiler options.
 #error This file requires compiler and library support \

在CMakeLists.txt中加入：

set(CMAKE_CXX_FLAGS "-std=c++11 -O2")

然后还得去3rdparty文件夹中安装相应的Sophus库文件，然后编译执行可得结果：

具体结果如下：

/home/wh<