当你迷茫的时候,请回头看看 目录大纲,也许有你意想不到的收获
前言
先准备一些矩阵小知识,后面会大有用处,下面 A,B,C,W 全是矩阵表示
- 右乘提取公共项, A , B , C ∈ R a × b , W ∈ R b × c A,B,C \in R^{a\times b},W\in R^{b\times c} A,B,C∈Ra×b,W∈Rb×c:
[ A ⋅ W B ⋅ W C ⋅ W ] = [ A B C ] W \begin{bmatrix} A\cdot W\\ B\cdot W\\ C\cdot W\\ \end{bmatrix}=\begin{bmatrix} A\\ B\\ C\\ \end{bmatrix}W A⋅WB⋅WC⋅W = ABC W
- 左乘提取公共项, W ∈ R c × b , A , B , C ∈ R a × b W\in R^{c\times b}, A,B,C \in R^{a\times b} W∈Rc×b,A,B,C∈Ra×b:
[ W ⋅ A W ⋅ B W ⋅ C ] = W [ A B C ] \begin{bmatrix} W\cdot A& W\cdot B& W\cdot C& \end{bmatrix} =W\begin{bmatrix} A& B& C& \end{bmatrix} [W⋅AW⋅BW⋅C]=W[ABC]
如果是其他形式,可以先适当变换,变成上面两种形式后再提取公共项,当然,还有些其他形式的,看上去像,但不一定能直接提,例如:
[ W ⋅ A W ⋅ B W ⋅ C ] = [ W 0 0 0 W 0 0 0 W ] [ A B C ] = ( I 3 ⊗ W ) [ A B C ] \begin{bmatrix} W\cdot A\\ W\cdot B\\ W\cdot C\\ \end{bmatrix} =\begin{bmatrix} W & 0 & 0 \\ 0 & W & 0 \\ 0 & 0 & W \end{bmatrix} \begin{bmatrix} A \\ B \\ C \end{bmatrix} =(I_3 \otimes W) \begin{bmatrix} A \\ B \\ C \end{bmatrix} W⋅AW⋅BW⋅C = W000W000W ABC =(I3⊗W) ABC
好了,可以回到主题上来,我们继续往下讲
一元线性回归
上一篇我们讲到了一元线性回归的解法,用的是最小二乘法, 来求解小猪的体重与饭量的规律
y = w x + b y=wx+b y=wx+b
最终一个矩阵运算就搞定了参数,直接上结论:
[ w b ] = [ ∑ i = 1 m x i 2 ∑ i = 1 m x i ∑ i = 1 m x i m ] − 1 [ ∑ i = 1 m x i y i ∑ i = 1 m y i ] \begin{bmatrix} w\\[10pt] b \end{bmatrix} =\begin{bmatrix} \sum\limits_{i=1}^{m}{x_i}^2 & \sum\limits_{i=1}^{m}{x_i} \\[10pt] \sum\limits_{i=1}^{m}{x_i} & m \end{bmatrix}^{-1} \begin{bmatrix} \sum\limits_{i=1}^{m}{x_i y_i}\\[10pt] \sum\limits_{i=1}^{m}y_i \end{bmatrix} wb = i=1∑mxi2i=1∑mxii=1∑mxim −1 i=1∑mxiyii=1∑myi
多元线性回归
假如现在输入不只是一个 x 了,而是多个输入:
y = w 1 x 1 + w 2 x 2 + . . . + b y=w_1x_1+w_2x_2+...+b y=w1x1+w2x2+...+b
还是用小猪的例子来说明,现在小猪是杂食动物,不光吃饭,还会吃糠,吃饲料…
假如小猪现在重 1 斤( b = 1 b=1 b=1),吃一碗饭( x 1 x_1 x1)长 1 斤肉( w 1 = 1 w_1=1 w1=1),吃一碗糠( x 2 x_2 x2)长半斤肉( w 2 = 0.5 w_2=0.5 w2=0.5),吃一碗饲料( x 3 x_3 x3)长 2 斤肉( w 3 = 2 w_3=2 w3=2)…,那么猪的体重就是
y = x 1 + 1 2 x 2 + 2 x 3 + . . . + 1 y=x_1+\frac{1}{2}x_2+2x_3+...+1 y=x1+21x2+2x3+...+1
矩阵形式
一切皆矩阵, 上面的多元函数如果用矩阵的形式可以写成:
y = [ x 1 x 2 . . . 1 ] [ w 1 w 2 . . . b ] y= \begin{bmatrix} x_1&x_2&...&1 \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ ... \\ b \end{bmatrix} y=[x1x2...1] w1w2...b
可以注意到,如果把 b 也当做是一个 w n w_n wn , x x x 矩阵最后的那个 1 也当作是一个输入 x n x_n xn,那么上式可以写成这样一个通用形式:
y = [ x 1 x 2 . . . x n ] [ w 1 w 2 . . . w n ] y= \begin{bmatrix} x_1 & x_2 & ... & x_n \end{bmatrix} \begin{bmatrix} w_1\\ w_2\\ ...\\ w_n\\ \end{bmatrix} y=[x1x2...xn] w1w2...wn
因为观测时会有多个样本数据,假设第 i 个样本的输入为 x i n × 1 x_i^{n\times 1} xin×1, 例如: 1 碗饭,2 碗糠,1 碗饲料 ( x i 1 = 1 , x i 2 = 2 , x i 3 = 1 x_{i1}=1,x_{i2}=2,x_{i3}=1 xi1=1,xi2=2,xi3=1), 样本输出(体重)为标量 y i y_i yi, 预测值为标量 y i ^ \hat{y_i} yi^, 参数为 W n × 1 W^{n\times 1} Wn×1
x i = [ x i 1 x i 2 . . . x i n ] , W = [ w 1 w 2 . . . w n ] y i ^ = x i T W = [ x i 1 x i 2 . . . x i n ] [ w 1 w 2 . . . w n ] x_i=\begin{bmatrix} x_{i1}\\ x_{i2}\\ ...\\ x_{in} \end{bmatrix}, W= \begin{bmatrix} w_1\\ w_2\\ ...\\ w_n \end{bmatrix}\\[10pt] \hat{y_i}=x_i^T W=\begin{bmatrix} x_{i1} & x_{i2} & ... & x_{in} \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ ... \\ w_n \end{bmatrix} xi= xi1xi2...xin ,W= w1w2...wn yi^=xiTW=[xi1xi2...xin] w1w2...wn
假如有 m 个样本, 第 i 个样本的预测值为 y i ^ \hat{y_i} yi^:
y ^ 1 = x 1 T W = [ x 11 x 12 . . . x 1 n ] [ w 1 w 2 . . . w n ] y ^ 2 = x 2 T W = [ x 21 x 22 . . . x 2 n ] [ w 1 w 2 . . . w n ] . . . y ^ m = x m T W = [ x m 1 x m 2 . . . x m n ] [ w 1 w 2 . . . w n ] \hat{y}_1=x_1^T W=\begin{bmatrix} x_{11} & x_{12} & ... & x_{1n} \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ ... \\ w_n \end{bmatrix}\\[10pt] \hat{y}_2=x_2^T W=\begin{bmatrix} x_{21} & x_{22} & ... & x_{2n} \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ ... \\ w_n \end{bmatrix}\\[10pt] ...\\ \hat{y}_m=x_m^T W=\begin{bmatrix} x_{m1} & x_{m2} & ... & x_{mn} \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ ... \\ w_n \end{bmatrix} y^1=x1TW=[x11x12...x1n] w1w2...wn y^2=x2TW=[x21x22...x2n] w1w2...wn ...y^m=xmTW=[xm1xm2...xmn] w1w2...wn
那么可以写成下面的矩阵表示:
Y ^ = [ y ^ 1 y ^ 2 . . . y ^ m ] = [ x 1 T W x 2 T W . . . x m T W ] = [ x 1 T x 2 T . . . x m T ] W = [ x 11 x 12 . . . x 1 n x 21 x 22 . . . x 2 n . . . . . . . . . . . . x m 1 x m 2 . . . x m n ] W \hat{Y}=\begin{bmatrix} \hat{y}_1\\[10pt] \hat{y}_2\\[10pt] ...\\[10pt] \hat{y}_m\\[10pt] \end{bmatrix} =\begin{bmatrix} x_1^T W\\[10pt] x_2^T W\\[10pt] ...\\[10pt] x_m^T W\\[10pt] \end{bmatrix} =\begin{bmatrix} x_1^T\\[10pt] x_2^T \\[10pt] ...\\[10pt] x_m^T \\[10pt] \end{bmatrix} W=\begin{bmatrix} x_{11}&x_{12}&...&x_{1n}\\ x_{21}&x_{22}&...&x_{2n}\\ ...&...&...&...\\ x_{m1}&x_{m2}&...&x_{mn}\\ \end{bmatrix}W Y^= y^1y^2...y^m = x1TWx2TW...xmTW = x1Tx2T...xmT W= x11x21...xm1x12x22...xm2............x1nx2n...xmn W
残差平方和 RSS
令 m 个样本点输入为 X,输出为 Y,样本数据是已知量:
X = [ x 1 T x 2 T . . . x m T ] = [ x 11 x 12 . . . x 1 n x 21 x 22 . . . x 2 n . . . . . . . . . . . . x m 1 x m 2 . . . x m n ] , Y = [ y 1 y 2 . . . y m ] X=\begin{bmatrix} x_1^T\\[10pt] x_2^T \\[10pt] ...\\[10pt] x_m^T \\[10pt] \end{bmatrix} =\begin{bmatrix} x_{11}&x_{12}&...&x_{1n}\\ x_{21}&x_{22}&...&x_{2n}\\ ...&...&...&...\\ x_{m1}&x_{m2}&...&x_{mn}\\ \end{bmatrix}, Y=\begin{bmatrix} y_1\\[10pt] y_2\\[10pt] ...\\[10pt] y_m\\[10pt] \end{bmatrix} X= x1Tx2T...xmT = x11x21...xm1x12x22...xm2............x1nx2n...xmn ,Y= y1y2...ym
则有:
Y ^ = X W , Y ^ ∈ R n × 1 , X ∈ R m × n , W ∈ R n × 1 R S S = ∑ i = 1 m ( y ^ i − y i ) 2 = ∑ i = 1 m ( x i T W − y i ) 2 = [ x 1 T W − y 1 x 2 T W − y 2 . . . x m T W − y m ] T [ x 1 T W − y 1 x 2 T W − y 2 . . . x m T W − y m ] = ( [ x 1 T x 2 T . . . x m T ] W − [ y 1 y 2 . . . y m ] ) T ( [ x 1 T x 2 T . . . x m T ] W − [ y 1 y 2 . . . y m ] ) R S S = ( X W − Y ) T ( X W − Y ) \hat{Y}=XW ,\hat{Y} \in R^{n \times 1}, X\in R^{m \times n}, W \in R^{n \times 1}\\[10pt] RSS=\sum\limits_{i=1}^{m}{(\hat{y}_i-y_i)^2} =\sum\limits_{i=1}^{m}{({x_i}^T W-y_i)^2}\\[10pt] =\begin{bmatrix} {x_1}^TW-y_1 \\[10pt] {x_2}^TW-y_2\\[10pt]...\\[10pt]{x_m}^TW-y_m\\[10pt] \end{bmatrix}^T \begin{bmatrix} {x_1}^TW-y_1 \\[10pt] {x_2}^TW-y_2\\[10pt]...\\[10pt]{x_m}^TW-y_m\\[10pt] \end{bmatrix}\\[10pt]\\ =(\begin{bmatrix} {x_1}^T\\[10pt] {x_2}^T\\[10pt] ...\\[10pt] {x_m}^T\\[10pt] \end{bmatrix}W- \begin{bmatrix} y_1\\[10pt] y_2\\[10pt] ...\\[10pt] y_m\\[10pt] \end{bmatrix} )^T (\begin{bmatrix} {x_1}^T\\[10pt] {x_2}^T\\[10pt] ...\\[10pt] {x_m}^T\\[10pt] \end{bmatrix}W- \begin{bmatrix} y_1\\[10pt] y_2\\[10pt] ...\\[10pt] y_m\\[10pt] \end{bmatrix})\\[10pt] RSS=(XW-Y)^T(XW-Y) Y^=XW,Y^∈Rn×1,X∈Rm×n,W∈Rn×1RSS=i=1∑m(y^i−yi)2=i=1∑m(xiTW−yi)2= x1TW−y1x2TW−y2...xmTW−ym T x1TW−y1x2TW−y2...xmTW−ym =( x1Tx2T...xmT W− y1y2...ym )T( x1Tx2T...xmT W− y1y2...ym )RSS=(XW−Y)T(XW−Y)
最小残差平方和
为了后面求导方便不带一些系数, 引入中间变量 E,令:
E = 1 2 R S S = 1 2 ∑ i = 1 m ( x i T W − y i ) 2 = 1 2 ( X W − Y ) T ( X W − Y ) u i = x i T W − y i = x i 1 w 1 + x i 2 w 2 + . . . + x i n w n − y i E = 1 2 ∑ i = 1 m u i 2 = 1 2 ( u 1 2 + u 2 2 + . . . + u m 2 ) E=\frac{1}{2}RSS=\frac{1}{2}\sum\limits_{i=1}^{m}{({x_i}^T W-y_i)^2}\\[10pt] =\frac{1}{2}(XW-Y)^T(XW-Y)\\[10pt] u_i={x_i}^T W-y_i=x_{i1}w_1+x_{i2}w_2+...+x_{in}w_n-y_i\\[10pt] E=\frac{1}{2}\sum\limits_{i=1}^{m}{u_i}^2=\frac{1}{2}(u_1^2+u_2^2+...+u_m^2) E=21RSS=21i=1∑m(xiTW−yi)2=21(XW−Y)T(XW−Y)ui=xiTW−yi=xi1w1+xi2w2+...+xinwn−yiE=21i=1∑mui2=21(u12+u22+...+um2)
计算准备
∂ E ∂ u i = 1 2 ( u i 2 ) ′ = u i ∂ u i ∂ W = [ ∂ u i ∂ w 1 ∂ u i ∂ w 2 . . . ∂ u i ∂ w n ] ∂ u i ∂ w j = x i j \frac{\partial{E}}{\partial{u_i}}=\frac{1}{2}(u_i^2)'=u_i\\[10pt] \frac{\partial{u_i}}{\partial{W}}= \begin{bmatrix} \frac{\partial{u_i}}{\partial{w_1}}\\[10pt] \frac{\partial{u_i}}{\partial{w_2}}\\[10pt] ...\\[10pt] \frac{\partial{u_i}}{\partial{w_n}}\\[10pt] \end{bmatrix}\\[10pt] \frac{\partial{u_i}}{\partial{w_j}}=x_{ij} ∂ui∂E=21(ui2)′=ui∂W∂ui= ∂w1∂ui∂w2∂ui...∂wn∂ui ∂wj∂ui=xij
w j w_j wj 这个参数会影响到每个样本的输出, 即:
u 1 , u 2 , u 3 , … , u m ⏟ ⇑ w j \underbrace{u_1,u_2,u_3,\dots,u_m}_\Uparrow \\ {w_j} ⇑ u1,u2,u3,…,umwj
那么求 ∂ E ∂ w j \frac{\partial{E}}{\partial{w_j}} ∂wj∂E 就得把所有的影响都加起来,
链式求导
∂ E ∂ w j = ∑ i = 1 m ∂ E ∂ u i ∂ u i ∂ w j = ∑ i = 1 m u i x i j = ∑ i = 1 m ( x i T W − y i ) x i j = [ x 1 T W − y 1 x 2 T W − y 2 . . . x m T W − y m ] T [ x 1 j x 2 j . . . x m j ] = ( X W − Y ) T [ x 1 j x 2 j . . . x m j ] \frac{\partial{E}}{\partial{w_j}}=\sum\limits_{i=1}^{m}\frac{\partial{E}}{\partial{u_i}}\frac{\partial{u_i}}{\partial{w_j}} =\sum\limits_{i=1}^{m}{u_i} {x_{ij}}\\[10pt] =\sum\limits_{i=1}^{m}{({x_i}^TW-y_i)x_{ij}}\\[10pt] =\begin{bmatrix} {x_1}^TW-y_1\\[10pt] {x_2}^TW-y_2\\[10pt] ...\\[10pt] {x_m}^TW-y_m\\[10pt] \end{bmatrix}^T \begin{bmatrix} x_{1j}\\[10pt] x_{2j}\\[10pt] ...\\[10pt] x_{mj}\\[10pt] \end{bmatrix} =(XW-Y)^T\begin{bmatrix} x_{1j}\\[10pt] x_{2j}\\[10pt] ...\\[10pt] x_{mj}\\[10pt] \end{bmatrix}\\ ∂wj∂E=i=1∑m∂ui∂E∂wj∂ui=i=1∑muixij=i=1∑m(xiTW−yi)xij= x1TW−y1x2TW−y2...xmTW−ym T x1jx2j...xmj =(XW−Y)T x1jx2j...xmj
这里有用到前面说到矩阵提取公共项的知识了, 这里是先转置成左乘形式, 再提取公共项
(
X
W
−
Y
)
T
(XW-Y)^T
(XW−Y)T:
∂ E ∂ W = [ ∂ E ∂ w 1 ∂ E ∂ w 2 . . . ∂ E ∂ w n ] = [ ( X W − Y ) T [ x 11 x 21 . . . x m 1 ] ( X W − Y ) T [ x 12 x 22 . . . x m 2 ] . . . ( X W − Y ) T [ x 1 n x 2 n . . . x m n ] ] = ( ( X W − Y ) T X ) T = X T ( X W − Y ) = X T X W − X T Y \frac{\partial{E}}{\partial{W}}=\begin{bmatrix} \frac{\partial{E}}{\partial{w_1}}\\[10pt] \frac{\partial{E}}{\partial{w_2}}\\[10pt] ...\\[10pt] \frac{\partial{E}}{\partial{w_n}}\\[10pt] \end{bmatrix} =\begin{bmatrix} (XW-Y)^T\begin{bmatrix} x_{11}\\[10pt] x_{21}\\[10pt] ...\\[10pt] x_{m1}\\[10pt] \end{bmatrix}\\[10pt] (XW-Y)^T\begin{bmatrix} x_{12}\\[10pt] x_{22}\\[10pt] ...\\[10pt] x_{m2}\\[10pt] \end{bmatrix}\\[10pt] ...\\[10pt] (XW-Y)^T\begin{bmatrix} x_{1n}\\[10pt] x_{2n}\\[10pt] ...\\[10pt] x_{mn}\\[10pt] \end{bmatrix}\\[10pt] \end{bmatrix}\\ % 最终结果 =((XW-Y)^T X)^T\\[10pt] =X^T(XW-Y)\\ =X^TXW-X^TY ∂W∂E= ∂w1∂E∂w2∂E...∂wn∂E = (XW−Y)T x11x21...xm1 (XW−Y)T x12x22...xm2 ...(XW−Y)T x1nx2n...xmn =((XW−Y)TX)T=XT(XW−Y)=XTXW−XTY
矩阵求解参数 W
上面我们求得偏导结果:
∂ E ∂ W = X T X W − X T Y \frac{\partial{E}}{\partial{W}}=X^TXW-X^TY\\[10pt] ∂W∂E=XTXW−XTY
还是令偏导为 0, 最小化残差平方和
∂ E ∂ W = 0 X T X W = X T Y \frac{\partial{E}}{\partial{W}}=0\\[10pt] X^TXW=X^TY ∂W∂E=0XTXW=XTY
要注意,矩阵乘法不可以直接除矩阵, 只能通过矩阵的运算来求解, 当 X T X X^TX XTX 可逆时,
W = ( X T X ) − 1 X T Y W=(X^TX)^{-1}X^TY W=(XTX)−1XTY
这便是多元线性回归的参数求解了
验证
一元函数验证
我们回过头看一元线性回归:
y = w x + b y=wx+b y=wx+b
也可以把它当成两个入参, 另一个入参为 1, 这样就变成了多元线性回归问题了:
x i = [ x i 1 ] , W = [ w b ] X = [ x 1 1 x 2 1 … x m 1 ] x_i=\begin{bmatrix} x_i\\ 1 \end{bmatrix},W=\begin{bmatrix} w\\ b \end{bmatrix}\\[10pt] X=\begin{bmatrix} x_{1} & 1\\ x_{2} & 1\\ \dots \\ x_{m} & 1\\ \end{bmatrix} xi=[xi1],W=[wb]X= x1x2…xm111
那么
Y ^ = [ y 1 ^ y 2 ^ … y m ^ ] = X W = [ x 1 1 x 2 1 … x m 1 ] [ w b ] % Y=XW \hat{Y}=\begin{bmatrix} \hat{y_1}\\ \hat{y_2}\\ \dots \\ \hat{y_m}\\ \end{bmatrix} =XW =\begin{bmatrix} x_{1} & 1\\ x_{2} & 1\\ \dots \\ x_{m} & 1\\ \end{bmatrix}\begin{bmatrix} w\\ b \end{bmatrix} Y^= y1^y2^…ym^ =XW= x1x2…xm111 [wb]
运用我们上面多元线性回归的结论:
W = ( X T X ) − 1 X T Y W=(X^TX)^{-1}X^TY W=(XTX)−1XTY
X T X = [ x 1 x 2 . . . x m 1 1 . . . 1 ] [ x 1 1 x 2 1 … x m 1 ] = [ ∑ i = 1 m x i 2 ∑ i = 1 m x i ∑ i = 1 m x i m ] X T Y = [ x 1 x 2 . . . x m 1 1 . . . 1 ] [ y 1 y 2 … y m ] = [ ∑ i = 1 m x i y i ∑ i = 1 m y i ] X^TX=\begin{bmatrix} x_{1} & x_{2} &...&x_{m} \\ 1 & 1&...&1\\ \end{bmatrix} \begin{bmatrix} x_{1} & 1\\ x_{2} & 1\\ \dots \\ x_{m} & 1\\ \end{bmatrix} =\begin{bmatrix} \sum\limits_{i=1}^{m}{x_{i}^2} & \sum\limits_{i=1}^{m}{x_{i}}\\ \sum\limits_{i=1}^{m}{x_{i}} & m\\ \end{bmatrix}\\[10pt] % Y X^TY=\begin{bmatrix} x_{1} & x_{2} &...&x_{m} \\ 1 & 1&...&1\\ \end{bmatrix}\begin{bmatrix} y_1\\ y_2\\ \dots \\ y_m\\ \end{bmatrix} =\begin{bmatrix} \sum\limits_{i=1}^{m}{x_i y_i}\\[10pt] \sum\limits_{i=1}^{m}y_i \end{bmatrix} XTX=[x11x21......xm1] x1x2…xm111 = i=1∑mxi2i=1∑mxii=1∑mxim XTY=[x11x21......xm1] y1y2…ym = i=1∑mxiyii=1∑myi
所以就得出
W
=
(
X
T
X
)
−
1
X
T
Y
=
[
∑
i
=
1
m
x
i
2
∑
i
=
1
m
x
i
∑
i
=
1
m
x
i
m
]
−
1
[
∑
i
=
1
m
x
i
y
i
∑
i
=
1
m
y
i
]
W=(X^TX)^{-1}X^TY= \begin{bmatrix} \sum\limits_{i=1}^{m}{x_{i}^2} & \sum\limits_{i=1}^{m}{x_{i}}\\ \sum\limits_{i=1}^{m}{x_{i}} & m\\ \end{bmatrix}^{-1} \begin{bmatrix} \sum\limits_{i=1}^{m}{x_i y_i}\\[10pt] \sum\limits_{i=1}^{m}y_i \end{bmatrix}
W=(XTX)−1XTY=
i=1∑mxi2i=1∑mxii=1∑mxim
−1
i=1∑mxiyii=1∑myi
结果与开头一元线性回归的解相呼应了, 确实是一样的
[ w b ] = [ ∑ i = 1 m x i 2 ∑ i = 1 m x i ∑ i = 1 m x i m ] − 1 [ ∑ i = 1 m x i y i ∑ i = 1 m y i ] \begin{bmatrix} w\\[10pt] b \end{bmatrix} =\begin{bmatrix} \sum\limits_{i=1}^{m}{x_i}^2 & \sum\limits_{i=1}^{m}{x_i} \\[10pt] \sum\limits_{i=1}^{m}{x_i} & m \end{bmatrix}^{-1} \begin{bmatrix} \sum\limits_{i=1}^{m}{x_i y_i}\\[10pt] \sum\limits_{i=1}^{m}y_i \end{bmatrix} wb = i=1∑mxi2i=1∑mxii=1∑mxim −1 i=1∑mxiyii=1∑myi
python 程序验证
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体 - macOS
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'Heiti TC', 'STHeiti']
plt.rcParams['axes.unicode_minus'] = False
# 1. 生成模拟数据
np.random.seed(42) # 设置随机种子保证可重复性
# 真实参数
true_w1 = 2.5
true_w2 = -1.8
true_bias = 3.0
# 生成样本数据
n_samples = 100
x1 = np.random.uniform(-5, 5, n_samples)
x2 = np.random.uniform(-5, 5, n_samples)
# 添加噪声的真实y值
noise = np.random.normal(0, 2, n_samples)
y = true_w1 * x1 + true_w2 * x2 + true_bias + noise
print(f"真实参数: w1={true_w1:.2f}, w2={true_w2:.2f}, bias={true_bias:.2f}")
# 2. 计算RSS函数
def compute_rss(w1, w2, bias, x1, x2, y):
"""计算残差平方和"""
y_pred = w1 * x1 + w2 * x2 + bias
rss = np.sum((y - y_pred) ** 2)
return rss
# 3. 创建参数网格
w1_range = np.linspace(0, 5, 50) # w1参数范围
w2_range = np.linspace(-4, 1, 50) # w2参数范围
W1, W2 = np.meshgrid(w1_range, w2_range)
# 固定偏置项为真实值(或者可以也作为变量)
fixed_bias = true_bias
# 计算每个参数组合的RSS
RSS = np.zeros_like(W1)
for i in range(W1.shape[0]):
for j in range(W1.shape[1]):
RSS[i, j] = compute_rss(W1[i, j], W2[i, j], fixed_bias, x1, x2, y)
# 4. 绘制RSS曲面图
fig = plt.figure(figsize=(16, 6))
# 子图1:3D曲面图
ax1 = fig.add_subplot(121, projection='3d')
surf = ax1.plot_surface(W1, W2, RSS, cmap='viridis', alpha=0.8,
linewidth=0, antialiased=True)
# 标记最小值点
min_idx = np.unravel_index(np.argmin(RSS), RSS.shape)
min_w1 = W1[min_idx]
min_w2 = W2[min_idx]
min_rss = RSS[min_idx]
ax1.scatter([min_w1], [min_w2], [min_rss], color='red', s=100,
label=f'最小RSS点\nw1={min_w1:.2f}\nw2={min_w2:.2f}')
ax1.set_xlabel('参数 w1', labelpad=10)
ax1.set_ylabel('参数 w2', labelpad=10)
ax1.set_zlabel('RSS (残差平方和)', labelpad=10)
ax1.set_title('RSS 与参数关系曲面图\n(3D视图)', pad=20)
ax1.legend()
# 子图2:等高线图
ax2 = fig.add_subplot(122)
contour = ax2.contour(W1, W2, RSS, levels=20, cmap='viridis')
ax2.clabel(contour, inline=True, fontsize=8)
# 标记真实参数点
ax2.scatter(true_w1, true_w2, color='blue', s=100, marker='*',
label=f'真实参数\nw1={true_w1:.2f}\nw2={true_w2:.2f}')
# 标记估计参数点
ax2.scatter(min_w1, min_w2, color='red', s=100, marker='o',
label=f'估计参数\nw1={min_w1:.2f}\nw2={min_w2:.2f}')
ax2.set_xlabel('参数 w1')
ax2.set_ylabel('参数 w2')
ax2.set_title('RSS 等高线图', pad=20)
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 5. 使用正规方程验证结果
print("\n=== 正规方程验证 ===")
# 添加偏置项
X_matrix = np.column_stack([np.ones(n_samples), x1, x2])
# 正规方程: w = (X^T X)^(-1) X^T y
w_optimal = np.linalg.inv(X_matrix.T @ X_matrix) @ X_matrix.T @ y
print(f"正规方程解: bias={w_optimal[0]:.4f}, w1={w_optimal[1]:.4f}, w2={w_optimal[2]:.4f}")
print(f"真实参数: bias={true_bias:.4f}, w1={true_w1:.4f}, w2={true_w2:.4f}")
# 6. 绘制数据点和回归平面
fig2 = plt.figure(figsize=(12, 5))
# 子图1:数据点散点图
ax3 = fig2.add_subplot(121, projection='3d')
# 绘制数据点
scatter = ax3.scatter(x1, x2, y, c=y, cmap='viridis', s=30, alpha=0.7)
# 创建回归平面
x1_plane = np.linspace(-5, 5, 20)
x2_plane = np.linspace(-5, 5, 20)
X1_plane, X2_plane = np.meshgrid(x1_plane, x2_plane)
Y_plane = w_optimal[1] * X1_plane + w_optimal[2] * X2_plane + w_optimal[0]
# 绘制回归平面
ax3.plot_surface(X1_plane, X2_plane, Y_plane, alpha=0.3, color='red')
ax3.set_xlabel('特征 x1')
ax3.set_ylabel('特征 x2')
ax3.set_zlabel('目标值 y')
ax3.set_title('数据点与回归平面', pad=20)
# 子图2:预测值与真实值对比
ax4 = fig2.add_subplot(122)
y_pred = X_matrix @ w_optimal
ax4.scatter(y, y_pred, alpha=0.7)
ax4.plot([y.min(), y.max()], [y.min(), y.max()], 'r--', lw=2)
ax4.set_xlabel('真实值')
ax4.set_ylabel('预测值')
ax4.set_title('预测值与真实值对比', pad=20)
ax4.grid(True, alpha=0.3)
# 计算R²
r_squared = 1 - np.sum((y - y_pred) ** 2) / np.sum((y - np.mean(y)) ** 2)
ax4.text(0.05, 0.95, f'R² = {r_squared:.4f}', transform=ax4.transAxes,
fontsize=12, verticalalignment='top', bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))
plt.tight_layout()
plt.show()
结果展示
真实参数: w1=2.50, w2=-1.80, bias=3.00
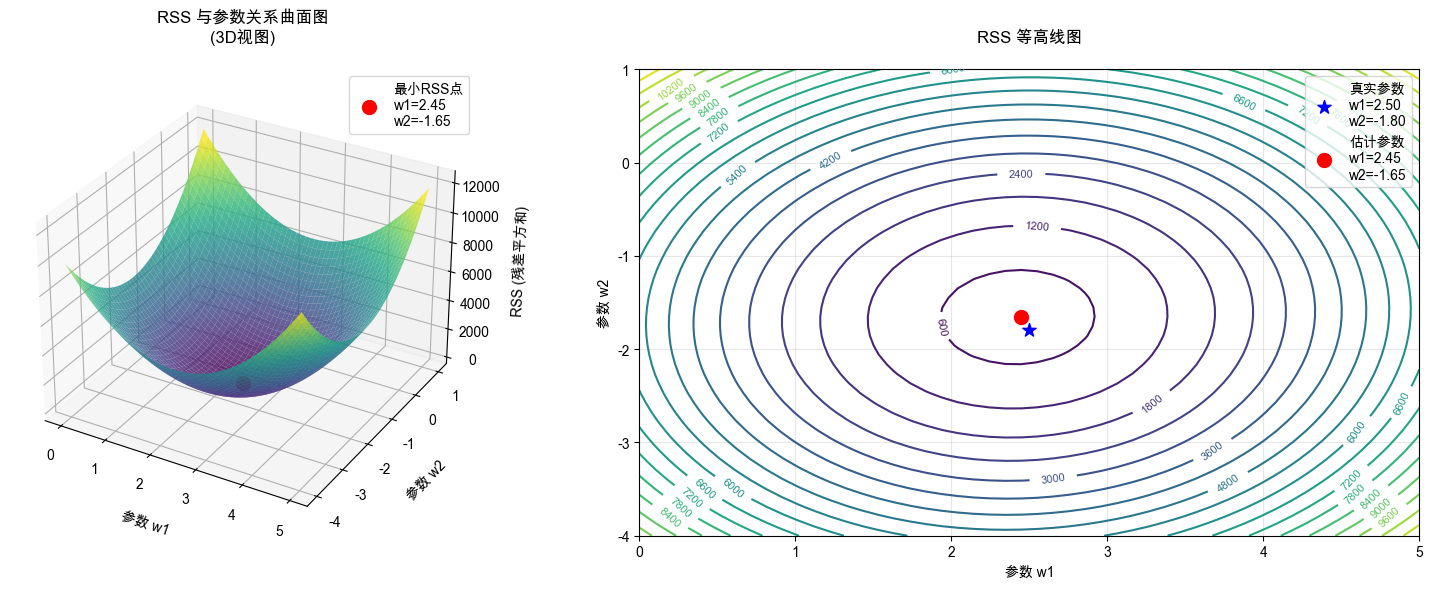
=== 正规方程验证 ===
正规方程解: bias=3.1988, w1=2.4317, w2=-1.6561
真实参数: bias=3.0000, w1=2.5000, w2=-1.8000
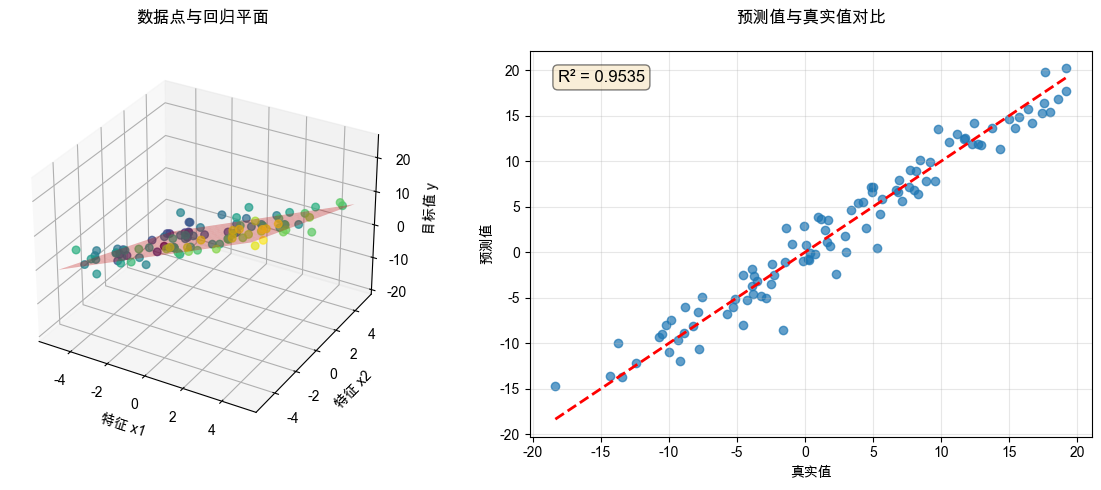






















 1460
1460

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










