一、为什么要用典型相关分析
典型相关分析研究的是两组变量之间的关系,如{x1, x2, x3}和{y1, y2, y3}两组变量之间的关系。
具体来说,变量间的相关关系可以分为以下几种:
- 两个变量间的线性相关关系,可用简单相关系数
- 一个变量与多个变量之间的线性相关关系,可用复相关系数。
- 多个变量与多个变量间的相关关系,使用典型相关关系
二、典型相关分析的基本原理
典型相关分析在研究两组变量间的线性相关关系时,将每一组变量作为一个整体进行分析。它采用类似于主成分分析(PCA)的方法,在每一组变量中都选择若干个有代表性的综合指标,这些综合指标是原始变量的线性组合,代表了原始变量的大部分信息,且两组综合指标的相关程度最大。
简单地说,对于{x1, x2, x3}和{y1, y2, y3}两组变量,我们先求出能体现x和y最大相关性的一对变量u1,v1:u1是{x1, x2, x3}的线性组合,v1是{y1, y2, y3}的线性组合。
然后再类似的求第二、第三对典型相关变量,然后我们就得到两组典型相关变量{u1,u2,u3}和{v1,v2,v3}。三对典型相关变量是彼此不相关的,它们反应了变量组x和y之间的相关关系。
当两组变量的数量不一致时,那么可提取到的典型变量个数就等于较少数据组的变量个数,如对于{x1, x2, x3}和{y1, y2},可提取的典型变量为2个。
三、实例分析
1.数据
某个研究人员收集了600名大学新生的三个心理变量,四个学术变量(标准化考试成绩) 。他希望研究者3个心理变量与4个学术变量间的相关关系。
也就是说,我们要分析
- 变量组x{外向倾向,自我概念,动机水平}
- 变量组y{阅读成绩,写作成绩,数学成绩,理科成绩}
之间的相关关系。数据如下图所示:
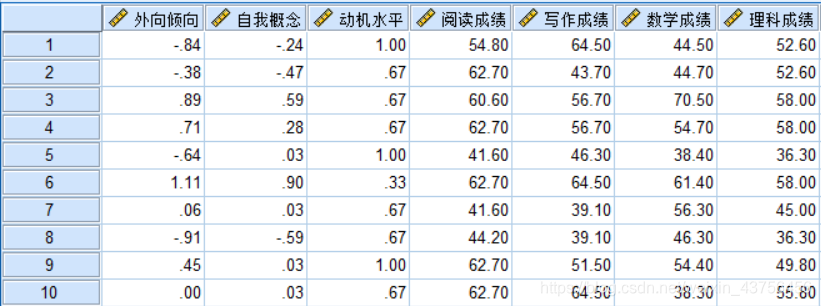
2.分析
在SPSS25中,选择:分析→相关→典型相关性,在选项中勾选成对相关性
(备注:SPSS23前的版本没有这个选项,需要使用自定义宏)


3.结果
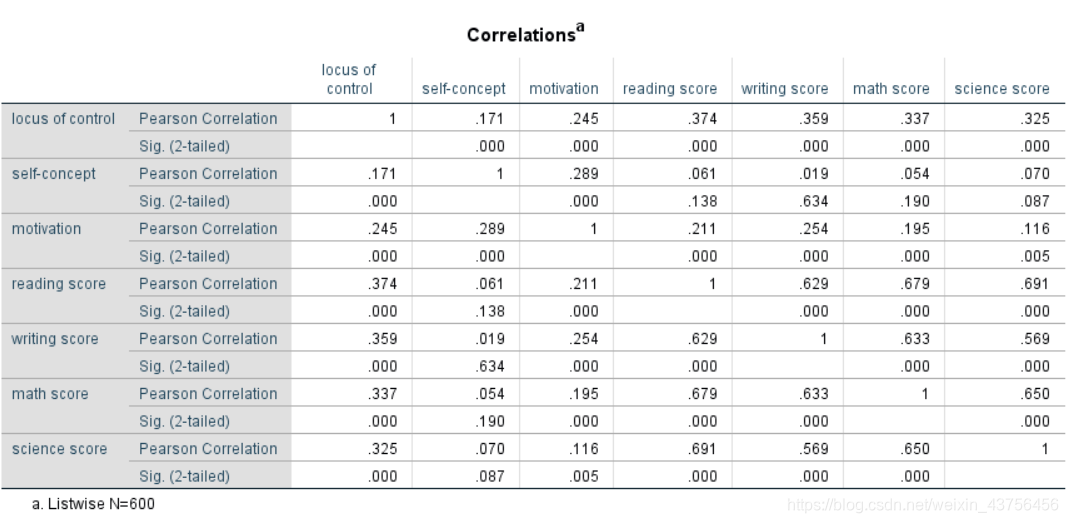
此图反映了各变量间的相关系数,从中可以看出不同变量间的相关程度。
如果组内变量间的相关系数高,说明两者包含的信息有重叠部分;如果组间变量相关系数高,则说明两者有一定相关性(- -!)。

此图给出了典型相关系数及其检验,结果表明前两个典型相关系数是显著的,因此我们选择前两个典型相关变量进行解释。
具体来说,第一对典型相关变量的相关系数是0.446,p< .001;第二对典型相关变量的相关系数是0.153,p= .025
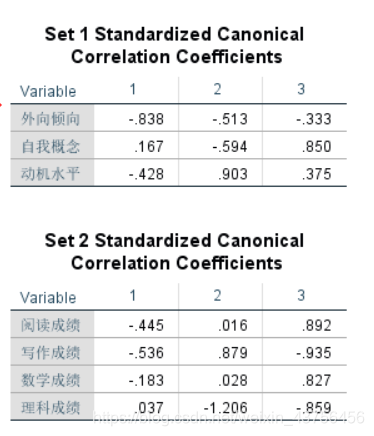

上图分别是两组变量的标准化相关系数和未标准化的相关系数。
根据此图,可以写出各典型变量的表达式,如对于第一对典型变量u1和v1:
其标准化的表达式为(Z外向倾向表示将该变量标准化后的值):
u1 = -0.838*Z外向倾向+0.167*Z自我概念-0.428*Z动机水平
v1 = -0.445*Z阅读成绩-0.536*Z写作成绩-0.183*Z数学成绩+0.037*Z理科成绩
非标准化的表达式为
u1 = -1.250*外向倾向+0.237*自我概念-1.249*动机水平
v1 = -0.044*阅读成绩-0.055*写作成绩-0.019*数学成绩+0.004*理科成绩
PS:再讲解一下两者的一些不同之处:
标准化的系数由于经过标准化,因此系数相互之间是可比的,用处是用于比较不同自变量对应变量的影响程度。比如在set1的标准化系数中,外向倾向的系数是-0.838,自我概念的系数是0.167,因此我们可以认为外向倾向对成绩的影响比自我概念影响更大。
而未标准化的系数因为每个变量没有标准化,量纲不一样,因此不能直接用系数大小比较自变量贡献程度,它的用处是可以用于计算CCA得分,(直接用系数乘以原始数据)

上图是冗余分析的结果,它说明各典型变量对各变量组方差解释的比例。
以上是个人对典型相关分析学习的总结笔记,如有错误,欢迎讨论和指正。
























 8729
8729

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








