《信号与系统》第二章 常用信号及LTI系统的时域分析

2.1 常用信号及其基本特性

在数字信号处理与系统分析领域中，有着大量复杂的信号，而这些信号基本都是由一些常用信号组成的，常用的信号主要有以下几种：

1. 连续及离散时间复指数信号
2. 连续及离散时间阶跃信号
3. 连续时间冲激信号
4. 离散时间单位样值信号
   
   

2.1.1 复指数信号

一、连续时间复指数信号

形如

$$x\left(t\right)=e^{st}（-\infty <t<\infty ,s=\sigma +j\omega ）$$

的信号，称为连续时间复指数信号，根据参数的取值不同，还可以将复指数信号分为下列几个种类：

信号种类	参数取值	时间函数
直流信号	σ=0, ω=0	$$x(t)=1$$
实指数信号	σ≠0, ω=0	$$x(t)=e^{\sigma t}$$
虚指数信号	σ=0, ω≠0	$$x(t)=cos(\omega t)+jsin(\omega t)$$
复指数信号	σ≠0, ω≠0	$$x(t)=e^{\sigma t}cos(\omega t)+j{e}^{\sigma t}sin(\omega t)$$

根据上表可知，σ和ω的取值（s的取值）直接决定了复指数信号的种类，在数学上，将σOω坐标面称为s平面，因此有序数对(σ,ω)在s平面中所处的位置决定了复指数信号的类型，具体情况如下：

位置(σ,ω) (σ>0,ω>0)	信号种类
原点(0,0)	直流信号
σ轴正半轴(σ,0)	指数信号(单调递增）
第二象限(-σ,ω)	衰减振荡信号
σ轴负半轴(-σ,0)	指数信号(单调递增）

二、离散时间复指数信号

而在时间离散的情况下，形如

$$x\left[n\right]=z^n={\left(r{e}^{j\Omega }\right)}^n=r^n{e}^{j\Omega n}（z=r{e}^{j\Omega },-\infty <n<+\infty ）$$

的信号，称为离散时间复指数信号或复指数序列，其中r为复数z的模，Ω为幅角

复指数序列中的z与连续复指数信号中的s性质较为类似，s常采用直角坐标系s=σ+jω的方法表示，而z则常使用极坐标的方式进行表示，二者均属于复常数，因此根据r和Ω的取值，复指数序列同样也可以分为多个种类：

信号种类	参数取值	时间函数
实指数序列（单调递增）	Ω=0	$$x[n]=r^n$$
实指数序列（单调递减）	Ω=π	$$x[n]=(-r{)}^n$$
虚指数序列	r=1	$$x[n]=e^{j\Omega n}=cos[\Omega n]+jsin[\Omega n]$$
复指数序列		$$x[n]=r^{n}cos[\Omega n]+j{r}^{n}sin[\Omega n]$$

以复数z的实部Re[z]为横轴，虚部j·Im[z]作为纵轴，建立z平面，可知：
|z|<1（单位圆内），对应指数衰减振荡序列；
|z|=1（单位圆上），对应正弦序列；
|z|>1（单位圆外），对应指数增长振荡序列。

2虚指数序列的实部是正弦序列，其数学表达式为：$x\left[n\right]=\cos \left[{\Omega }_0\cdot n+\phi \right]$，时间连续正弦信号可转化为正弦序列：$x\left(t\right)=\cos \left({\omega }_0\cdot t+\phi \right)\stackrel{t=nT}{⟶}x[n]=cos[{\omega }_{0}nT+\phi ]$，此处Ω₀与ω₀分别为离散时间和连续时间的基本角频率，此处的T为离散时间的采样间隔，通常采样间隔恒定不变。由此可得Ω₀与ω₀的关系为：

$${\Omega }_0={\omega }_{0}T=\frac{{\omega }_0}{f_s}=2\pi \frac{f_0}{f_s}$$

其中
${\omega }_0——模拟角频率（rad/s）$
${\Omega }_0——数字域频率（rad）$
$T——采样频率（s）$
$f_0——模拟频率（Hz）$
$f_s——采样频率（Hz）$

因此，数字域频率Ω是模拟角频率ω对采样频率的归一化。

2.1.2 单位阶跃信号

一、连续时间单位阶跃信号

定义一个连续时间信号，该信号在t=0之前信号的数值均为0，在t=0之后均为1，则称该信号为连续时间单位阶跃信号，其定义的符号表达式如下：

$$u\left(t\right)=\{\begin{array}{l}1，t>0\\ 0，t<0\end{array}$$

将该定义推广，得：

$$Au\left(t-t_0\right)=\{\begin{array}{l}A，t>t_0\\ 0，t<t_0\end{array}$$

在实际应用中，单位阶跃信号常用于表示电源开关的接入状态，也常用于表示其他信号，比如：

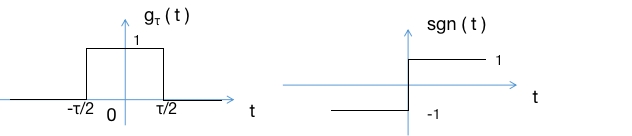
矩形脉冲：指阶跃时间远小于顶部持续时间的平顶脉冲，常用单位阶跃信号进行表示：

$$g_{\tau }\left(t\right)=u\left(t+\frac{\tau }{2}\right)-u\left(t-\frac{\tau }{2}\right)$$

符号函数：当t>0时数值为1，t<0时数值为-1的函数称为符号函数，对任意函数f(t)，都有f(t)=sgn(t)·|f(t)|，其符号表达式表示为：

$$sgn\left(t\right)=\{\begin{array}{l}1,t>0\\ -1,t<0\end{array}=u(t)-u(-t)=2\cdot u(t)-1$$

二、离散时间单位阶跃信号

与连续时间单位阶跃信号类似，离散时间单位阶跃信号（或称单位阶跃序列）在n=0之前信号的数值均为0，在n=0之后均为1，但是有所不同的是，连续时间单位阶跃信号在t=0上没有定义，而单位阶跃序列在n=0时取常数1，符号表达式为：

$$u\left[n\right]=\{\begin{array}{l}1，n\ge 0\\ 0，n<0\end{array}$$

类似的，将单位阶跃序列推广，可得：

$$Au\left[n-k\right]=\{\begin{array}{l}A，n\ge k\\ 0，n<k\end{array}$$

2.1.3 连续时间单位冲激信号

当矩阵脉冲从-τ/2到τ/2的积分为1，宽度τ无限趋近于0，高度1/τ趋近于无穷大时，该信号的作用时间极短，相应物理量极大。数学上称这一类信号为连续时间单位冲激信号，其数学定义为：

$$\delta \left(t\right)=\{\begin{array}{l}\delta \left(t\right)=0，t\ne 0\\ \\ {\int }_{-\infty }^{\infty }\delta \left(t\right)dt=1\end{array}$$

推广为：

$$A\delta \left(t\right)=\{\begin{array}{l}A\delta \left(t\right)=0，t\ne 0\\ \\ {\int }_{-\infty }^{\infty }A\delta \left(t\right)dt=A\end{array}$$

连续时间单位冲激信号主要有以下性质：

1. 筛选性：设x(t)为在t₀处连续的普通函数，则有：

   $$x(t)\delta \left(t-t_0\right)=x(t_0)\delta \left(t-t_0\right)$$

   该式表明，通过信号x(t)与冲激函数δ(t-t₀)相乘，可筛选出连续时间信号x(t)在t₀处的函数值x(t₀)，其相乘结果仍为冲激信号，在t₀瞬间数值仍趋于无穷大，但冲激强度由 1 变为x(t₀)。

2. 取样性：设x(t)为在t₀处连续的普通函数，则有：

   $${\int }_{-\infty }^{\infty }x(t)\delta \left(t-t_0\right)dt=x(t_0)$$

   该式表明，通过信号x(t)与冲激函数δ(t-t₀)相乘，并在时间域 (-∞,+∞) 上积分，可得到x(t)在t₀处的取值x(t₀)。一个普通函数x(t)与冲激函数δ(t)乘积下的面积等于x(t)在冲激瞬间的值。

3. 展缩性：$\delta \left(at+b\right)=\frac{1}{\left|a\right|}\delta \left(t+\frac{b}{a}\right)$

   证明如下：

   ${\int }_{-\infty }^{\infty }\delta \left(at+b\right)f\left(t\right)dt\stackrel{\tau =at+b}{=}\frac{1}{\left|a\right|}{\int }_{-\infty }^{\infty }\delta \left(\tau \right)f\left(\frac{\tau -b}{a}\right)d\tau =\frac{1}{\left|a\right|}f\left(-\frac{b}{a}\right)$
   
   $={\int }_{-\infty }^{\infty }\frac{1}{\left|a\right|}\delta \left(t+\frac{b}{a}\right)f\left(t\right)dt=\frac{1}{\left|a\right|}f\left(-\frac{b}{a}\right)$
   
   $\therefore \delta \left(at+b\right)=\frac{1}{\left|a\right|}\delta \left(t+\frac{b}{a}\right)$

   根据这一性质，令a=-1、b=0，可得δ(-t)=δ(t)，因此冲激信号δ(t)是偶函数。

连续时间单位冲激信号可由连续时间单位阶跃信号经微分得到：

$$\delta \left(t\right)=\frac{d}{dt}u\left(t\right)$$

也就是说通过对单位冲激信号积分为可得到单位阶跃信号：

$${\int }_{-\infty }^t\delta \left(\tau \right)d\tau =u\left(t\right)$$

单位冲激信号的微分称为冲激偶信号，由微分的性质可以得出冲击偶信号属于奇函数，对冲击偶信号进一步求微分可得高阶冲激信号。

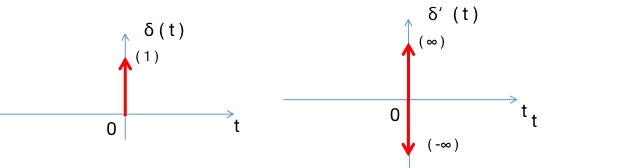
2.1.4 离散时间单位样值信号

定义一个离散时间信号，该信号仅在n=0时数值为1，在n≠0时数值均为0，则称该信号为离散时间单位样值信号，又称为单位样值序列，其定义的符号表达式如下：

$$\delta \left[n\right]=\{\begin{array}{l}1，n=0\\ 0，n\ne 0\end{array}$$

将该定义推广，得：

$$\delta \left[n-k\right]=\{\begin{array}{l}1，n=k\\ 0，n\ne k\end{array}$$

对于任意一个离散时间信号，都可以使用δ[n]及δ[n-k]的线性加权和表示

$$x\left[n\right]=\sum _{k=-\infty }^{\infty }x\left[k\right]\delta \left[n-k\right]$$

例如下图

可表示为：x[n]=x[-2]·δ[n+2] + x[-1]·δ[n+1] + x[0]·δ[n] + x[1]·δ[n-1] + x[2]·δ[n-2]

对比单位阶跃序列，很容易发现单位样值序列可由单位阶跃序列的差分得到，其符号表达式为

$$\delta [n]=u[n]-u[n-1]$$

2.2 信号的时域运算

2.2.1 信号的微积分运算

信号的微分：$\frac{d}{dt}x\left(t\right)=x^{\prime }\left(t\right)$

信号的积分：$x^{\left(-1\right)}\left(t\right)={\int }_{-\infty }^{t}x\left(\tau \right)d\tau$

2.2.2 信号的展缩、翻转、平移

一、连续时间信号的展缩、翻转、平移

1. 平移： x(t) → x(t+b) b > 0 时，左移；b < 0 时，右移。
2. 翻转： x(t) → x(-t) 波形以纵轴为轴左右翻转。
3. 展缩：（尺度变换） x(t)→x(at)

$a>0时，t\in \left[t_1,t_2\right]\to t\in \left[\frac{t_1}{a},\frac{t_2}{a}\right]$

$若a>1，波形被压缩为原来的\frac{1}{a}$

$若a<1，波形被扩展为原来的a倍$

4. 展缩、翻转、平移： 可将按照任意顺序进行上述计算，例如：

二、离散时间信号的展缩、翻转、平移

离散时间信号的展缩、翻转、平移： x[n]→x[an+b]，a、b为实常数，a≠0

离散时间信号波形的翻转和平移的方法与连续信号相同，而展缩变换有所不同，由于离散时间信号时间不连续的特性，导致该类信号在进行压缩时会导致部分信号的丢失；在进行扩展的时候会导致信号在部分时间上没有定义。

2.2.2 信号的分解

信号可以分解成以下几种形式：

1. 信号分解为奇偶信号之和
2. 信号分解为基本信号的有限项之和
3. 信号的因子分解
4. 信号分解为矩阵脉冲之和
5. 信号分解为正交信号分量之和

这里着重介绍信号分解为矩形脉冲之和的方法

由上图，将连续时间信号x(t)分解为多个矩形脉冲之和，这些矩形脉冲的宽度均为τ，则

$$x(t)\approx x(0)\cdot g(t)+x(\Delta \tau )\cdot g(t-\Delta \tau )+...+x(n\Delta \tau )\cdot g(t-n\Delta \tau )$$

$={\sum }_{k=-\infty }^{\infty }x(n\Delta \tau )\cdot g(t-n\Delta \tau )={\sum }_{k=-\infty }^{\infty }x(n\Delta \tau )\cdot \frac{g(t-n\Delta \tau )}{\Delta \tau }\cdot \Delta \tau$

当Δτ → 0时，n Δ τ → τ ，$\frac{g(t-n\Delta \tau )}{\Delta \tau }$ → δ (t-τ )，Δ τ → d τ

$x(t)={\int }_{-\infty }^{\infty }x(\tau )\cdot \delta \left(t-\tau \right)d\tau$

类似地，任意离散时间信号可分解为：
$$x[n]=\sum _{k=-\infty }^{\infty }x[k]\cdot \delta [n-k]$$

2.3 卷积积分、卷积和

2.3.1 卷积的定义

卷积积分：$x_1(t)\ast x_2(t)={\int }_{-\infty }^{\infty }{x}_1\left(\tau \right)x_2(t-\tau )d\tau$

卷积和：$x_1[n]\ast x_2[n]={\sum }_{k=-\infty }^{\infty }{x}_1[k]\cdot x_2[n-k]$

卷积的物理意义：揭示了LTI系统的零状态响应与输入信号、系统单位冲激响应之间的关系。

2.3.2 卷积的图解法

卷积积分运算：$x_1(t)\ast x_2(t)={\int }_{-\infty }^{\infty }{x}_1\left(\tau \right)x_2(t-\tau )d\tau$实际上包含了四个步骤：

1. 换元 t→τ
2. 翻转 x₂(τ)→x₂(-τ)
3. 移位 x₂(-τ)→x₂(t-τ)
4. 相乘积分

$p_1(t)$与$p_2(t)$的卷积运算 $p_1(t)\ast p_2(t)$ 具体图解如下：

可以看出，两个有限长信号卷积，卷积后信号的长度为原两信号长度之和，起始时刻为原信号起始时刻之和。

卷积和运算：$x_1[n]\ast x_2[n]={\sum }_{k=-\infty }^{\infty }{x}_1[k]\cdot x_2[n-k]$同样包含了四个步骤：

1. 换元 n→k
2. 翻转 x₂[k]→x₂[-k]
3. 移位 x₂[-k]→x₂[n-k]
4. 相乘求和

$x_1[n]$与$x_2[n]$的卷积运算 $x_1[n]\ast x_2[n]$ 具体图解如下：

可以看出，两个有限长序列卷积，卷积后序列的长度为原两序列长度和-1，起始时刻为原序列起始时间之和。

对于卷积和，还可以使用下图所示的竖式法

遵循的规则：

1. 右端对齐
2. 各点分别相乘相加，不进位
3. 起始序号为两序列起始序号之和

2.3.3 卷积的性质

1. 卷积代数

1. 交换律：$x_1(t)\ast x_2(t)=x_2(t)\ast x_1(t)$
2. 分配律：$x_1(t)\ast [x_2(t)+x_3(t)]=x_1(t)\ast x_2(t)+x_1(t)\ast x_3(t)$
3. 结合律：$[x_1(t)\ast x_2(t)]\ast x_3(t)=x_1(t)\ast [x_2(t)\ast x_3(t)]$
   
   

2. 冲激信号的卷积特性

1. $\delta (t)\ast x(t)=x(t)$，称δ(t)是卷积积分的单位元。
   证明：$\delta (t)\ast x(t)={\int }_{-\infty }^{\infty }\delta (\tau )x(t-\tau )d\tau =x(t)$

2. $\delta (t-t_0)\ast x(t)=x(t-t_0)$，称$\delta (t-t_0)$为延时器。
   推论：如果$x_1(t)\ast x_2(t)=y(t)$，那么$x_1(t)\ast x_2(t-t_0)=y(t-t_0)$
   $x_1(t-t_1)\ast x_2(t-t_2)=y(t-t_1-t_2)$
   该性质称为卷积的时不变性，该性质对于离散样值信号同样有效：
   $\delta [n]\ast x[n]=x[n]\delta [n-n_0]\ast x[n]=x[n-n_0]$
   
   

3.卷积的微分特性

${\delta }^{\prime }(t)\ast x(t)=x^{\prime }(t)$，称δ’(t)是微分器。
推论：${\delta }^{(n)}(t)\ast x(t)=x^{(n)}(t)$

$\frac{d{x}_1(t)}{dt}\ast x_2(t)=x_1(t)\ast \frac{d{x}_2(t)}{dt}=\frac{d}{dt}[x_1(t)\ast x_2(t)]$

4.卷积的积分特性

$x(t)\ast u(t)={\int }_{-\infty }^{t}x(\tau )d\tau$，称u(t)是模拟积分器。

证明：$x(t)\ast u(t)={\int }_{-\infty }^{\infty }x(\tau )u(t-\tau )d\tau ={\int }_{-\infty }^{t}x(\tau )d\tau$

推论：$\left[{\int }_{-\infty }^t{x}_1\left(\tau \right)d\tau \right]\ast x_2\left(t\right)$

$=x_1\left(t\right)\ast \left[{\int }_{-\infty }^t{x}_2\left(\tau \right)d\tau \right]$

$={\int }_{-\infty }^t\left[x_1\left(\tau \right)\ast x_2\left(\tau \right)d\tau \right]$

$x_1(t)\ast x_2(t)={\int }_{-\infty }^t{x}_1(\tau )d\tau \ast \frac{d{x}_2(t)}{dt}=\frac{d{x}_1(t)}{dt}\ast {\int }_{-\infty }^t{x}_2(\tau )d\tau$

上式成立条件：$$\underset{t\to -\infty }{\lim }{x}_1\left(t\right)=\underset{t\to -\infty }{\lim }{x}_2\left(t\right)=0$$

5.卷积的求和特性

$x[n]\ast u[n]={\sum }_{k=-\infty }^{n}x[k]$，称u[n]是数字积分器。

推论：$\left[{\sum }_{k=-\infty }^n{x}_1\left[k\right]\right]\ast x_2\left[n\right]=x_1\left[n\right]\ast \left[{\sum }_{k=-\infty }^n{x}_2\left[k\right]\right]={\sum }_{k=-\infty }^n\left[x_1\left[k\right]\ast x_2\left[k\right]\right]$

2.4 连续时间系统的时域分析

2.4.1 连续时间系统的数学模型——微分方程

1. 微分方程的基本形式：

$$\frac{d^n}{d{t}^n}y\left(t\right)+a_{n-1}\frac{d^{n-1}}{d{t}^{n-1}}y\left(t\right)+\dots +a_1\frac{d}{dt}y\left(t\right)+a_{0}y\left(t\right)=b_m\frac{d^m}{d{t}^m}x\left(t\right)+\dots +b_1\frac{d}{dt}x\left(t\right)+b_{0}x\left(t\right)$$

2. 微分方程的求解方法

1. 时域解法
    微分方程的解分为齐次解y_n(t)和特解y_f(t)。y(t)=y_n(t)+y_f(t)

2. 零输入/零状态解法
    全响应=零输入响应y_zi(t)+零状态响应y_zs(t)。y(t)=y_zi(t)+y_zs(t)

3. 变换域解法
    通过拉普拉斯变换求解微分方程。

   此处重点讨论零输入/零响应解法

     全响应=零输入响应y_zi(t)+零状态响应y_zs(t)。y(t)=y_zi(t)+y_zs(t)
     零输入响应：输入x(t)为零，仅由初始状态产生的响应，记为y_zi(t)
     零状态响应：初始状态为零，仅由输入信号x(t)产生的响应，记为y_zs(t)

   通常取t=0时刻作为起始时刻
   输入信号在t=0时刻之后作用于系统，记为x(t)=f(t)·u(t)
   $t=0^{-}$时刻系统的状态称为$t=0^{-}$状态，记为$y(0^{-})$、$y^{\prime }(0^{-})$…
   $t=0^{+}$时刻系统的状态称为$t=0^{+}$状态，记为$y(0^{+})$、$y^{\prime }(0^{+})$…

   零输入响应由于其输入为0，根据微分方程齐次方程求解：

   $$\frac{d^n}{d{t}^n}y\left(t\right)+a_{n-1}\frac{d^{n-1}}{d{t}^{n-1}}y\left(t\right)+\dots +a_1\frac{d}{dt}y\left(t\right)+a_{0}y\left(t\right)=0$$

   其特征方程为：$D(\lambda )={\lambda }^n+a_{n-1}{\lambda }^{n-1}+...+a_1\lambda +a_0=0$
   通过因式分解，解得特征根 ${\lambda }_1,{\lambda }_2,...,{\lambda }_n$

   特征根为单实根时，可得微分方程的齐次通解：$y_{zi}(t)=c_1{e}^{{\lambda }_{1}t}+c_2{e}^{{\lambda }_{2}t}+...+c_n{e}^{{\lambda }_{n}t}$

   其中，$e^{\lambda t}$称为特征模式，这也是连续时间指数信号一般表示成$e^{st}$的形式的原因。
   零输入响应时齐次方程的解，其形式与时域解法中的齐次通解相同。
   待定系数由初始状态$y_{zi}(0^{-})=y(0^{-})、y_{zi}^{\prime }(0^{-})=y^{\prime }(0^{-})$确定。

   $例1：RLC电路如图所示，i(t)为输出，R=3\Omega ，L=1H，C=\frac{1}{2}F，$

   $输入x(t)=10e^{-3t}u(t)，i(0^{-})=0，u_c(0^{-})=5V，试求其零输入响应i_{zi}(t)$

   

   根据电感、电阻、电容与电流的关系，建立将该电路的模型为：

   $$L{i}^{\prime \prime }(t)+R{i}^{\prime }(t)+\frac{1}{C}i(t)=x^{\prime }(t)$$

   代入参数得：

   $$i^{\prime \prime }(t)+3i^{\prime }(t)+2i(t)=x^{\prime }(t)$$

   由此可得微分方程的特征方程为：

   $${\lambda }^2+3\lambda +2=0$$

   因式分解得：

   $$(\lambda +1)(\lambda +2)=0$$

   由此可得特征根为：

   $${\lambda }_1=-1，{\lambda }_2=-2$$

   将特征根代入可得通解为：

   $$i_{zi}(t)=C_1{e}^{-t}+C_2{e}^{-2t}，t>0$$

   该式中仍有$C_1、C_2$两个未知量，通过待定系数法解出：

   由基尔霍夫电压定律（KVL）得：

   $$L{i}^{\prime }(0^{-})+Ri(0^{-})+u_c(0^{-})=0$$

   解得：

   $$i^{\prime }(0^{-})=-5$$

   对$i_{zi}(t)=C_1{e}^{-t}+C_2{e}^{-2}$求导，得：

   $$i^{\prime }(t)=-C_1{e}^{-t}-2C_2{e}^{-2t}$$

   将$i(0^{-})=0，u_c(0^{-})=5V$代入通解，得：

   $$\{\begin{array}{l}i\left(0\right)=C_1+C_2=0\\ i^{\prime }\left(0\right)=-C_1-2C_2=-5\end{array}$$

   解得：

   $$\{\begin{array}{l}{C}_1=-5\\ C_2=5\end{array}$$

   从而该RLC电路系统的零输入响应为：

   $$i_{zi}(t)=-5e^{-t}+5e^{-2t}，t>0$$

3. 单位冲激响应

系统初始状态为零，输入为单位冲激信号$\delta (t)$时的响应，称为单位冲激响应，记为h(t)，将h(t)代入微分方程

$$\frac{d^n}{d{t}^n}y\left(t\right)+a_{n-1}\frac{d^{n-1}}{d{t}^{n-1}}y\left(t\right)+\dots +a_1\frac{d}{dt}y\left(t\right)+a_{0}y\left(t\right)=b_m\frac{d^m}{d{t}^m}x\left(t\right)+\dots +b_1\frac{d}{dt}x\left(t\right)+b_{0}x\left(t\right)$$

可得适用于单位冲激响应的微分方程：

$$h^{(n)}(t)+a_{n-1}{h}^{(n-1)}(t)+...+a_{0}h(t)=b_m{\delta }^{(m)}(t)+...+b_1{\delta }^{\prime }(t)+b_0\delta (t)$$

由于该方程右侧由高阶冲激信号构成，只在t=0处不为零，在其他位置均为零，因此可以通过求齐次通解的方法来求解h(t)中t≠0的部分，其通解表示为特征模式项之和：

$$y(t)=c_1{e}^{{\lambda }_{1}t}+c_2{e}^{{\lambda }_{2}t}+...+c_n{e}^{{\lambda }_{n}t}$$

将通解与单位阶跃信号相乘，表示t>0时的情况

当t=0时，需要考虑高阶冲激信号产生的响应，该响应取决于单位冲激响应微分方程中的最高阶数m和n的大小：

1. 当n>m时，$h(t)=$[特征模式项之和]$u(t)$
2. 当n=m时，$h(t)=b_m+$[特征模式项之和]$u(t)$
3. 当n<m时，$h(t)$会产生高阶冲激信号

$例2：已知某LTI系统y^{\prime \prime }(t)+3y^{\prime }(t)+2y(t)=x^{\prime }(t)，试求其单位冲激响应h(t)$

根据

$$y^{\prime \prime }(t)+3y^{\prime }(t)+2y(t)=x^{\prime }(t)$$

代入$\delta (t)$可得：

$$h^{\prime \prime }(t)+3h^{\prime }(t)+2h(t)={\delta }^{\prime }(t)$$

可得特征方程：

$${\lambda }^2+3\lambda +2=0$$

解得特征根：

$${\lambda }_1=-1，{\lambda }_2=-2$$

由此可得单位冲激响应：

$$h(t)=(C_1{e}^{-t}+C_2{e}^{-2t})u(t)$$

$$\begin{array}{rl}{h}^{\prime }(t)& =(C_1{e}^{-t}+C_2{e}^{-2t})\delta (t)+(-C_1{e}^{-t}-2C_2{e}^{-2t})u(t)\\ & =(C_1+C_2)\delta (t)+(-C_1{e}^{-t}-2C_2{e}^{-2t})u(t)\end{array}$$

$$h^{\prime \prime }(t)=(C_1+C_2){\delta }^{\prime }(t)+(-C_1-2C_2)\delta (t)+(C_1{e}^{-t}+4C_2{e}^{-2t})u(t)$$

通过冲激平衡法，将$h^{\prime \prime }(t)、h^{\prime }(t)、h(t)$代入$h^{\prime \prime }(t)+3h^{\prime }(t)+2h(t)={\delta }^{\prime }(t)$，解得：

$$C_1=-1，C_2=2$$

由此可得单位冲激响应：

$$h(t)=(-e^{-t}+2e^{-2t})u(t)$$

4. 零状态响应

因为系统单位冲激响应为

$$\delta (t)\to h(t)$$

根据时不变性：

$$\delta (t-n\Delta \tau )\to h(t-n\Delta \tau )$$

根据齐次性：

$$x(n\Delta \tau )\delta (t-n\Delta \tau )\Delta \tau \to x(n\Delta \tau )h(t-n\Delta \tau )\Delta \tau$$

根据可加性：

$$\sum _{n=-\infty }^{\infty }x(n\Delta \tau )\delta (t-n\Delta \tau )\Delta \tau \to \sum _{n=-\infty }^{\infty }x(n\Delta \tau )h(t-n\Delta \tau )\Delta \tau$$

当$\Delta \tau \to 0$时，可以得出：

$$x(t)={\int }_{-\infty }^{\infty }x(\tau )\delta (t-\tau )d\tau \to y_{zs}(t)={\int }_{-\infty }^{\infty }x(\tau )h(t-\tau )d\tau$$

首先分析$x(t)$和$\delta (t)$的关系：

$$\begin{array}{rl}x(t)& ={\int }_{-\infty }^{\infty }x(\tau )\delta (t-\tau )d\tau \\ & =x(t)\ast \delta (t)\end{array}$$

称为“信号的分解特性”。以$\delta (t)$为基本信号，将任意的信号$x(t)$分解为$\delta (t)$的线性加权组合。

而$y_{zs}(t)$和$h(t)$的关系：

$$y_{zs}(t)={\int }_{-\infty }^{\infty }x(\tau )h(t-\tau )d\tau$$

称为“响应的分解特性”，以$h(t)$为基本响应，将$x(t)$产生的$y_{zs}(t)$分解为$h(t)$的线性加权组合，因此：

$$零状态响应=输入信号\ast 单位冲激响应$$

5.响应模式分析

$例2：RLC电路如图所示，i(t)为输出，R=3\Omega ，L=1H，C=\frac{1}{2}F，$

$输入x(t)=10e^{-3t}u(t)，i(0^{-})=0，u_c(0^{-})=5V，试求其全输入响应i(t)$

由例1：

$$i^{\prime \prime }(t)+3i^{\prime }(t)+2i(t)=x^{\prime }(t)$$

$${\lambda }^2+3\lambda +2=0$$

$${\lambda }_1=-1，{\lambda }_2=-2$$

零输入响应：

$$i_{zi}(t)=-5e^{-t}+5e^{-2t}$$

单位冲激响应：

$$h(t)=(-e^{-t}+2e^{-2t})u(t)$$

零状态响应：

$$\begin{array}{rl}{i}_{zs}(t)& =x(t)\ast h(t)\\ & =(-5e^{-t}+20e^{-2t}-15e^{-3t})u(t)\end{array}$$

将零状态响应与零输入响应相加，得全响应：

$$\begin{array}{rl}i(t)& =i_{zi}(t)+i_{zs}(t)\\ & =(-5e^{-t}+5e^{-2t})u(t)+(-5e^{-t}+20e^{-2t}-15e^{-3t})u(t)\end{array}$$

整理可得：

$$i(t)=(-10e^{-t}+25e^{-2t}-15e^{-3t})u(t)$$

其中，$-10e^{-t}+25e^{-2t}$被称为自然响应，也称为自由响应或固有响应，自然响应是由系统特征模式决定的那部分响应，记作$y_n(t)$；
而$-15e^{-3t}$则被称为强迫响应,强迫响应是由激励信号决定的响应，记作$y_f(t)$。

整理上述全响应、零输入响应、零状态响应、自然响应和强迫响应的关系可得：

$$\begin{array}{rl}全响应& =零输入响应+零状态响应\\ 全响应& =自然响应+强迫响应\\ & \\ 自然响应& =零输入响应+零状态响应中由系统特征根决定的部分\\ 强迫响应& =零状态响应中由输入信号特征模式决定的部分\\ & \\ 零输入响应& \ne 自然响应=一部分自然响应=微分方程的齐次解\\ 零状态响应& \ne 强迫响应=另一部分自然响应+强迫响应=微分方程的特解\end{array}$$

另外，全响应还可以分解为瞬态响应与稳态响应，瞬态响应指的是系统响应中随着时间的增加而衰减，并且最终完全消失的分量；而那些对着时间的增加一直保留的分量称为稳态响应。

6. 系统的稳定性和因果性分析

1. 如果系统对任何一个有界输入，输出也有界，则称该系统为有界输出稳定系统（BIBO稳定系统），简称稳定系统。
   即$|x(t)|<A$，则$|y(t)|<B$