学习笔记 位置编码 Position Embedding

Position Encodings in Hung-yi Lee

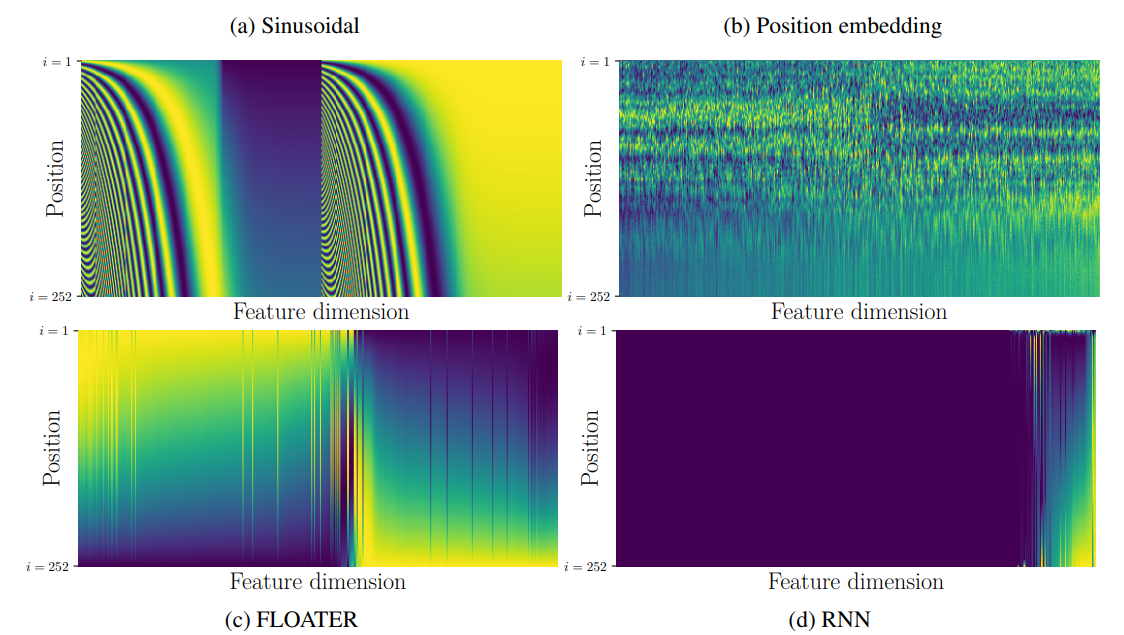
1. Attention is All you Need

$${\mathbf{p}}_i^{(1)}[j]=\{\begin{array}{ll}\sin \left(i\cdot c^{\frac{j}{d}}\right)& \text{ if }j\text{ is even }\\ \cos \left(i\cdot c^{\frac{j-1}{d}}\right)& \text{ if }j\text{ is odd }\end{array}$$

2. Universal transformers

$P^t\in {\mathbb{R}}^{m\times d}$ above are fixed, constant, two-dimensional (position, time) coordinate embeddings, obtained by computing the sinusoidal position embedding vectors as defined in (Vaswani et al., 2017) for the positions $1\le i\le m$ and the time-step $1\le t\le T$ separately for each vector-dimension $1\le j\le d$, and summing:

$$\begin{array}{rl}{P}_{i,2j}^t& =\sin \left(i/10000^{2j/d}\right)+\sin \left(t/10000^{2j/d}\right)\\ P_{i,2j+1}^t& =\cos \left(i/10000^{2j/d}\right)+\cos \left(t/10000^{2j/d}\right).\end{array}$$

or
$${\mathbf{p}}_i^{(n)}[j]=\{\begin{array}{ll}\sin \left(i\cdot c^{\frac{j}{d}}\right)+\sin \left(n\cdot c^{\frac{j}{d}}\right)& \text{ if }j\text{ is even }\\ \cos \left(i\cdot c^{\frac{j-1}{d}}\right)+\cos \left(n\cdot c^{\frac{j-1}{d}}\right)& \text{ if }j\text{ is odd }\end{array}$$

3. Learnable Position Encodings

4. Learning to encode position for transformer with continuous dynamical model

$${\mathbf{p}}^{(n)}(t)={\mathbf{p}}^{(n)}(s)+{\int }_s^t{\mathbf{h}}^{(n)}\left(\tau ,{\mathbf{p}}^{(n)}(\tau );{\mathbf{\theta }}_h^{(n)}\right)\mathrm{d}\tau$$

Position Encodings in Papers with Code

1. Absolute Position Encodings

Absolute Position Encodings are a type of position embeddings for [Transformer-based models] where positional encodings are added to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimension $d_{\text{model }}$ as the embeddings, so that the two can be summed. In the original implementation, sine and cosine functions of different frequencies are used:
$$\begin{array}{c}\mathrm{P}\mathrm{E}(\text{ pos },2i)=\sin \left(pos/10000^{2i/d_{modd}}\right)\\ \mathrm{P}\mathrm{E}(pos,2i+1)=\cos \left(pos/10000^{2i/d_{modd}}\right)\end{array}$$
where pos is the position and $i$ is the dimension. That is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from $2\pi$ to $10000\cdot 2\pi$. This function was chosen because the authors hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k,{\mathrm{P}\mathrm{E}}_{\text{pos }+k}$ can be represented as a linear function of ${\mathrm{P}\mathrm{E}}_{\text{pos }}$.

来源： Papers With Code, D2L.ai

2. Relative Position Encodings

Relative Position Encodings are a type of position embeddings for Transformer-based models that attempts to exploit pairwise, relative positional information. Relative positional information is supplied to the model on two levels: values and keys. This becomes apparent in the two modified self-attention equations shown below. First, relative positional information is supplied to the model as an additional component to the keys
$$e_{ij}=\frac{x_i{W}^Q{\left(x_j{W}^K+a_{ij}^K\right)}^T}{\sqrt{d_z}}$$
Here $a$ is an edge representation for the inputs $x_i$ and $x_j$. The softmax operation remains unchanged from vanilla self-attention. Then relative positional information is supplied again as a sub-component of the values matrix:
$$z_i=\sum _{j=1}^n{\alpha }_{ij}\left(x_j{W}^V+a_{ij}^V\right)$$
In other words, instead of simply combining semantic embeddings with absolute positional ones, relative positional information is added to keys and values on the fly during attention calculation.

来源： Papers With Code, Jake Tae

3. Rotary Position Embedding

Rotary Position Embedding, or RoPE, is a type of position embedding which encodes absolute positional information with rotation matrix and naturally incorporates explicit relative position dependency in self-attention formulation. Notably, RoPE comes with valuable properties such as flexibility of being expand to any sequence lengths, decaying inter-token dependency with increasing relative distances, and capability of equipping the linear self-attention with relative position encoding.

来源： Papers With Code, RoFormer

4. Conditional Positional Encoding

Conditional Positional Encoding, or CPE, is a type of positional encoding for vision transformers. Unlike previous fixed or learnable positional encodings, which are predefined and independent of input tokens, CPE is dynamically generated and conditioned on the local neighborhood of the input tokens. As a result, CPE aims to generalize to the input sequences that are longer than what the model has ever seen during training. CPE can also keep the desired translation-invariance in the image classification task. CPE can be implemented with a Position Encoding Generator (PEG) and incorporated into the current Transformer framework.

来源： Papers With Code, Xiangxiang Chu

5. Attention with Linear Biases

ALiBi, or Attention with Linear Biases, is an alternative to position embeddings for inference extrapolation in Transformer models. When computing the attention scores for each head, the ALiBi method adds a constant bias to each attention score $\left({\mathbf{q}}_i\cdot {\mathbf{k}}_j,\text{left}\right)$ As in the unmodified attention sublayer, the softmax function is then applied to these scores, and the rest of the computation is left unmodified. m is a head-specific scalar that is set and not learned throughout training. When using ALiBi no positional embeddings are added at the bottom of the network.

来源： Papers With Code, Ofir Press

参考资料：

[1] Self-Attention and Positional Encoding

[2] How Positional Embeddings work in Self-Attention (code in Pytorch) | AI Summer (theaisummer.com)

[3] An Overview of Position Embeddings | Papers With Code