用VAE生成图像

变分自编码器是自编码器的改进版本，自编码器AE是一种无监督学习，但它无法产生新的内容，变分自编码器对其潜在空间进行拓展，使其满足正态分布，情况就大不一样了。

自编码器AE，auto-encoder

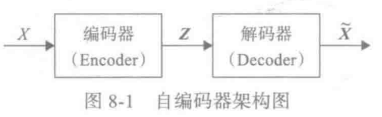
自编码器是通过对输入X进行编码后得到一个低维的向量z，然后根据这个向量还原出输入X。通过对比X与$\stackrel{\sim }{X}$的误差，再利用神经网络去训练使得误差逐渐减小，从而达到非监督学习的目的。
下图为AE的架构图:

AE和VAE的区别：

自编码器不能随意产生合理的潜在变量，从而导致它无法产生新的内容。因为潜在变量Z都是编码器从原始图片中产生的。为了解决这一问题，研究人员对潜在空间Z(潜在变量对应的空间) 增加一些约束，使 Z 满足正态分布，由此就出现了VAE模型， VAE对编码器添加约束，就是强迫它产生服从单位正态分布的潜在变量。正是这种约束，把VAE和 AE 区分开来。

AE的用处是什么呢？

Auto-Encoder有什么用处呢？它好像是将input经过encoder压缩，然后再经过decoder进行reconstruction，然后再经过MSE进行计算loss，是这样的过程吧？那它其实没有生成功能唉，那这个AE有什么用处呢？

Auto-Encoder（自编码器）确实是你描述的那样，它包括一个编码器（encoder）将输入数据压缩成一个较小的潜在空间表示，然后一个解码器（decoder）将其重构回原始数据形式。尽管自编码器的直接输出是对输入的重构，但它在诸多场景下都有重要的应用，具体包括但不限于以下几个方面：

1. 数据降维：自编码器将高维数据压缩成低维表示，这对可视化、数据存储以及处理高维数据非常有帮助。与PCA（Principal Component Analysis）等传统方法相比，自编码器能够捕捉到更复杂的非线性关系。

2. 特征学习：自编码器可以自动学习数据中的重要特征。这些特征可以在后续的机器学习任务（如分类、聚类等）中用作输入，往往能提高模型的性能。

3. 去噪（Denoising）：去噪自编码器（Denoising Auto-Encoder，DAE）是一个自编码器的一种变体，它可以从含有噪声的输入中恢复出无噪声的原始数据，因此在图像处理、信号处理等领域有广泛应用。

4. 生成模型：虽说基础的自编码器没有生成功能，但其变体，比如变分自编码器（Variational Auto-Encoder，VAE），能够生成新的数据样本。VAE学到的潜在空间分布可以用于生成相似的但未见过的样本，这在图像生成、语音合成等领域有重要应用。

5. 异常检测：自编码器可以用来检测异常值（Outlier）。训练好的自编码器可以非常好地重构正常数据，但对异常数据的重构效果比较差。通过计算重构误差，可以识别出异常数据点。这在入侵检测、质量控制等领域非常有用。

6. 超分辨率：自编码器也可以用于提高图像分辨率（super-resolution）。它可以将低分辨率的图像输入到网络中，通过解码器生成高分辨率的图像。

通过以上几种应用，你可以看到，自编码器虽然直接输出的是输入数据的重构，但它的编码能力、特征提取能力以及变种的生成能力使其在许多机器学习和数据处理任务中都能发挥重要作用。

请你具体讲一下，它为什么可以用于去噪呢？它如何用于异常检测和超分辨率呢

当然可以，下面我将详细解释一下自编码器在去噪、异常检测和超分辨率这些方面的应用机制。

去噪（Denoising）
去噪自编码器（Denoising Auto-Encoder, DAE）的基本思想是将受噪声污染的输入数据恢复到没有噪声的原始数据形式。具体流程如下：

1. 数据扰动：在构建去噪自编码器的数据集时，首先需要对原始数据进行扰动，加入噪声，生成包含噪声的数据集。

2. 模型训练：用这些包含噪声的输入数据训练自编码器，目标是让模型学习到将这些带噪声的数据还原到原始的无噪声数据。损失函数通常是计算重构数据和原始无噪声数据之间的误差，如均方误差（MSE）。

3. 去噪过程：训练好的去噪自编码器能够接收包含噪声的输入，并输出尽可能接近原始无噪声数据的重构结果。因此，模型学会了如何消除噪声。

异常检测（Anomaly Detection）
自编码器可以在异常检测中发挥作用的原因在于：

1. 训练阶段：自编码器使用大量的正常数据进行训练，它学会了如何有效地重构这些正常数据。

2. 检测阶段：当输入数据为正常数据时，由于自编码器已经学习到了其结构，重构误差会很低。而当输入数据为异常数据时，由于这些数据在训练过程中没有见到过，模型无法有效地重构它们，导致重构误差较高。

3. 判别过程：通过设定一个阈值，如果某个输入数据的重构误差超过这个阈值，就可以认为它是异常数据。这种方法特别适合应用于工业质控、网络入侵检测等领域。

超分辨率（Super-Resolution）
超分辨率任务是指从低分辨率图像生成高分辨率图像。自编码器可以通过以下方式解决这个问题：

1. 数据预处理：首先将高分辨率图像缩放为低分辨率图像，生成训练数据对。

2. 网络架构：构建自编码器的架构，其中编码器部分将低分辨率图像的特征提取出来，解码器部分将这些特征重新映射到高分辨率图像空间。

3. 模型训练：使用低分辨率图像作为输入，高分辨率图像作为目标，训练自编码器模型，损失函数依然是重构误差。

4. 超分辨率生成：训练好的模型能够接受低分辨率图像作为输入，并通过解码器生成高分辨率图像。因此，模型学会了如何从低分辨率图像中恢复细节和生成高分辨率图像。

综述
通过利用自编码器的编码-解码结构，我们能够让模型学习复杂的映射关系。此结构在去噪、异常检测和图像超分辨率等任务中表现出了强大的适应能力，原因在于其可以捕捉和还原输入数据的内在特征和结构。

VAE

理论推导

生成式模型是对联合概率分布进行建模。x表示原始数据，z表示隐变量，先验分布$p(z)\sim \mathcal{N}(0,I)$,
$x|z\sim \mathcal{N}(\mu (z),\sigma (z))$
$p(x)=\int p(x,z)dz=\int p(z)p(x|z)dz$

$$\begin{array}{rl}\log p(x)& =\int q(z|x)\log p(x)dz\\ & =\int q(z|x)\log \left(\frac{p(z,x)}{p(z|x)}\right)dzBayesRule\\ & =\int q(z|x)\log \left(\frac{p(z,x)}{q(z|x)}\frac{q(z|x)}{p(z|x)}\right)dz\\ & =\int q(z|x)\log \left(\frac{p(z,x)}{q(z|x)}\right)dz+\underset{KL(q(z|x)||p(z|x))\ge 0}{\underbrace{\int q(z|x)\log \left(\frac{q(z|x)}{p(z|x)}\right)}}dz\\ & \ge \underset{ELBO,变分下界}{\underbrace{\int q(z|x)\log \left(\frac{p(z,x)}{q(z|x)}\right)dz}}\end{array}$$
极大似然估计，就是为了让$\log p(x)$越大越好，现在我们找到了$\log p(x)$的一个下界，即ELBO，也叫做变分下界。
$$\begin{array}{rl}{L}_b& =\int q(z|x)\log \left(\frac{p(z,x)}{q(z|x)}\right)dz\\ & =\int q(z|x)\log \left(\frac{p(x|z)p(z)}{q(z|x)}\right)dz\\ & =\underset{reconstructionloss}{\underbrace{\int q(z|x)\log p(x|z)dz}}+\underset{-KL(q(z|x)||p(z))\le 0}{\underbrace{\int q(z|x)\log \left(\frac{p(z)}{q(z|x)}\right)dz}}\\ & =E_{q(z|x)}\left[\log p(x|z)\right]-D_{KL}(q(z|x)||p(x|z))\end{array}$$
ELBO经过计算可以分为KL散度+重构Loss.

KL散度：使得 posterior后验分布$q(z|x)$逼近prior先验分布$p(z)$
重构误差：使得原图$x_0$经过Encoder和Decoder后的图片$\tilde{x}$要越接近越好，即MSE(x_0, $\tilde{x}$)

对潜在空间Z的正态分布约束的理解：
相当于加了一个正则项，本来latent z 是不受任何约束的，现在约束它是服从正态分布$\mathcal{N}(0,I)$

变分自编码器关键一点就是增加一个对潜在空间Z的正态分布约束，如何确定这个正态分布就成为主要目标，我们知道要确定正态分布，只要确定其两个参数: 均值$\mu$和标准差$\sigma$。那如何确定 $\mu ,\sigma$呢？用一般的方法或估计比较麻烦效果也不好，研究人员发现**用神经网络去拟合，简单效果也不错。**下图为VAE的架构图：

上图中，模块①的功能把输入样本X通过编码器输出两个m维向量($\mu ,log\_var$), 这两个向量是潜在空间(假设满足正态分布)的两个参数(相当于均值和方差)。那么如何从这个潜在空间采样一个点 Z ?

这里假设潜在正态分布能生成输入图像，从标准正态分布 N(0, 1)中采样一个 $ϵ$(模块②的功能)， 然后使
$$Z=\mu +e^{log\_var/2}\ast ϵ$$
这也是模块③的主要功能。
Z是从潜在空间抽取的一个向量，Z通过解码器生成一个样本$\stackrel{\sim }{X}$, 这是模块④的功能。这里的 $ϵ$ 是随机采样的，这就可以保证潜在空间的连续性，良好的结构性。而这些特性使得潜在空间的每个方向都表示数据中有意义的变化方向。

以上的这些步骤构成整个网络的前向传播过程，那反向传播应如何进行？要确定反向传播就会设计损失函数，损失函数是衡量模型优劣的主要指标。这里我们需要从以下两个方面进行衡量。
1)生成的新图像与原图像的相似度;
2)隐含空间的分布与正态分布的相似度。

度量图像的相似度一般采用交叉熵(如nn.BCELoss) , 度量两个分布的相似度一般采用KL散度(Kullback-Leibler divergence)。这两个度量的和构成了整个模型的损失函数。

以下是损失函数的具体代码，VAE损失函数的推导过程可以参考原论文

# 定义重构损失函数及KL散度
reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)
kl_div = -0.5*torch.sum(1+log_var-mu.pow(2)-log_var.exp())
# 两者相加得总损失
loss = reconst_loss + kl_div

注意：
上面的KL散度损失即
具体可以参看这篇博客讲解
${\mu }_2=0,{\sigma }_2=1$, 这里模型预测出来的$\log \_var$实际上是$\log {\sigma }_1^2$

讲讲为什么是log_var

这里可以看成 log_var = $\log {\sigma }^2=2\log \sigma$，所以$Z=\mu +e^{log\_var/2}\ast ϵ$也就是$$Z=\mu +\sigma \ast ϵ$$
其中$ϵ\sim N(0,1)$, 这里涉及到重参数化reparameterization。

为什么要用重参数化技巧

如果想从高斯分布$N(\mu ,{\sigma }^2)$中采样，可以先从标准分布$N(0,1)$采样出 $ϵ$ , 再得到 $Z=\sigma \ast ϵ+\mu$.
这样做的好处是：

1. 如果直接对$N(\mu ,{\sigma }^2)$进行采样得到Z，则Z无法对$\mu ,\sigma$进行求偏导

2. 将随机性转移到了 $ϵ$ 这个常量上，而 $\sigma$和$\mu$则当做仿射变换网络的一部分,这样得到的$Z=\sigma \ast ϵ+\mu$，则Z就可以对$\mu ,\sigma$进行求偏导来计算损失函数，进行求梯度，进行BP。

用VAE生成图像

下面将结合代码，用pytorch实现，为便于说明起见，数据集采用MNIST，整个网络架构如下图所示。

# 1. 导入必要的包
import os 
import torch 
import torch.nn as nn 
import torch.nn.functional as F 
import torchvision 
from torchvision import transforms 
from torchvision.utils import save_image

# 2. 定义一些超参数
image_size = 784 # 28*28 
h_dim = 400 
z_dim = 20 
num_epochs = 30 
batch_size = 128 
learning_rate = 0.001 

# 如果没有文件夹就创建一个文件夹
sample_dir = 'samples'
if not os.path.exists(sample_dir):
    os.makedirs(sample_dir)
                                     

3. 对数据集进行预处理，如转换为Tensor, 把数据集转换为循环，可批量加载的数据集

# 只下载训练数据集即可
# 下载MNIST训练集
dataset = torchvision.datasets.MNIST(root='./data', train=True, 
                                    transform=transforms.ToTensor(),
                                    download=True)

# 数据加载
data_loader = torch.utils.data.DataLoader(dataset=dataset,
                                    batch_size=batch_size,
                                    shuffle=True)

4. 构建VAE模型，主要由Encoder和Decoder两部分组成

# 定义AVE模型
class VAE(nn.Module):
    def __init__(self, image_size=784, h_dim=400, z_dim=20):
        super(VAE, self).__init__()
        self.fc1 = nn.Linear(image_size, h_dim)
        self.fc2 = nn.Linear(h_dim, z_dim)
        self.fc3 = nn.Linear(h_dim, z_dim)
        
        self.fc4 = nn.Linear(z_dim, h_dim)
        self.fc5 = nn.Linear(h_dim, image_size)

    def encoder(self, x):
        h = F.relu(self.fc1(x))
        return self.fc2(h), self.fc3(h)
    
    # 用mu, log_var生成一个潜在空间点z, mu, log_var为两个统计参数，我们假设
    # 这个假设分布能生成图像
    def reparameterize(self, mu, log_var):
        std = torch.exp(log_var/2)
        eps = torch.randn_like(std)
        return mu + eps * std 

    def decoder(self, z):
        h = F.relu(self.fc4(z))
        return F.sigmoid(self.fc5(h))
    
    def forward(self, x):
        mu, log_var = self.encoder(x)
        z = self.reparameterize(mu, log_var)
        x_reconst = self.decoder(z)
        return x_reconst, mu, log_var 
    

5. 选择GPU和优化器

# 选择GPU和优化器
torch.cuda.set_device(1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = VAE().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

6. 训练模型，同时保存原图像与随机生成的图像

# 训练模型，同时保存原图像与随机生成的图像
for epoch in range(num_epochs):
    for i, (x, _) in enumerate(data_loader):
        # 获取样本，并前向传播
        x = x.to(device).view(-1, image_size)
        x_reconst, mu, log_var = model(x)

        # 计算重构损失和KL散度(KL散度用于衡量两种分布的相似程度)
        # KL散度的计算可以参考https://shenxiaohai.me/2018/10/20/pytorch-tutorial-advanced-02/
        reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)
        kl_div = -0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())

        # 反向传播和优化
        loss = reconst_loss + kl_div 
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if (i+1)%100 == 0:
            print('Epoch [{}/{}], Step [{}/{}], Reconst Loss: {:.4f}, KL Div:{:.4f}'.
                  format(epoch+1, num_epochs, i+1, len(data_loader), reconst_loss.item(), kl_div.item()))

    # 利用训练的模型进行测试
    with torch.no_grad():
        # 保存采样图像，即潜在向量z通过解码器生成的新图像
        # 随机生成的图像
        z = torch.randn(batch_size, z_dim).to(device)
        out = model.decoder(z).view(-1, 1, 28, 28)
        save_image(out, os.path.join(sample_dir, 'sampled-{}.png'.format(epoch+1)))

        # 保存重构图像，即原图像通过解码器生成的图像
        out, _, _ = model(x)
        x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim=3)
        save_image(x_concat, os.path.join(sample_dir, 'reconst-{}.png'.format(epoch+1)))

7. 展示原图像及重构图像

#显示图片
import matplotlib.pyplot as plt 
import matplotlib.image as mpimg 
import numpy as np 

recons_path = './samples/reconst-30.png'
Image = mpimg.imread(recons_path)
plt.imshow(Image)
plt.axis('off')
plt.show()
# reconst
# 奇数列为原图像，欧数列为原图像重构的图像，可以看出重构效果还不错。

8. 由潜在空间通过解码器生成的新图像，这个图像效果也不错

# sampled
# 为由潜在空间通过解码器生成的新图像，这个图像效果也不错
genPath = './samples/sampled-30.png'
Image = mpimg.imread(genPath)
plt.imshow(Image)
plt.axis('off')
plt.show()

总结：这里构建网络主要用全连接层，有兴趣的读者，可以把卷积层，如果编码层使用卷积层(如nn.Conv2d), 则解码器就需要使用反卷积层(如nn.ConvTranspose2d)。

为什么z的均值和方差都是一个20维的向量

z是一个维度为20的一个向量，如果z服从(0,I)高斯分布，那这个高斯分布的mu, sigma应该是什么样的呢？mu, sigma也是一个20维的向量吗？那mu, sigma每一维度的值是什么呢？

当我们说一个向量 $z$ 服从多维标准正态分布（即高斯分布），记作 $z\sim \mathcal{N}(0,I)$，意思是指这个向量的每一个分量都独立地服从标准正态分布。这里具体来说：

• $\mu$ 是分布的均值向量。因为 $z$ 服从 $\mathcal{N}(0,I)$（标准正态分布），所以 $\mu$ 是一个20维的零向量，即 $\mu =[0,0,0,\dots ,0]$。

• $\Sigma$ 是分布的协方差矩阵。在标准正态分布的情况下，这个协方差矩阵是一个单位矩阵 $I$，即 $20\times 20$ 的对角矩阵，对角线上的元素全是1，其余元素全是0。

具体数学表述如下：

• $\mu ={\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\end{array}\right]}_{20\times 1}$
• $\Sigma =I={\left[\begin{array}{ccccc}1& 0& 0& \cdots & 0\\ 0& 1& 0& \cdots & 0\\ 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 1\end{array}\right]}_{20\times 20}$

因此，20维标准正态分布的含义是：

1. 各个分量都有相同的均值 0。
2. 各个分量都有相同的方差 1（标准差也为 1）。
3. 各个分量之间是相互独立的。

这也是为什么这个分布的协方差矩阵是单位矩阵 (I)。

既然是一个协方差矩阵，那为什么VAE在对图像进行训练的时候，Input是一个784维的向量，经过encoder后，出来的是两项，一项为${\mu }_z$,一项为${\sigma }_z$,而且这两项都是20维的向量，为什么啊？既然你上面说“如果 $z$ 服从(0,I)高斯分布，那这个高斯分布的 $\mu$ 是一个20维的向量, ${\Sigma }_z$应该是一个20乘20大小的协方差矩阵”，那为什么神经网络出来的${\sigma }_z$是一个20维的向量呢

这是一个非常好的问题，涉及到变分自编码器（Variational Autoencoder, VAE）的基本原理。让我详细解释一下。

在VAE中，我们希望将输入数据（比如784维的图像向量）通过编码器压缩到一个潜在空间（latent space），并假设潜在变量 ( z ) 服从某种分布（通常是正态分布 (\mathcal{N}(\mu_z, \sigma_z))）来进行生成建模。在训练过程中，我们不是直接对潜在变量 ( z ) 进行建模，而是对其参数 (\mu_z) 和 (\sigma_z) 进行建模。

具体来讲，VAE在编码过程中的步骤如下：

1. 编码器输出参数：编码器接收输入 $\mathbf{x}$（如784维的图像向量），并输出两个20维的向量 ${\mu }_z$ 和 $\log {\sigma }_z^2$, 这里的 ${\mu }_z$ 是潜在变量 $z$ 的均值向量，而$\log {\sigma }_z^2$（对数方差）表达的是每个维度的方差。

2. 重参数化技巧（Reparameterization Trick）：为了能够反向传播并优化模型，我们使用重参数化技巧将潜在变量 $z$ 表示为：
   $z={\mu }_z+{\sigma }_z\odot ϵ$
   其中，$ϵ\sim \mathcal{N}(0,I)$ 是标准正态分布的噪声，$\odot$ 表示元素相乘。这使得我们能够在反向传播时对均值和方差进行优化。

关于为什么 $\Sigma$（协方差矩阵）在这种情况下可以用一个20维的 ${\sigma }_z$ 来表示，是因为我们假设潜在变量 $z$ 的各个维度是独立的，且每个维度都有自己的方差。在这种简化下：

• ${\mu }_z$ 是一个20维的向量，表示潜在变量每个维度的均值。
• ${\sigma }_z^2$（或者 $\log {\sigma }_z^2$，模型输出的是对数方差以确保数值稳定性）是一个20维的向量，表示每个维度的方差。

如果我们用协方差矩阵 $\Sigma$ 表示，这个矩阵是对角形式的，且对角线上的元素是 ${\sigma }_z^2$ 的值。具体来说：
$\Sigma =\text{diag}({\sigma }_z^2)=\text{diag}({\sigma }_{z1}^2,{\sigma }_{z2}^2,\dots ,{\sigma }_{z20}^2)$

上面 ${\sigma }_{zi}^2$ 表示第 $i$ 个潜在变量的方差。因此，对于每个维度 $z_i$，我们有：
$z_i\sim \mathcal{N}({\mu }_{zi},{\sigma }_{zi}^2)$

通过这种方式，编码器输出的是均值向量 ${\mu }_z$ 和对数方差向量 $\log {\sigma }_z^2$，这些参数用来定义潜在空间的每个维度上的独立高斯分布。

那这里是不是进行了简化处理呢？也就是用一个20维的向量sigma来表示协方差的对角线上的值呢？而且这个成立的前提是latent z 的各个维度是相互独立的，每个维度都有自己的方差

是的，正如你所说，VAE中对协方差矩阵进行了简化处理。

具体来说，这种简化包括以下几点：

1. 独立性假设：假设潜在变量 $z$ 的各个维度是独立的。这意味着协方差矩阵 $\Sigma$ 是对角矩阵，而非完全的对称正定矩阵。对于这种对角矩阵，只需要关心对角线上的值（各维度的方差），而不需要考虑非对角线的协方差（各维度之间的相关性）。

2. 对角协方差矩阵：由于各维度独立，因此协方差矩阵 $\Sigma$ 可以表示为对角线上的元素 ${\sigma }_z^2$ 的对角阵：
   $\Sigma =\text{diag}({\sigma }_{z1}^2,{\sigma }_{z2}^2,\dots ,{\sigma }_{z20}^2)$
   这使得我们只需用一个20维向量 ${\sigma }_z^2$
   （或者 $\log ({\sigma }_z^2)$）来表示协方差矩阵，而不是完整的 $20\times 20$ 矩阵。

3. 参数化输出：编码器输出20维的均值向量 ${\mu }_z$ 和20维的对数方差向量 $\log ({\sigma }_z^2)$。对数方差 $\log ({\sigma }_z^2)$ 用于训练的数值稳定性，训练阶段会通过重参数化技巧将其转换为 ${\sigma }_z$：
   $z={\mu }_z+{\sigma }_z\odot ϵ$
   其中，$ϵ$ 是标准正态分布的噪声。

因此，这些假设和处理方式简化了计算和模型复杂度，但仍能有效地学习潜在空间的分布和结构。你提到的成立前提是正确的：这基于 $z$ 的各个维度是相互独立且每个维度都有自己的方差。尽管这种独立性假设有时可能不完全符合实际数据的潜在结构，但在实践中，这种简化通常能够得到不错的结果，且计算更为高效。

如果不做简化处理，协方差矩阵就会非常复杂，尤其对于高维度数据，生成和优化 $\Sigma$ 将会变得十分困难。因此，对角化协方差矩阵是一种常用且有效的简化方法。

VAE和Gaussian混合模型的关系

那我重新来理解一下，实际上这个z可以理解为由20个服从高斯分布的一维变量的高斯混合模型？

虽然高斯混合模型（Gaussian Mixture Model, GMM）和我们在变分自编码器（VAE）中看到的潜在变量并不是完全相同的概念，但你提到了一个有趣且有助于理解的类比。我们可以通过在一些层面上的类比来进一步理解这两种模型。

高斯混合模型 (GMM)

GMM是一种聚类模型，其中数据被视为由若干个高斯分布（成分）混合而成。每个数据点可以看作是由某一个高斯成分生成的。

• GMM的每个成分有其自己的均值向量和协方差矩阵。
• 数据点的生成过程包括从成分分布中选择一个成分，然后从该成分的高斯分布中生成数据点。

VAE的潜在变量 $z$

在VAE中，只假定潜在变量 $z$ 服从某个多维正态分布（常见的是标准正态分布 $\mathcal{N}(0,I)$），并使用这些变量进行生成建模。

• 在编码阶段，我们通过神经网络将输入数据 $x$ 编码为均值向量 ${\mu }_z$和对数方差向量 $\log {\sigma }_z^2$。
• 使用这些均值和方差构成一个高维正态分布 $\mathcal{N}({\mu }_z,\text{diag}({\sigma }_z^2))$ 来对潜在变量 $z$ 进行建模。

类比理解

虽然VAE中的每个维度（或变量）$z_i$ 是独立且服从一维高斯分布的，这种方式类似于将总的潜在变量 $z$ 看作是由独立的高斯成分构成的一个形式。以下是进一步的类比：

• 独立高斯成分：在VAE的简化处理下，可以认为潜在变量 $z$ 的每个维度$z_i$ 是一个独立的一维高斯分布。
• 独立性假设：这种方式实际上假设潜在空间的各个维度彼此独立。这与GMM假设数据点间生成的独立性略有区别。

是否为高斯混合模型？

严格来说，VAE的潜在变量分布并不是一个标准意义上的高斯混合模型，因为GMM涉及多个成分的高斯分布并带有权重，而VAE的潜在变量分布是一个单独的多维正态分布。

但是，可以通过独立成分的角度理解成：

• 潜在变量 $z$ 的分布可以看作由多个独立的一维高斯分布构成，每个维度对应一个独立的高斯分布。
• 这些独立的高斯分布共同构成了一个更高维度的联合分布，这个分布仍然是高斯分布，但在独立性假设下其协方差矩阵是对角矩阵。

总结

尽管不完全是一个高斯混合模型，VAE中对潜在变量的独立性简化处理确实让我们可以以独立高斯分布的视角来看待每一个维度。这种简化处理使得计算和模型训练更为便捷，同时也保留了潜在变量建模的有效性。

那实际上这个z可以理解为由20个服从高斯分布的一维变量的组合吗？

是的，你可以这样理解。具体来说，在变分自编码器（VAE）的设定中，潜在变量 $z$ 通常被建模为一个多维的高斯分布，并且在简化处理的情况下，假设它的各个维度是独立的。那么这个多维高斯分布实际上就是由若干个一维的高斯分布组合而成的。

具体解释

1. 多维高斯分布：潜在变量 $z$ 通常被建模为一个 $d$ 维的高斯分布，假设 $d=20$。这种高斯分布包含一个均值向量 ${\mu }_z$ 和一个协方差矩阵 $\Sigma$。

$z\sim \mathcal{N}({\mu }_z,\Sigma )$

2. 独立性假设：简化处理通常假设各维度是独立的，这意味着协方差矩阵 $\Sigma$ 是一个对角矩阵。在这种情况下，$\Sigma$ 可以表示为对角线上的方差（或标准差）：

$\Sigma =\text{diag}({\sigma }_{z1}^2,{\sigma }_{z2}^2,\dots ,{\sigma }_{z20}^2)$

3. 一维高斯分布的组合：因为协方差矩阵是对角的，潜在变量 $z=(z_1,z_2,\dots ,z_{20})$ 的每个维度 $z_i$ 都独立地服从于自己的高斯分布：

$z_i\sim \mathcal{N}({\mu }_{zi},{\sigma }_{zi}^2)$

因此，整个 $z$ 可以看成是由20个独立的一维高斯分布组合成的一个向量。

举例说明

假设我们的潜在变量 $z$ 是一个20维的向量：

$z=(z_1,z_2,\dots ,z_{20})$

对于每一个 $z_i$，我们有：

$z_i\sim \mathcal{N}({\mu }_{zi},{\sigma }_{zi}^2)$

其中，${\mu }_{zi}$ 是第 $i$ 个维度的均值，${\sigma }_{zi}^2$ 是第 $i$ 个维度的方差。

在编码过程中，我们使用神经网络来预测均值向量 ${\mu }_z=({\mu }_{z1},{\mu }_{z2},\dots ,{\mu }_{z20})$ 和对数方差 $\log ({\sigma }_z^2)=(\log ({\sigma }_{z1}^2),\log ({\sigma }_{z2}^2),\dots ,\log ({\sigma }_{z20}^2))$。在重参数化技巧中，我们生成每个 $z_i$：

$z_i={\mu }_{zi}+{\sigma }_{zi}\cdot {ϵ}_i$

其中，${ϵ}_i$ 是从标准正态分布 $\mathcal{N}(0,1)$ 中采样的随机噪声。

总结

是的，潜在变量 $z$ 可以理解为由20个服从高斯分布的一维变量的组合。每一个维度都是一个独立的高斯分布，简化了整体的建模和计算复杂度。这种方法使得模型在训练和生成过程中更加高效，同时仍然保留了对数据生成分布的有效建模。

VAE实际上是一个高斯混合模型，这句话怎么理解呢？是因为z是一个连续的变量吗？所以可以将其理解为一个高斯混合模型？

把VAE称为高斯混合模型（Gaussian Mixture Model, GMM）并不完全准确，因为它们本质上是不同的模型和方法。然而，如果你在某些方面将两者类比，这是可以理解的。让我们更详细地讨论这个类比，并了解为什么和在什么程度上可以这样理解。

高斯混合模型 (GMM)

GMM是一种生成模型，它假设数据点是从几个高斯分布中采样而来的，每个高斯分布被称为一个“成分”。

• 每个成分都有自己的均值向量和协方差矩阵。
• 每个数据点的生成过程包括从多个高斯成分中选择一个（根据成分的权重），然后从选择的成分高斯分布中生成数据点。

变分自编码器 (VAE)

VAE也是一种生成模型，它使用潜在变量（latent variables）来建模数据生成过程。

• 在VAE中，潜在变量 ( z ) 通常被假设为多维标准正态分布 (\mathcal{N}(0, I))。
• 在编码过程中，输入数据 ( x ) 被编码成潜在变量 ( z ) 的分布参数（均值向量 (\mu_z) 和对数方差向量 (\log \sigma^2_z)）。
• 使用重参数化技巧，从上一步得到的分布中采样 ( z )，然后通过解码网络将 ( z ) 转化回数据空间以生成数据样本 (\tilde{x})。

类比理解

尽管VAE和GMM有不同的具体实现和理论基础，你提到了一些使得 VAE 被类比为 GMM 的理由：

1. 潜在空间的连续变量：在VAE中，潜在变量 ( z ) 是一个连续变量，通常被假设为多维正态分布。GMM中，每个成分代表一个高斯分布，而在 VAE 中，我们可以认为整个潜在空间中不同的区域代表了不同的高斯分布。
2. 隐变量的分布：在某种程度上，可以将VAE中的潜在空间理解为由连续变化的高斯分布所构成。虽然这些高斯分布并不明确地分为几个成分，但由于潜在空间的连续性以及通过神经网络编码和解码的非线性变换，它们近似地表示了一种复杂的、由高斯分布混合成的生成机制。

为什么 VAE 不是标准意义的 GMM

• 成分数量：GMM中成分数量是固定并且明确的（每个成分都有一个权重），而VAE的潜在空间是连续的，并没有固定数量的成分划分。
• 生成过程：GMM中，数据点是通过选择一个特定的高斯成分并从中采样生成的，而在VAE中，数据通过从潜在空间中采样潜在变量 ( z )，然后通过解码网络生成。

总结

VAE并不是严格意义上的高斯混合模型（GMM），但是可以在某些方面与GMM进行类比理解：

• 潜在变量 ( z ) 被看作是从高斯分布采样。
• 生成数据的过程涉及从高斯分布中采样，将潜在变量映射回数据空间的过程类似于从多个潜在的高斯成分中进行采样和生成。

通过这种类比，你可以更直观地理解VAE中的潜在空间和数据生成过程，但要记住这仅仅是类比，VAE和GMM在模型假设、具体实现和应用上还有明显的不同。

那可以理解为VAE是一个有无限个成分的高斯混合模型吗？因为latent z 是一个连续的变量

这种理解在某种程度上是成立的，但需要一些谨慎。你可以将VAE看作是一种具有无限成分的隐式高斯混合模型（GMM），这种解释在对潜在空间的理解上是有帮助的。让我们深入探讨这个类比的合理性及其限制。

潜在空间的无限成分类比

1. 连续的潜在空间：

   • 在VAE中，潜在变量 ( z ) 是一个连续变量，通常假设其服从标准正态分布 ( \mathcal{N}(0, I) )。
   • 这种连续性意味着，潜在空间中每一个点都代表一种潜在的“状态”或“成分”，从而使得你可以认为潜在空间是由无限多个成分所构成的。

2. 隐含的高斯成分：

   • 每个潜在变量 ( z ) 对应的高斯分布（在编码过程中通过均值和方差参数）可以被视作隐含的高斯成分。
   • 当你从潜在空间中采样一个 ( z )，并通过解码器生成数据样本时，可以看作是从无限多个高斯成分中选择了一个进行采样和生成。

3. 生成机制的类比：

   • 在GMM中，你明确地选择一个成分并从中生成数据。
   • 在VAE中，从标准正态分布中采样 ( z ) 并将其通过解码器是隐含的选择和生成过程。

为什么这种类比有用？

这种类比帮助你理解VAE的生成过程，特别是它如何通过连续的潜在空间实现复杂的数据分布。你可以想象，VAE类似于一个极其复杂且具有无限成分的高斯混合模型，它利用神经网络的非线性能力从潜在空间生成多样化的数据。

需要注意的几点

虽然这种类比有助于理解，但需要注意以下几点以避免混淆：

1. 成分的明确性：

   • 在标准的GMM中，成分数量是明确的且有限的，每个成分有一个明确的权重。
   • 在VAE中，没有明确数量的成分划分，只是隐含地存在着无限多的“状态”。

2. 生成过程的机制：

   • GMM明确地选择成分，而在VAE中，生成过程并不明确地区分成分，而是通过对潜在空间的连续采样和非线性变换进行数据生成。

3. 模型结构和训练目标：

   • GMM和VAE有不同的模型结构和训练目标。GMM通过最大似然估计进行参数学习，而VAE通过变分推断最大化证据下界（ELBO）进行训练。

总结

可以在某种程度上将VAE理解为具有无限成分的隐式高斯混合模型，因为它通过潜在变量 ( z ) 的连续分布进行数据生成。这种类比在理解VAE的潜在空间和生成机制上是有帮助的。然而，要记住这只是类比而非严格等价的描述，因为VAE和GMM在模型假设、结构和训练方法上有显著的不同。

那比如对于cifar10,对于数字0和数字1，2 的图片，那不同的数字，都约束他们的latent z去逼近(0,1),那模型在生成的时候，它怎么能生成多样性的呢？它怎么能生成出来不同的数字呢？他们的latent z的分布约束都是正态分布唉

这确实是一个有趣的问题，涉及到如何理解变分自编码器（VAE）在处理类别标签和潜在空间中的复杂关系。虽然VAE中的潜在变量 ( z ) 被约束为符合标准正态分布 (\mathcal{N}(0, I))，但模型能够生成多样化的数据样本以及不同类别的原因有以下几点：

1. 潜在空间的结构和分布

虽然潜在变量 ( z ) 总体上被约束为标准正态分布，但在实际应用中，不同类别的样本在潜在空间中会形成不同的聚簇。这是因为，即使最终的潜在变量分布是标准正态分布，不同类别的样本在经过编码器编码到潜在空间时，仍然会体现出某种结构或模式。

2. 生成的多样性

生成数据的多样性主要来自于以下几个方面：

• 潜在变量的不同值：尽管 ( z ) 的分布被约束为标准正态分布，不同潜在变量的取值仍然能反映出数据的多样性。例如，对于同一类别的图片（如数字0），潜在变量 ( z ) 的特定值会捕捉到不同的变换和细节，如不同的字体、角度和背景噪声等。
• 解码器的复杂性：解码器是一个强大的神经网络，能够将同一个潜在空间中的小差异放大到数据空间中的显著差异。这使得即使潜在变量 ( z ) 的变化微小，生成的数据也能具有很大的多样性。

3. 类别信息的隐含编码

在标准的VAE中，类别信息并没有显式地使用。但如果你希望更好地控制生成数据的类别，可以采用一些变体来显式或隐式地使用类别信息：

• 带有条件信息的VAE (Conditional VAE, CVAE)：在CVAE中，我们不仅将数据 ( x ) 编码到潜在变量 ( z )，还将类别标签 ( y ) 作为条件信息输入到编码器和解码器中。这允许模型学习到潜在空间中的特定区域对应特定的类别。
• 离散潜在变量模型：有些模型通过引入离散潜在变量来显式地表示类别信息。例如，Gumbel-Softmax VAE可以在潜在空间中使用离散的类别变量。

4. 训练过程中的自组织

即使是在标准的VAE中，不同类别的数据样本在经过训练过程后，潜在空间中的编码通常会自动形成一定的组织结构。例如，对于CIFAR-10中的不同数字，不同数字的图像在潜在空间中往往会形成不同的聚簇。尽管这些聚簇不是明确划分的，各类别之间的边界也可能是模糊的，但这种自组织现象使得生成多样化和不同类别的样本成为可能。

实际示例

假设在处理CIFAR-10中的数字0和数字1的图像，即使我们最终得到的潜在变量分布是标准正态分布，不同数字的图像在潜在空间中会形成自己的分布模式。例如，“0”的图像可能更多地集中在潜在空间的某些区域，而“1”的图像可能在其他区域。这样，当你从潜在空间中采样值并通过解码器生成图像时，能够通过不同的潜在变量生成具有不同特征和细节的图像。

总结

尽管VAE中的潜在变量 ( z ) 总体上被约束为标准正态分布，但模型能够通过编码器和解码器的复杂性和灵活性，捕捉到数据的多样性和类别信息。在潜在空间中，不同类别的样本会形成自己的聚簇结构，这种结构让模型能够生成不同类别和多样化的样本。对于更明确地控制类别，可采用条件VAE或其他变体模型。

也就是说，在对z进行采样的时候，采样出来的z不是完全的(0,1)分布的，因为它还要加一些噪声，而这个噪声的稍微不同，就会使得生成的样本不一样，是这样吗？

你的理解方向是对的，但是我们需要更精确地描述一下 VAE 中 (z) 的采样过程和噪声的作用。

潜在空间与噪声的角色

编码过程中的潜在变量

1. 编码器输出的分布：

   • VAE 的编码器将输入数据 (x) 映射到潜在空间，输出的是潜在变量 (z) 的分布参数：均值 (\mu(x)) 和方差 (\sigma^2(x)) 或标准差 (\sigma(x))。
   • 这意味着，给定输入数据 (x)，编码器实际上定义了一个条件高斯分布 ( \mathcal{N}(\mu(x), \sigma^2(x)) )。

2. 重新参数化技巧：

   • 为了能够进行反向传播，VAE 使用了重新参数化技巧。
   • 具体来说，从 ( \mathcal{N}(\mu(x), \sigma^2(x)) ) 中采样一个潜在变量 (z) 被分解为从标准正态分布 ( \mathcal{N}(0, 1) ) 中采样噪声 (\epsilon)，然后通过 (\mu(x) + \sigma(x) \cdot \epsilon) 得到最终的 (z)。
   • 这里的噪声 (\epsilon) 是关键，因为它引入了随机性。

解码过程中的生成

1. 潜在空间的采样：
   • 在生成数据时，我们从标准正态分布 ( \mathcal{N}(0, I) ) 中采样潜在变量 (z)。
   • 每一个采样的 (z) 值，尽管来自标准正态分布，但由于方差和均值的影响，最终通过解码器生成的数据样本会有较大差异。

多样性和类别分布

尽管潜在空间中的变量 (z) 总体上是被约束为标准正态分布，但是：

• 对于每个数据样本 (x)，编码器输出的 (\mu(x)) 和 (\sigma(x)) 会不同，因此采样的 (z) 也会形成各自的分布。
• 对于同一类别的不同样本，编码器的输出分布会有一些重叠，这让不同的 (z) 值依然能够生成多样的样本。

噪声带来的多样性

正如你提到的，噪声在 VAE 中扮演了至关重要的角色：

1. 编码过程中的噪声：

   • 噪声 (\epsilon) 是从标准正态分布中采样的，其稍微不同即可导致最终的 (z) 不同。
   • 这导致了在解码阶段，从这些稍有差异的 (z) 中生成不同的数据样本。

2. 解码过程中的非线性变换：

   • 解码器是一个非线性神经网络，即使 (z) 的差异很小，经过解码器的复杂非线性变换后，最终生成的数据样本可能差异很大。
   • 这放大了潜在变量空间中的小变动，带来了生成样本的多样性。

总结

是的，你的理解是对的。从标准正态分布 ( \mathcal{N}(0, 1) ) 中采样噪声 (\epsilon)，并通过 (\mu(x) + \sigma(x) \cdot \epsilon) 能够得到不同的 (z)，即使这些差异非常小，通过解码器生成的数据样本也会不同。噪声引入的随机性与解码器的非线性变换共同作用，实现了 VAE 生成数据的多样性和复杂性。

整体上，虽然 (z) 来源于一个标准正态分布，但通过编码器的条件高斯分布和再参数化技巧，引入的噪声 (\epsilon) 使得每次采样的 (z) 具备多样性，从而解码器生成的样本也多样化。

“即使是在标准的VAE中，不同类别的数据样本在经过训练过程后，潜在空间中的编码通常会自动形成一定的组织结构。例如，对于CIFAR-10中的不同数字，不同数字的图像在潜在空间中往往会形成不同的聚簇。尽管这些聚簇不是明确划分的，各类别之间的边界也可能是模糊的，但这种自组织现象使得生成多样化和不同类别的样本成为可能。”你手它会生成不同的聚簇，那怎么进行可视化呢？怎么证明它确实会生成不同的聚簇呢？

要验证和可视化 VAE 的潜在空间中是否形成了聚簇，可以采用以下几种方法：

方法一：二维或三维可视化

1. 降维方法：

   • t-SNE（t-distributed Stochastic Neighbor Embedding）：一种降维算法，适合于高维度数据的非线性降维，并很好地保留局部邻近关系。在二维或三维空间中可视化潜在变量 (z)。
   • PCA（Principal Component Analysis, 主成分分析）：线性降维技术，可以将高维数据映射到低维空间（如二维或三维）进行可视化。

2. 可视化过程：

   • 捕获一批数据集（如 CIFAR-10）中的样本，通过训练好的编码器获得其潜在变量 (z)。
   • 使用 t-SNE 或 PCA 对这些潜在变量 (z) 进行降维到二维或三维空间。
   • 对降维后的数据进行绘图（用不同的颜色代表不同的类别）。

下面是一个简单的Python示例，假设我们已经有了数据集的潜在变量 (z)：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA

# 假设 z_vals 是由编码器输出的潜在变量，labels 是对应的类别标签
# z_vals 形状为 (num_samples, latent_dim)
# labels 形状为 (num_samples,)

z_vals = ...  # 获取编码器输出的潜在变量
labels = ...  # 对应的数据标签

# 使用 t-SNE 将潜在变量降维到2D
tsne = TSNE(n_components=2)
z_tsne = tsne.fit_transform(z_vals)

# 使用 PCA 将潜在变量降维到2D
pca = PCA(n_components=2)
z_pca = pca.fit_transform(z_vals)

# 绘制降维后的数据点，按类别进行颜色标注
def plot_embedding(z_embedded, title):
    plt.figure(figsize=(8, 8))
    for i in range(10):  # 假设有10个类别
        indices = labels == i
        plt.scatter(z_embedded[indices, 0], z_embedded[indices, 1], label=str(i))
    plt.legend()
    plt.title(title)
    plt.show()

plot_embedding(z_tsne, "t-SNE visualization of latent space")
plot_embedding(z_pca, "PCA visualization of latent space")

方法二：类内分布的统计分析

• K-means 聚类：在潜在空间上进行 K-means 聚类，然后分析每个聚类中心周围点的类别标签分布。如果不同类别在潜在空间上形成了不同的聚簇，则我们预期在同一个聚类中心附近的点会有相似的类别标签。

方法三：交叉验证生成样本

• 类条件生成：将潜在空间中的点空间按照其类别标签进行采样，然后通过解码器生成数据。检查生成的数据的类别是否一致，可以进一步验证是否形成了聚簇。

实验验证示例

假设我们用 CIFAR-10 数据集和训练好的 VAE 模型测试：

import torch
import torchvision
from torchvision import datasets, transforms
from torch.utils.data import DataLoader

# 加载CIFAR-10数据集
transform = transforms.Compose([
    transforms.ToTensor(),
])
cifar10_data = datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
data_loader = DataLoader(cifar10_data, batch_size=128, shuffle=False)

# 提取潜在变量 z
z_vals = []
labels = []
vae = ...  # 假设这是我们训练好的 VAE 模型

for images, label in data_loader:
    with torch.no_grad():
        images = images.to(device)
        mu, logvar = vae.encoder(images)
        z = vae.reparameterize(mu, logvar)
        z_vals.append(z.cpu().numpy())
        labels.append(label.cpu().numpy())

z_vals = np.concatenate(z_vals, axis=0)
labels = np.concatenate(labels, axis=0)

# 可视化
plot_embedding(z_vals, labels, method='tsne')

通过上述方法中的可视化步骤和验证步骤，可以直观地观察到VAE潜在空间中的数据分布，验证各类数据是否形成了类似聚簇的结构。 主要依据就是在降维后的空间中，不同类别的数据点会有较为明显的聚