微积分基础之图形面积(体积)计算
一、平面图形面积
积 分 的 要 领 1 : 以 长 方 形 为 基 础 来 思 考 \boxed{积分的要领1:以长方形为基础来思考} 积分的要领1:以长方形为基础来思考
1、简单图形的面积
(1)长方形
长
×
\times
×宽,不会的请离开
(2)三角形
底
×
\times
×高/2,不会的请离开
(3)平行四边形
底
×
\times
×高,不会的请离开
(4)梯形
(
(
(上底
+
+
+下底
)
×
)\times
)×高/2,不会的请离开
2、稍微复杂一点的图形面积
积 分 的 要 领 2 : 把 图 形 看 作 小 长 方 形 的 组 合 \boxed{积分的要领2:把图形看作小长方形的组合} 积分的要领2:把图形看作小长方形的组合
(1)圆
法1:
用圆规在方格纸上画一个圆,接着数一数圆中的方格数
我在边长为
1
m
m
1mm
1mm的方格纸上画了一个半径为
2
c
m
2cm
2cm的圆,我算(shǔ)出圆中共有
1189
1189
1189个格子,所以我们算出的圆周率是
2.9725
2.9725
2.9725
虽然这个误差很大,但是,随着格子边长的缩小,我们的准确度就越高
法2:
有什么办法可以提高精度吗?有,如图,我们把圆分成细长的小条来求由于我太懒了,所以只画了3条
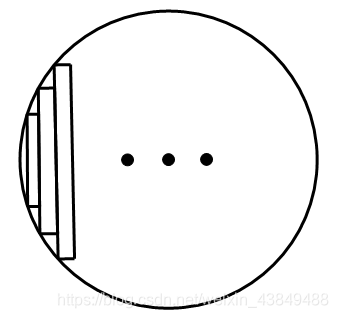
每一个小条的宽度是
Δ
x
\Delta x
Δx,表示非常小的数值
这样,我们可以得出圆的面积
=
∫
左
端
右
端
短
条
在
x
值
对
应
的
长
度
d
x
=\int_{左端}^{右端}短条在x值对应的长度dx
=∫左端右端短条在x值对应的长度dx
d
x
dx
dx可以理解为
lim
Δ
x
→
0
Δ
x
\lim \limits_{\Delta x \rightarrow 0}\Delta x
Δx→0limΔx
我做了一个实验,计算半径为
1
c
m
1cm
1cm的圆,把它分成
N
N
N个小条,制成一张表格
| N N N | 所有小条的总面积 |
|---|---|
| 10 10 10 | 2.637049 2.637049 2.637049 |
| 20 20 20 | 2.904518 2.904518 2.904518 |
| 40 40 40 | 3.028465 3.028465 3.028465 |
| 200 200 200 | 3.120417 3.120417 3.120417 |
| 2000 2000 2000 | 3.139555 3.139555 3.139555 |
| 20000 20000 20000 | 3.141391 3.141391 3.141391 |
可见 N N N越来越大时,小条的总面积就会越接近圆的面积 π r 2 \pi r^{2} πr2
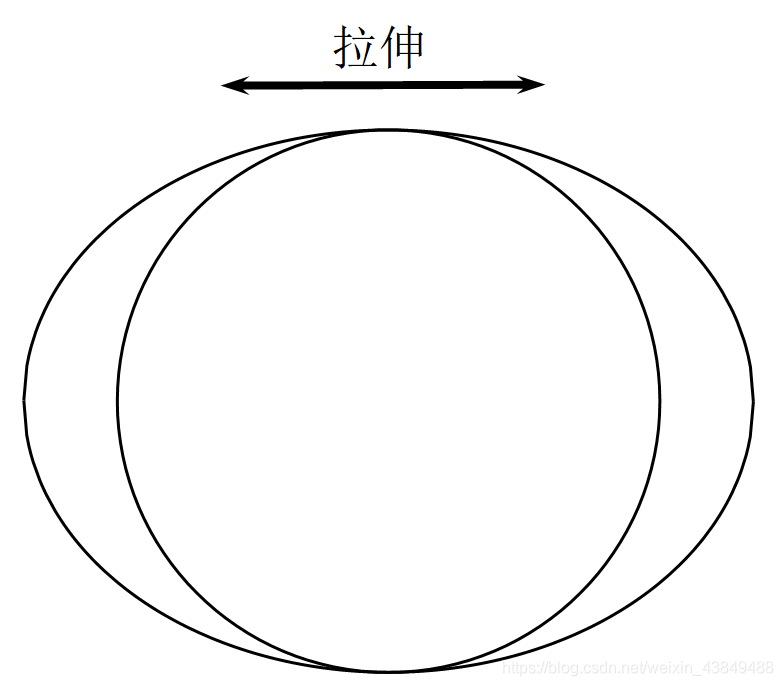
椭圆
椭圆是由圆拉伸来的,所以我们也可以把它分成细长的短条来求,这个小条的面积就是圆的小条面积的
a
b
\frac{a}{b}
ba倍,所以,椭圆的面积就是
π
a
b
\pi ab
πab
积
分
的
要
领
3
:
把
图
形
分
解
成
长
方
形
然
后
进
行
伸
缩
变
换
\boxed{积分的要领3:把图形分解成长方形然后进行伸缩变换}
积分的要领3:把图形分解成长方形然后进行伸缩变换
立体图形表面积和体积
祖暅定理
积
分
的
要
领
4
:
把
图
形
看
作
被
切
割
后
的
组
合
\boxed{积分的要领4:把图形看作被切割后的组合}
积分的要领4:把图形看作被切割后的组合
在外国称作卡瓦列利原理
截面面积总是相等的两个立体图形,体积也相等
三分之一之谜
积
分
的
要
领
5
:
灵
活
应
用
祖
暅
定
理
\boxed{积分的要领5:灵活应用祖暅定理}
积分的要领5:灵活应用祖暅定理
大家都知道圆锥的体积公式吧?体积
=
=
=底面积
×
\times
×高
×
1
3
\times\frac{1}{3}
×31
话说这个
1
3
\frac{1}{3}
31是哪来的?
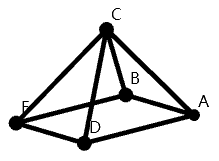
首先,我们从四棱锥说起
我们先把C点平移到A的正上方,使得
A
C
⊥
AC\perp
AC⊥平面
A
B
D
ABD
ABD(祖暅定理)
⇓
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Downarrow
⇓
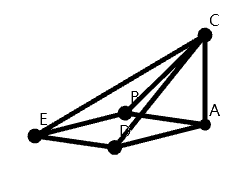
这时,我们发现3个这样的椎体可以拼成一个长方形,因此,我们可以得到这个四棱锥的体积就是
1
3
×
\frac{1}{3}\times
31×底面积
×
\times
×高
得到了四棱锥的体积之后,我们就可以计算任意椎体的体积了
我们把椎体的底面分成许多很小的长方形,所以每一个小四棱锥的体积相加就是椎体的体积了,也就等于
1
3
×
\frac{1}{3}\times
31×底面积
×
\times
×高
球的体积
我们先做出一个立体图形,我把它称为钵体,它是一个圆柱再去掉一个圆锥后的图形
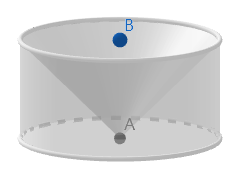
我们可以发现,它的每一个截面的面积和一个半球上的截面的面积相同,所以,根据祖暅定理,我们可以知道,球的体积
=
2
×
2
3
π
R
3
=
×
4
3
π
R
3
=2\times\frac{2}{3}\pi R^3=\times\frac{4}{3}\pi R^3
=2×32πR3=×34πR3
积
分
的
要
领
6
:
寻
找
“
有
效
的
对
应
、
关
系
条
件
”
\boxed{积分的要领6:寻找“有效的对应、关系条件”}
积分的要领6:寻找“有效的对应、关系条件”
球的表面积
积
分
的
要
领
7
:
相
比
“
纠
结
于
细
节
”
,
“
如
何
思
考
才
能
顺
利
计
算
”
更
优
先
\boxed{积分的要领7:相比“纠结于细节”,“如何思考才能顺利计算”更优先}
积分的要领7:相比“纠结于细节”,“如何思考才能顺利计算”更优先
我们把球的表面分成许多小的四棱锥,所以,我们可以得到球的体积
=
1
3
×
R
×
=\frac{1}{3}\times R\times
=31×R×球的表面积
所以,我们可以得到球的表面积
=
4
π
R
2
=4\pi R^2
=4πR2
终极问题——甜甜圈的体积
大家都知道甜甜圈吧?

我用软件画了一个甜甜圈,我们假设甜甜圈边上的圆心到中心的距离为
4
c
m
4cm
4cm,半径为
2
c
m
2cm
2cm,我们尝试水平切割,我们就可以得到一个个圆环
这些圆环的外圈的半径
=
4
+
4
−
x
2
=4+\sqrt{4-x^2}
=4+4−x2,内圈的半径
=
4
−
4
−
x
2
=4-\sqrt{4-x^2}
=4−4−x2,所以这个截面的面积
=
16
π
4
−
x
2
=16\pi\sqrt{4-x^2}
=16π4−x2(
x
x
x代表到圆心的距离)
由此,我们就可以表示出整个甜甜圈的体积就是
∫
−
2
2
16
π
4
−
x
2
d
x
\int_{-2}^{2}16\pi\sqrt{4-x^2}dx
∫−2216π4−x2dx这个积分是在不需要我们计算,我们只要画一个图就行了
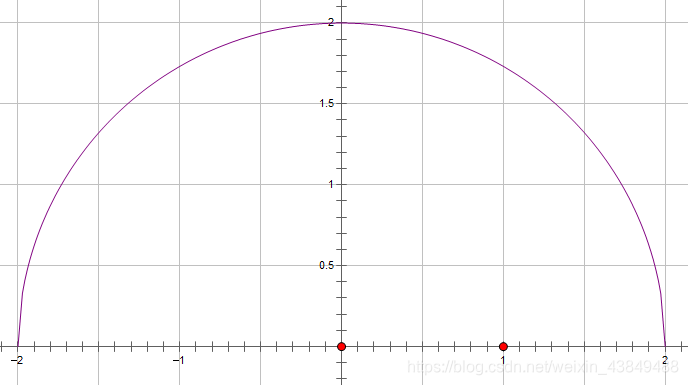
积分相当于计算这个图形的面积,所以也就是
∫
−
2
2
16
π
4
−
x
2
d
x
=
16
π
×
2
π
=
32
π
2
\int_{-2}^{2}16\pi\sqrt{4-x^2}dx=16\pi\times2\pi=32\pi^{2}
∫−2216π4−x2dx=16π×2π=32π2
参考材料:
《简单微积分》神永正博 著





 本文介绍了微积分基础知识,讲解了如何计算平面图形如长方形、三角形、平行四边形和梯形的面积,以及通过圆、椭圆的面积计算深入理解积分概念。此外,探讨了立体图形的表面积和体积,包括应用祖暅定理解决体积问题,并解析了球体体积和表面积的积分计算方法。最后,通过甜甜圈体积的计算展示了积分在实际问题中的应用。
本文介绍了微积分基础知识,讲解了如何计算平面图形如长方形、三角形、平行四边形和梯形的面积,以及通过圆、椭圆的面积计算深入理解积分概念。此外,探讨了立体图形的表面积和体积,包括应用祖暅定理解决体积问题,并解析了球体体积和表面积的积分计算方法。最后,通过甜甜圈体积的计算展示了积分在实际问题中的应用。
















 5363
5363

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








