图像的变换——dwt、idwt、wcodemat、dwt2、idwt2、wavedec2、waverec2

图像小波变换

一、一维小波变换

1. dwt函数

功能： 单级一维离散小波变换
句法：

• [cA,cD] = dwt(x,wname)
  使用小波’wname’对信号X进行单层分解，求得的近似系数存放在数组cA中，细节系数存放在数组cD中
• [cA,cD] = dwt(x,LoD,HiD)
  分别使用指定的低通和高通滤波器计算小波分解
• [cA,cD] = dwt(…,‘mode’,extmode)
  使用指定的扩展模式计算小波分解。MODE是包含扩展模式的字符串。

代码示例：

%装载一维原始信号 
load noissin;%带噪声的正弦信号   
s=noissin(1:1000); %取信号的前1000个采样点
%画出原始信号的波形 
subplot(411);plot(s);  %函数subplot的作用是在标定位置上建立坐标系 
title('原始信号'); 
%下面用haar小波函数进行一维离散小波变换 
[ca1,cd1]=dwt(s,'haar'); 
subplot(4,2,3);plot(ca1); axis tight;%自动设置x轴和y轴的范围使图形区域正好占满整个显示空间
ylabel('haar(ca1)'); 
subplot(4,2,4);plot(cd1); axis tight;
ylabel('haar(cd1)'); 
%给定一个小波db2,计算与之相关的分解滤波器 
[Lo_D,Hi_D]=wfilters('db2','d'); 
%用分解滤波器Lo_D,Hi_D计算信号s的离散小波分解系数 
[ca2,cd2]=dwt(s,Lo_D,Hi_D); 
subplot(4,2,5);plot(ca2); axis tight;
ylabel('db2(ca2)'); 
subplot(4,2,6);plot(cd2); axis tight;
ylabel('db2(cd2)');

结果显示：

代码示例：

load noissin;  %装载信号 
s=noissin(1:1000); 
ls=length(s);  %计算信号点的个数ls 
%对s进行一维连续小波变换，把返回系数存到矩阵w中 
w=cwt(s,[12.12,10.24,15.48,1.2,2:2:10],'db3','plot');   
xlabel('时间'); 
ylabel('变换尺度'); 
title('对应于尺度a=12.12,10.24,15.48,1.2,2,4,6,8,10小波变换系数的绝对值');

结果显示：

2.idwt函数

功能： 单级逆离散一维小波变换
句法：

• x = idwt(cA,cD,’wname‘)
  返回基于近似和细节系数向量CA和CD，并使用小波“wname”的单层重构近似系数向量X

代码示例：

load noisdopp;% 装载信号
[A,D] = dwt(noisdopp,'sym4');%使用Symlet(symN)小波
x = idwt(A,D,'sym4');
max(abs(noisdopp-x))

运行结果：

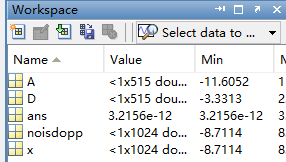
• x = idwt(cA,cD,LoR,HiR)
  如上所述，使用指定的过滤器进行重建：
  LoR是重构低通滤波器。
  HiR是重建高通滤波器。
  LoR和HiR的长度必须相同。

代码示例：

load noisdopp;