平面三角形单元有限元实现——有限元实践笔记（5）

引言

对于空间实体微元，应力状态如下图所示，由三个方向的正应力和三个方向的剪应力组成，正应力垂直于微元表面，剪应力在微元表面内。

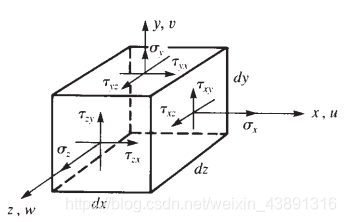
剪应力互等定理

因此对于空间问题，应力的独立分量有6个

三维问题的求解相对复杂，有时可根据分析问题的特点对其进行适当简化，如简化为平面应力问题或平面应变问题，平面应力问题和平面应变问题都是二维问题，求解相对简单，二维问题的有限元求解需要用到二维单元，即面单元。
本文利用平面三角形单元离散平面结构，给出平面问题的有限元求解的一般过程。
本文由以下几个部分组成：

• 平面应力和平面应变基本概念
• 二维应力应变状态
• 平面三角形单元的刚度矩阵和方程的推导
• 平面结构的有限元分析实例及matlab代码

1 平面应力和平面应变基本概念

平面应力问题
平面应力是指所有的应力都在平面内，对于薄板结构，即板厚远小于结构的另外两个尺度，只承受面内载荷，例如下图所示平板，在xy平面内右侧受到拉力T的作用，假定此时垂直于平面的法向应力和剪切应力为0，此时问题得到简化。

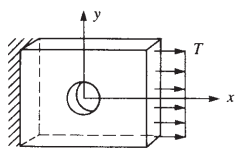
所有厚度方向的应力为0

平面应变问题
类似的可定义平面应变问题，平面应变状态为所有长度方向的应变为0，典型结构为等截面的细长体，如下图所示，只承受xy平面内的载荷，且载荷沿长度方向保持不变。

根据平面应变的定义有

2 二维应力应变状态

下图给出了平面微元的应力状态，由于泊松效应的存在，平面应力状态下的Z方向的正应变不为零，以及平面应变状态下的Z方向的正应力不为零，但由广义胡克定律可知无论是平面应力还是平面应变状态，应力和应变的独立变量都只有3个。

平面问题应力和应变独立变量的列向量

应力应变关系

对于平面应力状态

对于平面应变状态

3 平面三角形单元的刚度矩阵和方程的推导

step 1 单元类型的选择
平面问题的三角形单元每个节点有两个方向的自由度，每个单元共有6个自由度。