目录
本文主要介绍评分卡模型的概念及背后的思想体系,模型如何创建,以及在创建模型过程中遇到的问题和思考。
前言
为什么要做评分卡模型?
《巴赛尔协议》中明确对银行的系统性风险进行定义和划分,主要分为:信用风险、市场风险、操作风险、流动性风险、国家风险、声誉风险、法律风险、合规风险、战略风险。其中信用风险指授信方拒绝或无力按时、全额支付所欠债务时,给信用方带来的损失。
银行、消费金融等各种贷款机构,为了控制信用风险,期望通过客户历史的行为信息判断客户违约的可能性,由此决定是否授信以及授信的额度,从而减少在金融交易中存在的风险。评分卡模型在这种大背景下应运而生。
评分卡分为ABC卡三类:
A卡(Application score card)申请评分卡
B卡(Behavior score card)行为评分卡
C卡(Collection score card)催收评分卡
评分机制的区别在于:
1.使用的时间不同。分别侧重贷前、贷中、贷后;
2.数据要求不同。A卡一般可做贷款0-1年的信用分析,B卡则是在申请人有了一定行为后,有了较大数据进行的分析,一般为3-5年,C卡则对数据要求更大,需加入催收后客户反应等属性数据。
3.每种评分卡的模型会不一样。在A卡中常用的有逻辑回归,AHP等,而在后面两种卡中,常使用多因素逻辑回归,精度等方面更好。
除此之外,评分卡模型还适用于其他关于信用风险行为识别,如芝麻信用分、它可以提高花呗的额度,可以消费贷,可以不缴押金直接租车等。
信用评分模型是将模型变量WOE编码方式离散化之后运用logistic回归模型进行的一种二分类变量的广义线性模型。利用信用评分模型得到的客户信用评分,可作为是否准予授信或为授信额度和利率提供参考。接下来介绍如何创建评分卡及遇到的问题。
一、数据准备
因为不同评级模型所需要的数据也是不同的,所以在开发信用评级模型之前,要先明确我们需要解决的问题。
1.1 排除一些特定的建模客户
用于建模的客户或者申请者必须是日常审批过程中接触到的,需要排除异常情况。如 欺诈,特殊客户。
1.2 明确客户属性
根据不同的数据来源,可以分为以下几类:
- 人口统计特征:客户的基本特征,如性别,年龄、居住情况、年收入等
- 征信机构数据和外部评分:如人行征信报告、芝麻分等。
- 其他数据来源。
1.3 目标变量的确立
预测模型的一个基本原理是用历史数据来预测未来,申请者评分模型需要解决的问题是未来一段时间(如12个月)客户出现违约(如至少一次90天或90天以上逾期)的概率。先将客户标签定义为二分类,不良/逾期:观察窗口内,观察窗口内,60/90/120天算逾期日期;良好:从未或截止逾期;从未或在观察期内截止逾期
其中关于不良/逾期需要界定以下两项内容:确定违约日期时长、观察窗口期设置。
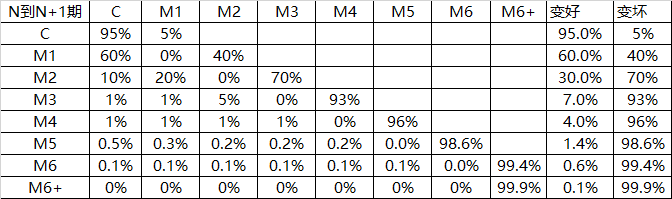
定违约日期时长,违约时长的确定可以使用逾期转移矩阵来确定,也可以按客户规则确定:
通过上图可以看出来,M3客户变坏的概率为93%.也就是说当客户逾期超过60天后,被催回的几率为7%。因此,可以定义逾期超过60天的客户为坏客户。
二、特征工程
数据准备和数据预处理阶段消耗大量的时间,主要的工作包括数据获取、探索性数据分析、缺失值处理、数据校准、数据抽样、数据转换、离散变量降维、连续变量优先分段等工作。
在评分卡模型中特别要做的是变量分箱和自变量WOE编码。
变量分箱主要指的是连续型变量化为离散型变量,为WOE编码做准备。这样做会有信息损失,但相比信息损失,过拟合带来的影响更大。
2.1 WOE和IV公式
Q1:什么是IV和WOE编码?
WOE全称是Weight of Evidence,即证据权重,也叫作自变量的一种编码。
IV全称是Information value,可通过woe加权求和得到,衡量自变量对因变量的预测能力。
要对一个变量进行WOE编码,需要首先把这个变量进行分组处理(也叫离散化、分箱等等,说的都是一个意思)。分组后,对于第i组,WOE的计算公式如下:
其中,pyi是这个组中响应客户(风险模型中,对应的是违约客户,总之,指的是模型中预测变量取值为“是”或者说1的个体)占所有样本中所有响应客户的比例,pni是这个组中未响应客户占样本中所有未响应客户的比例,#yi是这个组中响应客户的数量,#ni是这个组中未响应客户的数量,#yT是样本中所有响应客户的数量,#nT是样本中所有未响应客户的数量。
从这个公式中我们可以体会到,WOE表示的实际上是“当前分组中响应客户占所有响应客户的比例”和“当前分组中没有响应的客户占所有没有响应的客户的比例”的差异。
对这个公式做一个简单变换,可以得到:
变换以后我们可以看出,WOE也可以这么理解,他表示的是当前这个组中响应的客户和未响应客户的比值,和所有样本中这个比值的差异。这个差异是用这两个比值的比值,再取对数来表示的。WOE越大,这种差异越大,这个分组里的样本响应的可能性就越大,WOE越小,差异越小,这个分组里的样本响应的可能性就越小。
IV的计算:
有了前面的介绍,我们可以正式给出IV的计算公式。对于一个分组后的变量,第i 组的WOE前面已经介绍过,是这样计算的:
同样,对于分组i,也会有一个对应的IV值,计算公式如下:
有了一个变量各分组的IV值,我们就可以计算整个变量的IV值,方法很简单,就是把各分组的IV相加:
其中,n为变量分组个数。
2.2 WOE实例:
假设我们需要构建一个预测模型,这个模型是为了预测公司的客户集合中的每个客户对于我们的某项营销活动是否能够响应,或者说我们要预测的是客户对我们的这项营销活动响应的可能性有多大。假设我们已经从公司客户列表中随机抽取了100000个客户进行了营销活动测试,收集了这些客户的响应结果,作为我们的建模数据集,其中响应的客户有10000个。另外假设我们也已经提取到了这些客户的一些变量,作为我们模型的候选变量集,这些变量包括以下这些(实际情况中,我们拥有的变量可能比这些多得多,这里列出的变量仅仅是为了说明我们的问题):
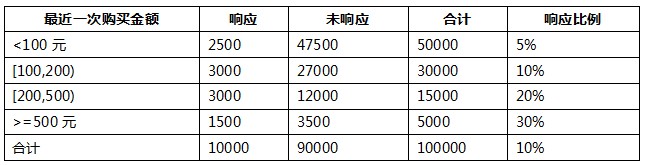
我们以其中的一个变量“最近一次购买金额”变量为例:








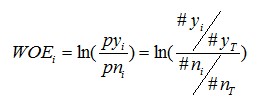
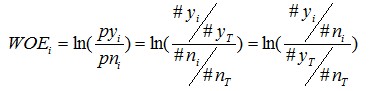
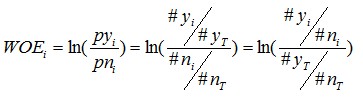
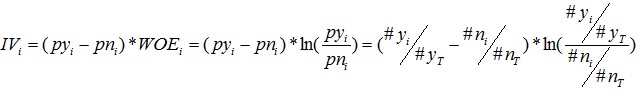
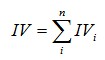
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 5531
5531











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








