看懂python3 之statsmodels包summary的参数解释

最新推荐文章于 2025-03-11 09:00:00 发布

白小跳

最新推荐文章于 2025-03-11 09:00:00 发布

阅读量1.8w

点赞数 21

分类专栏： python 数据分析 R- squared 文章标签： python3 statsmodels

本文链接：https://blog.csdn.net/weixin_44090397/article/details/97922297

版权

python 同时被 3 个专栏收录

1 篇文章

订阅专栏

数据分析

1 篇文章

订阅专栏

R- squared

1 篇文章

订阅专栏

放上代码例子：

# -*-coding:utf-8 -*-
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
import numpy as np
import time, datetime
import statsmodels.api as sm

df = pd.read_csv('D:\work\数据分析\换师次数学生状态关系\全部学员课消状态表.csv',encoding='gbk')
# data = df.ix[:, ['student_id','累计课消','学生状态']]
data=list(df['累计课消'])
data0 = df[df['学生状态'] == 0]
data1 = df[(df['学生状态'] == 1)]
data2 = df[df['学生状态'] == 2]
data3 = df[df['学生状态'] == 3]
data4 = df[df['学生状态'] == 4]

data_0 = list(data0['累计课消'])
data_1 = list(data1['累计课消'])
data_2 = list(data2['累计课消'])
data_3 = list(data3['累计课消'])
data_4 = list(data4['累计课消'])

list_bin=list(np.arange(3,255,3))

def count_y(object):
    list_count = [0 for i in range(84)]
    out_range_count=[]
    for i in list_bin:
        for k in object:
            if k < i and k >= i-3:
                bin_index=list_bin.index(i)
                list_count[bin_index] += 1
    for k in object:
        if k >= 252:
            list_count[-1] += 1
    list_array = np.array(list_count)
    return list_array

y = count_y(data)

refund=pd.Series(y_5/y)
class_fire=pd.Series(list_bin)
X = sm.add_constant(class_fire)
est=sm.OLS(refund,X).fit()
est.summary()

输出：

在这里插入图片描述

参数解释

左边：（模型背景描述）
Dep.Variable: 输出变量的名称
Model :模型名称
Method: 方法其中 Least Squares 表示最小二乘法
Date：日期
Time：时间
No.Observations: 样本数目
Df Residuals : 残差自由度 (观测数No.Observations - (参数数目Df Model+1常数))
–残差代表的是实际观察值与估计值的差
Df Model: 模型参数个数，相当于输入的X的元素个数

右边：（模型质量描述）（需要参考判断的数据）
R- squared : 可决系数，用来判断估计的准确性，范围在 [0,1] 约接近1 ，说明对y的解释能力越强，拟合越好

在这里插入图片描述
）
Adj-R- squared: 通过样本数量与模型数量对R-squared进行修正，奥卡姆剃刀原理，避免描述冗杂

(
在这里插入图片描述
）

F-statistic : 衡量拟合的显著性, 重要程度。模型的均方误差除以残差的均方误差,值越大,H0 越不可能

Prob(F-statistic): 当prob（F-statistic）<α时，表示拒绝原假设，即认为模型是显著的；
当prob（F-statistic）>α时，表示接受原假设，即认为模型不是显著的

Log likelihood （对数似然比LLR） :(很多说法是值越大，说明模型拟合的较好)(但有待考察,似然比服从统计量,大于卡方临界值拒绝原假设), 似然:
在这里插入图片描述
相当于概率:

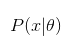
通过最大似然估计参数的选取的拟合性
（Davidson 与MacKinnon(1993)年说：对于线性回归模型，不管它误差是不是正态分布，都不需要过问LM，W，LLR，因为这些信息已被F检验所含有）

AIC: AIC可以表示为： AIC=2k-2ln(L) 其中：k是参数的数量，L是似然函数。衡量拟合优良性,选择AIC 最小的模型, 引入了惩罚项,避免参数过多,过拟合
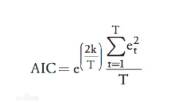
在这里插入图片描述
BIC: 贝叶斯信息准则 BIC=kln(n)-2ln(L) ,BIC相比AIC在大数据量时对模型参数惩罚得更多，导致BIC更倾向于选择参数少的简单模型。

下半部分:(模型描述)
coef: 系数 const表示常数项
std err :系数估计的基本标准误差
t : t 统计值,衡量系数统计显著程度的指标
P>|t| : 系数= 0的零假设为真的P值。如果它小于置信水平，通常为0.05，则表明该术语与响应之间存在统计上显着的关系。度的指标
[0.025,0.975]: 95％置信区间的下限和上限值

Omnibus :属于一种统计测验,测试一组数据中已解释方差是否显著大于未解释方差,但omnibus不显著,模型也可能存在合法的显著影响, 比如两个变量中有一个不显著,即便另一个显著.通常用于对比
Prob(Omnibus):将上面的统计数据变成概率

Durbin-Watson : 残差是否符合正态分布,在2左右说明是服从正态分布的,偏离2太远,解释能力受影响
是否自相关, 受到前后影响 ,与表中上限进行比较,如果D>上限不存在相关性 .
D<下限存在正相关性,在上下限之间,无法得出结论
Skewness: 偏度, 关于平均值的数据对称性的度量。正态分布误差应是关于平均值对称的分布。
Kurtosis: 峰度, 分布形状的量度,比较接近均值与远离均值的数据量如果大于三,说明峰的形状比较陡峭,形状较尖
正态分布的峰度（系数）为常数3，均匀分布的峰度（系数）为常数1.8
Jarque-Bera(JB) : Jarque–Bera检验是对样本数据是否具有符合正态分布的偏度和峰度的拟合优度的检验。
其统计测试结果总是非负的。如果结果远大于零，则表示数据不具有正态分布。

Prob(JB): 上面统计量的概率形式

Cond. No :多重共线性测试(如果多个参数,这些参数是否相互关联)