常见激活函数（Sigmoid、Tanh、Relu、Leaky Relu、Softmax）

目录

一、激活函数的作用

二、常见激活函数分析

1. Sigmoid

2. Tanh

3. Relu

4. Leaky Relu

5. Softmax

---

一、激活函数的作用

激活函数是人工神经网络中一个关键的组成部分，它被设计用来引入非线性特性到神经网络模型中。
在神经网络的基本结构中，每个神经元接收输入信号，对其进行加权求和后加上偏置项，然后将这个结果通过激活函数进行转换，得到神经元的输出。
如果没有激活函数，无论神经网络有多少层，其输出都将仅仅是一个线性组合，这样的模型表达能力非常有限，无法解决复杂的非线性问题。

激活函数的作用可以总结为以下几点：

1. 引入非线性：这是激活函数最重要的作用。由于大多数实际问题都是非线性的，非线性激活函数使得神经网络能够拟合复杂的函数映射关系，从而解决非线性问题。

2. 控制神经元输出范围：不同的激活函数有不同的输出范围，比如Sigmoid函数的输出在(0, 1)之间，Tanh函数的输出在(-1, 1)之间，ReLU函数的输出在[0, ∞)之间。这些特性有助于控制神经元的输出，防止数值不稳定。

3. 加速训练：某些激活函数（如ReLU）具有计算效率高的优点，因为它们的计算只涉及到基本的算术操作，而不需要昂贵的指数运算。

4. 缓解梯度消失/爆炸问题：一些激活函数（如ReLU及其变种）被设计来避免梯度消失或梯度爆炸问题，这些问题在训练深度神经网络时尤为突出。

二、常见激活函数分析

1. Sigmoid

数学表达式为：

函数图像为：

导数为：

导数图像为：

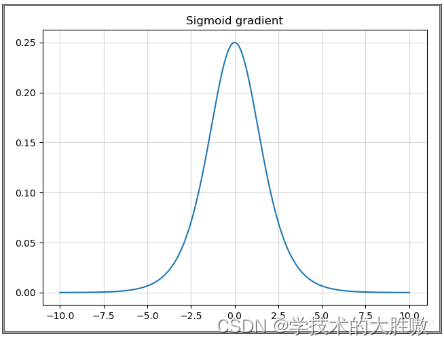
在导数中当输入值为0时，sigmoid函数的导数达到最大值0.25；而输入在任一方向上越远离0点时，导数越接近0。

sigmoid优点

• 输出范围明确：Sigmoid函数的输出范围在0到1之间，非常适合作为模型的输出函数。用于输出一个0到1范围内的概率值，比如用于表示二分类的类别或者用于表示置信度。
• 便于求导：梯度平滑，便于求导，防止模型训练过程中出现突变的梯度。

sigmoid缺点

• 梯度消失：导函数图像中，sigmoid的导数都是小于0.25的，那么在进行反向传播的时候，梯度相乘结果会慢慢的趋向于0。这样几乎就没有梯度信号通过神经元传递到前面层的梯度更新中，因此这时前面层的权值几乎没有更新。
• 非零中心化输出：Sigmoid函数的输出不是以0为中心的，而是以0.5为中心。这意味着在训练过程中，输出值总是偏向正值，可能导致权重更新偏向于一个方向，会呈Z型梯度下降，影响学习效率。
• 饱和性：Sigmoid函数的饱和性导致其在输入值的极端情况下对输入变化不敏感，这限制了网络对极端值的学习能力。
• 计算资源消耗：Sigmoid函数涉及指数运算，这在计算上可能比其他一些激活函数（如ReLU）更加耗时。

2. Tanh

数学表达式为：

实际上，Tanh函数是 sigmoid 的变形：

函数图像为：

当输入在0附近时，tanh函数接近线形变换。函数的形状类似于sigmoid函数，tanh是“零为中心”的。因此在实际应用中，tanh会比sigmoid更好一些。

导数为：

导数图像为：

当输入接近0时，tanh函数的导数接近最大值1。与sigmoid函数图像中看到的类似，输入在任一方向上远离0点，导数越接近0。

Tanh优点：

• 与sigmoid相比，多了一个零中心化输出。这有助于数据的稳定性和收敛性，因为它可以减少学习过程中的偏移。

Tanh缺点：

• 梯度消失问题：尽管Tanh函数在输入接近0时的梯度较大，但在输入值非常大或非常小的情况下，Tanh函数的导数仍然会接近0，导致梯度消失问题。
• 计算资源消耗：Tanh函数涉及指数运算，这可能比其他一些激活函数（如ReLU）在计算上更加耗时。
• 初始化敏感性：Tanh函数对权重初始化较为敏感，如果权重初始化不当，可能会导致梯度消失或爆炸问题。

3. Relu

ReLU提供了一种非常简单的非线性变换。给定元素x，ReLU函数被定义为该元素与0的最大值。

函数及图像：

导数及其图像：

ReLU优点：

• ReLU解决了梯度消失的问题，当输入值为正时，神经元不会饱和
• 计算复杂度低，不需要进行指数运算

ReLU缺点：

• 与Sigmoid一样，其输出不是以0为中心的
• Dead ReLU 问题。当输入为负时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新

4. Leaky Relu

函数：

图像：

Leaky ReLU优点：

• 解决了ReLU输入值为负时神经元出现的死亡的问题
• 计算复杂度低，不需要进行指数运算

Leaky ReLU缺点：

• 函数中的α，需要通过先验知识人工赋值（一般设为0.01）
• 有些近似线性，导致在复杂分类中效果不好。

5. Softmax

Softmax 可以使正样本（正数）的结果趋近于 1，使负样本（负数）的结果趋近于 0；且样本的绝对值越大，两极化越明显。

Softmax 可以使数值较大的值获得更大的概率。

表达式为：

导数为：

Softmax优点：

• 概率解释：Softmax函数的输出值总和为1，可以被解释为概率分布，这使得它非常适合用于多分类问题。每个类别的输出值表示该类别的相对概率。
• 梯度稳定性：由于Softmax函数的输出是归一化的，它倾向于产生更稳定的梯度，这有助于在反向传播过程中的权重更新。
• 避免梯度消失：Softmax函数不会像Sigmoid或Tanh函数那样在输入值非常大或非常小的情况下产生梯度消失问题，因为它的梯度不会接近零。

Softmax缺点：

• 数值稳定性问题：当输入特征值非常大或非常小时，Softmax函数可能会导致数值稳定性问题，因为指数函数的值可能变得非常大，导致数值溢出。
• 计算资源消耗：Softmax函数涉及指数运算和求和，这可能比其他一些激活函数（如ReLU）在计算上更加耗时。
• 对标签错误敏感：在训练过程中，如果标签错误，Softmax函数可能会放大这种错误，因为它会将概率集中在错误的类别上。
• 不适合不平衡数据：在类别不平衡的数据集中，Softmax函数可能会偏向于多数类，因为它倾向于将概率集中在概率最高的类别上。
• 输出不是零中心化：与Tanh函数不同，Softmax函数的输出不是零中心化的，这可能会影响某些类型的网络训练。
• 对输入特征敏感：Softmax函数对输入特征的缩放和范围非常敏感，如果输入特征没有适当地归一化或标准化，可能会导致训练过程中的问题。
• 不适合非分类任务：Softmax函数主要用于分类任务，如果用于回归或其他非分类任务，可能不是最佳选择。