通过遍历序列构造二叉树（扩展二叉树的先序、先序和中序、后序和中序、层序和中序）附可执行完整代码

最新推荐文章于 2025-03-17 22:54:54 发布
最新推荐文章于 2025-03-17 22:54:54 发布
阅读量6.1k 收藏 64
点赞数 13
分类专栏： 经典编程题——二叉树与树 文章标签： 二叉树 算法 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_44162361/article/details/117281549
版权
本文详细介绍了如何利用先序遍历、中序遍历、后序遍历和层序遍历序列构建二叉树，包括扩展二叉树、基于不同遍历序列的构造算法及其代码示例。通过实例展示了如何根据给定的遍历序列创建完整的二叉树结构并验证其正确性。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

文章目录

二叉树的构造

 可以构建一棵二叉树的几个方法：

  • 扩展二叉树的先序遍历序列
  • 前序遍历序列和中序遍历序列
  • 后序遍历序列和中序遍历序列
  • 层序遍历序列和中序遍历序列

 注意，只有前序遍历序列和后序遍历序列是不能唯一的确定一棵二叉树的。

扩展二叉树的先序遍历序列构造二叉树

题目描述：
 在二叉树的所有空指针位置加入虚拟结点，就构成扩展二叉树。二叉树原有的结点称为内结点，新增的虚拟节点称为外结点。
 设已知扩展二叉树的先序遍历序列，并用在原二叉树中不可能出现的值作为虚拟结点的值，如 “#” 表示外结点的值。
 设计一个算法，使用这样一个先序遍历序列，建立树的二叉链表。

算法思想：
 每读入一个值，若该值为"#"，则返回空，继续读入下一个值；如果该值不为"#"，那么就为它建立结点，结点值为该值，然后将该结点作为根结点，其地址通过函数的引用型参数root直接链接到作为实际参数的指针中。然后分别对左、右子树递归的建立子树。

实现代码：

//扩展二叉树的先序遍历序列
void BuildTree_Pre(BNode * & root, char pre[], int & i){
    if(pre[i] == '#'){ //外结点，即空结点
        i++;
        root = NULL;
    }else{
        root = (BNode *)malloc(sizeof(BNode)); //建立根结点
        root->data = pre[i];
        i++;
        BuildTree_Pre(root->lchild, pre, i); //递归建立左子树
        BuildTree_Pre(root->rchild, pre, i); //递归建立右子树
    }
}

另外，还有一种写法请参照二叉树遍历应用之根据前序遍历建树
思路是一致的，如果不理解引用型参数的可以参照这篇文章中的写法。

实例：
在这里插入图片描述

 如上图所示，所有结点值为"#"的结点位于原二叉树的空子树结点的位置，按照先序遍历所得到的先序遍历序列为ABC##DE#G##F###。
 若要建立如上所示的二叉树，则输入就应为ABC##DE#G##F###。


 这里给出可执行的完整代码，为了验证构造的二叉树，构造完二叉树后，再输出其层序遍历的结果。

#include<bits/stdc++.h>
using namespace std;

typedef struct BNode{
    char data;
    struct BNode *lchild;
    struct BNode *rchild;
}BNode;

//扩展二叉树的先序遍历序列
void BuildTree_Pre(BNode * & root, char pre[], int & i){
    if(pre[i] == '#'){ //外结点，即空结点
        i++;
        root = NULL;
    }else{
        root = (BNode *)malloc(sizeof(BNode)); //建立根结点
        root->data = pre[i];
        i++;
        BuildTree_Pre(root->lchild, pre, i); //递归建立左子树
        BuildTree_Pre(root->rchild, pre, i); //递归建立右子树
    }
}

//层序遍历
void levelOrder(BNode *root){
    queue<BNode *> treenode;
    if(root != NULL)
        treenode.push(root);
    while(!treenode.empty()){
        BNode *p = treenode.front();
        treenode.pop();
        printf("%c ",p->data);
        if(p->lchild != NULL)
            treenode.push(p->lchild);
        if(p->rchild != NULL)
            treenode.push(p->rchild);
    }
}


int main(){
    char pre[100];
    BNode *root;;
    scanf("%s",pre);
    int i = 0;
    BuildTree_Pre(root, pre, i); 
    levelOrder(root);
    return 0;
}

 执行结果：
在这里插入图片描述


先序遍历序列和中序遍历序列构造二叉树

题目描述：
 给定一棵二叉树的先序遍历序列pre[s1…t1]和中序遍历序列in[s2…t2]，设二叉树采用二叉链表存储，设计一个算法构造这棵二叉树。

算法思想：
 算法的实现步骤如下：
 1）根据先序遍历序列确定树的根结点；
 2）根据根结点在中序序列中的次序划分出二叉树的左子树、右子树包含哪些结点，
 然后根据左、右子树结点在先序序列中的次序确定子树的根结点，即回到步骤1）。
 重复上述步骤，直到每棵子树仅有一个结点（该子树的根结点）为止。
如下图所示：
 若前序遍历序列为：ABCDEFGHI
 中序遍历序列为：BCAEDGHFI
在这里插入图片描述

实现代码：

//先序遍历和中序遍历建树
BNode *PreInCreate(char pre[], char in[], int s1, int t1, int s2, int t2){
    //s1,t1为先序遍历序列的第一个结点和最后一个结点的下标
    //s2,t2为中序遍历序列的第一个结点和最后一个结点的下标
    //初始时s1=s2=0, t1=t2=n-1
    BNode *root = (BNode *)malloc(sizeof(BNode)); //建立根结点
    root->data = pre[s1]; //根结点
    int i;
    for(i=s2; in[i]!=root->data; i++); //找根结点在中序遍历序列中的位置
    int llen = i-s2; //左子树长度
    int rlen = t2-i; //右子树长度
    if(llen != 0) //递归建立左子树
        root->lchild = PreInCreate(pre, in, s1+1, s1+llen, s2, s2+llen-1);
    else //左子树为空
        root->lchild = NULL;
    if(rlen != 0)//递归建立右子树
        root->rchild = PreInCreate(pre, in, t1-rlen+1, t1, t2-rlen+1, t2);
    else //右子树为空
        root->rchild = NULL; 
    return root;
}

 或者，也可以使用引用型参数进行实现，实现的思路是一致的。

void PreInCreate2(BNode *&root, char pre[], char in[], int s1, int t1, int s2, int t2){
    if(s1<=t1){
        root = (BNode *)malloc(sizeof(BNode));
        root->data = pre[s1];
        root->lchild = NULL;
        root->rchild = NULL;
        int i;
        for(i=0; in[i]!=root->data; i++);
        int llen = i-s2; //左子树长度
        int rlen = t2-i; //右子树长度
        PreInCreate2(root->lchild, pre, in, s1+1, s1+llen, s2, s2+llen-1); //递归建立左子树
        PreInCreate2(root->rchild, pre, in, t1-rlen+1, t1, t2-rlen+1, t2); //递归建立右子树
    }
}

 这里给出可执行的完整代码，为了验证构造的二叉树，构造完二叉树后，再输出其层序遍历的结果。

#include<bits/stdc++.h>
using namespace std;

typedef struct BNode{
    char data;
    struct BNode *lchild;
    struct BNode *rchild;
}BNode;

//层序遍历
void levelOrder(BNode *root){
    queue<BNode *> treenode;
    if(root != NULL)
        treenode.push(root);
    while(!treenode.empty()){
        BNode *p = treenode.front();
        treenode.pop();
        printf("%c ",p->data);
        if(p->lchild != NULL)
            treenode.push(p->lchild);
        if(p->rchild != NULL)
            treenode.push(p->rchild);
    }
}

//先序遍历和中序遍历建树
BNode *PreInCreate(char pre[], char in[], int s1, int t1, int s2, int t2){
    //s1,t1为先序遍历序列的第一个结点和最后一个结点的下标
    //s2,t2为中序遍历序列的第一个结点和最后一个结点的下标
    //初始时s1=s2=0, t1=t2=n-1
    BNode *root = (BNode *)malloc(sizeof(BNode)); //建立根结点
    root->data = pre[s1]; //根结点
    int i;
    for(i=s2; in[i]!=root->data; i++); //找根结点在中序遍历序列中的位置
    int llen = i-s2; //左子树长度
    int rlen = t2-i; //右子树长度
    if(llen != 0) //递归建立左子树
        root->lchild = PreInCreate(pre, in, s1+1, s1+llen, s2, s2+llen-1);
    else //左子树为空
        root->lchild = NULL;
    if(rlen != 0)//递归建立右子树
        root->rchild = PreInCreate(pre, in, t1-rlen+1, t1, t2-rlen+1, t2);
    else //右子树为空
        root->rchild = NULL; 
    return root;
}

void PreInCreate2(BNode *&root, char pre[], char in[], int s1, int t1, int s2, int t2){
	//s1,t1为先序遍历序列的第一个结点和最后一个结点的下标
    //s2,t2为中序遍历序列的第一个结点和最后一个结点的下标
    //初始时s1=s2=0, t1=t2=n-1
    if(s1<=t1){
        root = (BNode *)malloc(sizeof(BNode));
        root->data = pre[s1];
        root->lchild = NULL;
        root->rchild = NULL;
        int i;
        for(i=0; in[i]!=root->data; i++);
        int llen = i-s2; //左子树长度
        int rlen = t2-i; //右子树长度
        PreInCreate2(root->lchild, pre, in, s1+1, s1+llen, s2, s2+llen-1); //递归建立左子树
        PreInCreate2(root->rchild, pre, in, t1-rlen+1, t1, t2-rlen+1, t2); //递归建立右子树
    }
}


int main(){
    char pre[100];
    char in[100];
    BNode *root;
    BNode *root2;
    int s1=0,s2=0;
    int t1,t2;
    scanf("%s",pre);
    scanf("%s",in);
    t1 = strlen(pre)-1;
    t2 = strlen(in)-1;
    root = PreInCreate(pre, in, s1, t1, s2, t2);
    levelOrder(root);
    printf("\n");
    PreInCreate2(root2, pre, in, s1, t1, s2, t2);
    levelOrder(root2);
    return 0;
}

 执行结果：
在这里插入图片描述


后序遍历序列和中序遍历序列构造二叉树

题目描述：
 给定一棵二叉树的后序遍历序列post[s1…t1]和中序遍历序列in[s2…t2]，设二叉树采用二叉链表存储，设计一个算法构造这棵二叉树。

算法思想：
 算法的实现步骤如下：
 1）根据后序遍历序列确定树的根结点；
 2）根据根结点在中序序列中的次序划分出二叉树的左子树、右子树包含哪些结点，
 然后根据左、右子树结点在后序序列中的次序确定子树的根结点，即回到步骤1）。
 重复上述步骤，直到每棵子树仅有一个结点（该子树的根结点）为止。
注意，这里与先序序列和中序序列构造二叉树的不同之处在于，先递归建立右子树，再递归建立左子树，这是由于
如下图所示：
 若后序遍历序列为：CBEHGIFDA
 中序遍历序列为：BCAEDGHFI
在这里插入图片描述

实现代码：

BNode *PostInCreate(char post[], char in[], int s1, int t1, int s2, int t2){
    //s1,t1为后序遍历序列的第一个结点和最后一个结点的下标
    //s2,t2为中序遍历序列的第一个结点和最后一个结点的下标
    //初始时s1=s2=0, t1=t2=n-1
    BNode *root = (BNode *)malloc(sizeof(BNode)); //建立根结点
    root->data = post[t1]; //根结点
    int i;
    for(i=s2; in[i]!=root->data; i++); //找根结点在中序遍历序列中的位置
    int llen = i-s2; //左子树长度
    int rlen = t2-i; //右子树长度
    if(llen != 0) //递归建立左子树
        root->lchild = PostInCreate(post, in, s1, s1+llen-1, s2, s2+llen-1);
    else //左子树为空
        root->lchild = NULL;
    if(rlen != 0) //递归建立右子树
        root->rchild = PostInCreate(post, in, t1-rlen, t1-1, t2-rlen+1, t2);
    else //右子树为空
        root->rchild = NULL;
    return root;
}

 或者，也可以使用引用型参数进行实现，实现的思路是一致的。

void PostInCreate2(BNode *&root, char post[], char in[], int s1, int t1, int s2, int t2){
    //s1,t1为后序遍历序列的第一个结点和最后一个结点的下标
    //s2,t2为中序遍历序列的第一个结点和最后一个结点的下标
    //初始时s1=s2=0, t1=t2=n-1
    if(s1<=t1){
        root = (BNode *)malloc(sizeof(BNode));
        root->data = post[t1];
        root->lchild = NULL;
        root->rchild = NULL;
        int i;
        for(i=0; in[i]!=root->data; i++); //找中序遍历序列中的根结点的位置
        int llen = i-s2; //左子树长度
        int rlen = t2-i; //右子树长度
        PostInCreate2(root->lchild, post, in, s1, s1+llen-1, s2, s2+llen-1); //递归建立左子树
        PostInCreate2(root->rchild, post, in, t1-rlen, t1-1, t2-rlen+1, t2); //递归建立右子树
    }
}

 这里给出可执行的完整代码，为了验证构造的二叉树，构造完二叉树后，再输出其层序遍历的结果。

#include<bits/stdc++.h>
using namespace std;

typedef struct BNode{
    char data;
    struct BNode *lchild;
    struct BNode *rchild;
}BNode;

//层序遍历
void levelOrder(BNode *root){
    queue<BNode *> treenode;
    if(root != NULL)
        treenode.push(root);
    while(!treenode.empty()){
        BNode *p = treenode.front();
        treenode.pop();
        printf("%c ",p->data);
        if(p->lchild != NULL)
            treenode.push(p->lchild);
        if(p->rchild != NULL)
            treenode.push(p->rchild);
    }
}


BNode *PostInCreate(char post[], char in[], int s1, int t1, int s2, int t2){
    //s1,t1为后序遍历序列的第一个结点和最后一个结点的下标
    //s2,t2为中序遍历序列的第一个结点和最后一个结点的下标
    //初始时s1=s2=0, t1=t2=n-1
    BNode *root = (BNode *)malloc(sizeof(BNode)); //建立根结点
    root->data = post[t1]; //根结点
    int i;
    for(i=s2; in[i]!=root->data; i++); //找根结点在中序遍历序列中的位置
    int llen = i-s2; //左子树长度
    int rlen = t2-i; //右子树长度
    if(llen != 0) //递归建立左子树
        root->lchild = PostInCreate(post, in, s1, s1+llen-1, s2, s2+llen-1);
    else //左子树为空
        root->lchild = NULL;
    if(rlen != 0) //递归建立右子树
        root->rchild = PostInCreate(post, in, t1-rlen, t1-1, t2-rlen+1, t2);
    else //右子树为空
        root->rchild = NULL;
    return root;
}

void PostInCreate2(BNode *&root, char post[], char in[], int s1, int t1, int s2, int t2){
    //s1,t1为后序遍历序列的第一个结点和最后一个结点的下标
    //s2,t2为中序遍历序列的第一个结点和最后一个结点的下标
    //初始时s1=s2=0, t1=t2=n-1
    if(s1<=t1){
        root = (BNode *)malloc(sizeof(BNode));
        root->data = post[t1];
        root->lchild = NULL;
        root->rchild = NULL;
        int i;
        for(i=0; in[i]!=root->data; i++); //找中序遍历序列中的根结点的位置
        int llen = i-s2; //左子树长度
        int rlen = t2-i; //右子树长度
        PostInCreate2(root->lchild, post, in, s1, s1+llen-1, s2, s2+llen-1); //递归建立左子树
        PostInCreate2(root->rchild, post, in, t1-rlen, t1-1, t2-rlen+1, t2); //递归建立右子树
    }
}


int main(){
    char post[100];
    char in[100];
    BNode *root;
    BNode *root2;
    int s1=0,s2=0;
    int t1,t2;
    scanf("%s",post);
    scanf("%s",in);
    t1 = strlen(post)-1;
    t2 = strlen(in)-1;
    root = PostInCreate(post, in, s1, t1, s2, t2);
    levelOrder(root);
    printf("\n");
    PostInCreate2(root2, post, in, s1, t1, s2, t2);
    levelOrder(root2);
    return 0;
}

 执行结果：
在这里插入图片描述


层序遍历序列和中序遍历序列构造二叉树

题目描述：
 给定一棵二叉树的层序遍历序列level[s1…t1]和中序遍历序列in[s2…t2]，设二叉树采用二叉链表存储，设计一个算法构造这棵二叉树。

算法思想：
 算法的实现描述如下：
 1.根据层序遍历序列第一个结点确定根结点；
 2.根据根结点在中序遍历序列中分割出左右子树的中序序列；
 3.根据分割出的左右子树的中序序列从层序序列中提取出对应的左右子树的层序序列；
 4.对左子树和右子树分别递归使用相同的方式继续分解；

如下图所示：
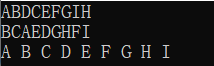
 若层序遍历序列为：ABDCEFGIH
 中序遍历序列为：BCAEDGHFI
在这里插入图片描述

实现代码：

//层序遍历序列和中序遍历序列建立二叉树
BNode *LevelInCreate(char level[], char in[], int n){
    char left[N]; //存储左子树的层序遍历
    char right[N]; //存储右子树的层序遍历
    int lcnt=0, rcnt=0;
    if(n==0)return NULL;
    //建立根结点
    BNode *root = (BNode *)malloc(sizeof(BNode));
    root->data = level[0];
    int i;
    for(i=0; in[i]!=root->data; i++); //在中序遍历中找到根结点的位置
    //划分左右子树
    for(int k=0; k<n; k++){
        //查找左子树的层序遍历
        for(int l=0; l<i; l++){
            if(in[l] == level[k])
                left[lcnt++] = level[k];
        }
        //查找右子树的层序遍历
        for(int m=i+1; m<n; m++){
            if(in[m] == level[k])
                right[rcnt++] = level[k];
        }
    }
    root->lchild = LevelInCreate(left, in, lcnt);
    root->rchild = LevelInCreate(right, in+i+1, rcnt);
    return root;
}

 这里给出可执行的完整代码，为了验证构造的二叉树，构造完二叉树后，再输出其前序遍历的结果。

#include<bits/stdc++.h>
using namespace std;

typedef struct BNode{
    char data;
    struct BNode *lchild;
    struct BNode *rchild;
}BNode;

const int N = 100;

//层序遍历序列和中序遍历序列建立二叉树
BNode *LevelInCreate(char level[], char in[], int n){
    char left[N]; //存储左子树的层序遍历
    char right[N]; //存储右子树的层序遍历
    int lcnt=0, rcnt=0;
    if(n==0)return NULL;
    //建立根结点
    BNode *root = (BNode *)malloc(sizeof(BNode));
    root->data = level[0];
    int i;
    for(i=0; in[i]!=root->data; i++); //在中序遍历中找到根结点的位置
    //划分左右子树
    for(int k=0; k<n; k++){
        //查找左子树的层序遍历
        for(int l=0; l<i; l++){
            if(in[l] == level[k])
                left[lcnt++] = level[k];
        }
        //查找右子树的层序遍历
        for(int m=i+1; m<n; m++){
            if(in[m] == level[k])
                right[rcnt++] = level[k];
        }
    }
    root->lchild = LevelInCreate(left, in, lcnt);
    root->rchild = LevelInCreate(right, in+i+1, rcnt);
    return root;
}

//前序遍历
void PreOrder(BNode *root){
    if(root!=NULL){
        printf("%c ",root->data);
        PreOrder(root->lchild);
        PreOrder(root->rchild);
    }
}


int main(){
    BNode *root;
    char level[N];
    char in[N];
    scanf("%s",level);
    scanf("%s",in);
    int n = strlen(level);
    root = LevelInCreate(level, in, n);
    PreOrder(root);
    return 0;
}

 执行结果：
在这里插入图片描述

扩展的先序遍历序列建立以二叉链表方式存储的二叉树，后序遍历
peerless1024的博客
03-29 1万+
#include<stdio.h> #include<stdlib.h>#define FALSE 0 #define TRUE 1 #define ERROR 0 #define OK 1 #define OVERFLOW -2 #define STACK_INIT_SIZE 100 #define STACKINCREMENT 10 typedef int status;//二叉树的二叉链表存
数据结构——二叉树先序、中序、后序及层次四种遍历（C语言版）
热门推荐
正弦定理的博客
12-09 36万+
数据结构——二叉树先序、中序、后序三种遍历二叉树先序、中序、后序三种遍历三、代码展示： 二叉树先序、中序、后序三种遍历 先序遍历：3 2 2 3 8 6 5 4 中序遍历：2 2 3 3 4 5 6 8 后序遍历: 2 3 2 4 5 6 8 3 三种遍历不同之处在，输出数据放在不同之处 三、代码展示： #include<stdio.h> #include<stdlib.h> typedef struct Tree{ int
重构二叉树
PZHU_CG_CSDN的博客
01-05 317
一、已知二叉树的先序序列和中序序列重建二叉树 示意图：根据示意图可以得到如下代码： node* create(int preL,int preR,int inL,int inR){ if(preL > preR){ return NULL;//先序序列的长度小于等于0时,直接返回 } node* root = new no
二叉树的层序遍历(图解+代码实现)
最新发布
云泽野の编程日记
03-17 378
在二叉树的中，二叉树的遍历中有前序遍历、中序遍历、后序遍历和层序遍历。其中前序遍历、中序遍历和后序遍历都属于深度优先搜索（DFS），而层序遍历属于广度优先遍历（BFS）。接下来为大家如何对二叉树进行层序遍历。
【教程】已知二叉树的先序序列和中序序列构造二叉树
muyuxifeng的博客
04-29 1万+
原理： 二叉树的先序序列遍历过程是：根→左→右。中序序列遍历过程是：左→根→右。 已知先序序列可以唯一确定根结点。确定完根结点之后，根据中序序列可以确定左子树和右子树。 例题： 已知某二叉树的先序序列为ABDGCEF，中序序列为DGBAECF，则构造该二叉树的过程如下图。 详细过程如下： step1：先序序列为ABDGCEF，中序序列为DGBAECF             可以.
由遍历序列构造二叉树
xiezhi123456的博客
01-24 5466
/** *    实验题目: *        由遍历序列构造二叉树 *    实验目的: *        领会二叉树的构造过程以及构造二叉树的算法设计 *    实验内容: *        设计程序，实现由先序序列和中序序列以及由中序序列和后序序列构造 *    一颗二叉树的功能(二叉树中每个结点值为单个字符)。要求以括号表示法和 *    凹入表示法输出该二叉树。并用先序遍历序列"A B ...
由遍历序列构造二叉树（C语言）
派拉斯兔子的博客
07-08 3037
一、不同的二叉树遍历序列 （一）、不同二叉树的中序遍历序列中序遍历：中序遍历左子树、根结点、中序遍历右子树（二）不同二叉树的前序遍历序列前序遍历：根结点、前序遍历左子树、前序遍历右子树 <hr/> <img src='https://img-blog.csdnimg.cn/20210708193617832.png'>
Python二叉树的遍历操作示例【前序遍历,中序遍历,后序遍历,层序遍历】
01-20
本文实例讲述了Python二叉树的遍历操作。分享给大家供大家参考，具体如下： # coding:utf-8 @ encoding: utf-8 @ author: lixiang @ email: lixiang_cn@foxmail.com @ python_version: 2 @ time: 2018/4/11 0:09 @...
Python实现输入二叉树的先序和中序遍历，再输出后序遍历操作示例
01-20
本文实例讲述了Python实现输入二叉树的先序和中序遍历，再输出后序遍历操作。分享给大家供大家参考，具体如下： 实现一个功能：  输入:一颗二叉树的先序和中序遍历  输出:后续遍历 思想： 先序遍历中，第一个元素...
二叉树遍历思路及代码（先序、中序、后序、层遍历）
weixin_48716357的博客
09-23 3439
1.定义：二叉树是n个结点的有限集合，该集合或者为空集，或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树构成。2.形态：二叉树有5种形态，分别是空二叉树、只有一个根结点、根和左孩子、跟和右孩子、根和左右孩子。3.分类：满二叉树、完全二叉树、不完全二叉树 （满二叉树是特殊的完全二叉树）对当前树进行编号从上到下从左到右依次编号，如果编号中间没有断开，而且最底层是全的，就是满二叉树；如果编号中间没有断开，最底层不是满的，是完全二叉树；如果中间编号断开，一定是不完全二叉树。
二叉树-已知先序遍历和中序遍历，如何求后序遍历
weixin_39791537的博客
02-02 1925
首先，我们要先知道二叉树通常遍历的顺序： 先序--根左右 中序--左中右 后序--左右中 层序遍历--从上至下，从左到右 然后，通过上面可以总结出用本题目的求解过程： 确定树的根节点 求解树的子树 对二叉树的左、右孩子分别进行步骤1、2，直到求出二叉树结构为止。 最后，实现代码如下： package tree; public class BinaryTree { pri...
根据前序遍历序列和中序遍历序列构造二叉树
菜鸟蜗居地
08-20 1299
转载地址：http://blog.csdn.net/yunzhongguwu005/article/details/9270085 感谢作者！！！  一个前序遍历序列和一个中序遍历序列可以确定一颗唯一的二叉树。        根据前序遍历的特点, 知前序序列(PreSequence)的首个元素(PreSequence[0])为二叉树的根(root),  然后在中序序列(InSeq
扩展二叉树前序遍历序列构建二叉树（图解）
天道酬勤
04-09 4636
是 n（n >= 0）个结点（每个结点最多只有2棵子树）的有限集合，该集合可为空集（称为空二叉树），或由一个根节点和两颗互不相交的，称为根节点的左子树和右子树的二叉树组成。：将二叉树中的每个结点的空子结点用一个虚拟结点表示，其值为一特定的值，比如"#"，这样每个结点都有两个子结点，这种处理后的二叉树为原二叉树的扩展树。扩展二叉树就可以做到一个遍历序列确定一颗二叉树。例如：图1为一颗二叉树，图2为这颗二叉树的扩展二叉树：先访问根结点，然后遍历左子树，最后遍历右子树。
c语言通过前序遍历构建二叉树
安权_code的博客
11-24 6567
在链式二叉树中，我们一般都是通过一个建立好的二叉树从而算出他的前序遍历，那么如何通过一个前序遍历来创建一个二叉树呢，本文将详细解读前序遍历每一个步骤是如何创建二叉树的。
二叉树——遍历序列构造二叉树
一个很懒的人
08-22 586
0.概述 本文首先给出四种遍历算法的特点，其次给出不能构造唯一二叉树的两种情况，最后给出先序+中序、后序+中序、层次+中序、三种遍历序列构造二叉树的方法！ 1.四种遍历算法的特点 2.不能构造唯一二叉树的两种情况 （1）只给出四种遍历序列的 某一种 （2）未给出 中序 遍历序列 3.遍历序列构造二叉树 （1）先序 + 中序 （2）后序 + 中序 （3）层次+ 中序 情况1： 情况2： ...
由先序遍历与中序遍历构建一棵二叉树
二哈
06-09 7413
1. 问题描述： 已知二叉树节点按先序遍历下的序列存储在一维数组pre[l1, ....r1]中，按中序遍历下的序列存储在一维数组中in[l2, ...r2]中，其中l1，r1，l2，r2指示了数组中元素（类型为char型）存储的下标范围，假定二叉树中节点的值互不相同，试写出由pre[l1...r1]和in[l2,...r2]构造出二叉树的算法 2. 思路分析： ① 我们根据二叉树遍历的性质...
通过树的先序和中序遍历序列来构造二叉树
一路前行的专栏
05-08 2895
通过树的先序和中序遍历序列来构造二叉树
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值