Logistic回归

目录

1、引出问题

2、实例解释

3、代价函数

4、简化代价函数和梯度下降

5、多对一问题

---

---

---

1、引出问题

当我们处理二分类问题的时候，很显然线性回归算法已经不能不能很好的满足我们的需要。那么由此引入Logistic 回归（实际用于处理分类问题）。

对于二分类问题，只有只有正类和负类，通常用0/1来表示，可以引出g(z)函数是比较符合需求的。

当g(z)>=0.5时，我们预测值为1，当g(z)<0.5时，我们预测值为0；

同时也可推出当在z>=0时，g(z)>=0.5;

又z=θTx,所以θTx>=0时，我们预测值为1，当θTx<0时，我们预测值为0;

2、实例解释

我们来看一个例子。我们假设h(x)函数用来拟合这些数据，并假设事先已经知道 θo=-1,θ1=0,θ2=0,θ3=1,θ4=1(稍等将解释怎么计算出θ的大小）。

由之前的结论θTx>=0时，我们预测值为1；

在该示例中，θTx=θo+θ1x1+θ2x2+θ3x1^2θ4x2^2  代入θ的值   θTx=-1+x1^2+x2^2

-1+x1^2+x2^2>=0      可推出     x1^2+x2^2>=1

3、代价函数

那么，我们又应该如何选取代价函数呢？如果我们继续使用原先引出的代价函数，如下图所示的话，我们得到的代价函数可能就是非凸函数了（有很多局部最优点），如果用梯度下降法来计算的话，可能就无法得到想要的结果了。

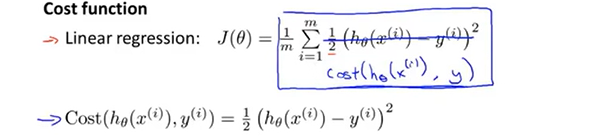
那么我们引出下图代价函数，我们来讨论预测的两种情况

当y=1时，①h(x)=1, y=1, 那么cost=0 ;

                 ②h(x)=0, y=1, 那么cost=∞ ;

当y=0时，①h(x)=1, y=0, 那么cost=∞ ;

                 ②h(x)=0, y=0, 那么cost=0 ;

 

 由上分析可知，以上代价函数是比较符合我们对二分类的需求的。

 4、简化代价函数和梯度下降

我们可以将代价函数简化为蓝色字体的函数。

在用梯度下降时，我们还需要注意的是，与之前不同的h(x)函数

5、多对一问题

当我们遇到多分类问题的时候，应该怎么处理呢？

比如，我们需要对天气进行预测，晴天、雨天、阴天；

我们采用到，当需要对“△”进行分类时，将“△”当做正类，将“□”和“×”都当做负类；

当需要对“□”进行分类时，将“□”当做正类，将“△”和“×”当做负类；

以此类推；