前言
为什么强化学习常用图结构表示
在强化学习(Reinforcement Learning, RL)中,图结构常用于表示环境、状态和动作的关系,因为图结构能够直观且有效地捕捉复杂的关系和依赖性。下面详细解释强化学习中为何常用图结构表示。
1. 强化学习中的核心元素
强化学习的核心包括:
- 状态空间(States):环境的不同状态。
- 动作空间(Actions):智能体在每个状态下可以采取的不同动作。
- 转移概率(Transition Probability):从一个状态转移到另一个状态的概率。
- 奖励(Reward):采取某一动作后智能体获得的奖励。
这些元素天然适合用图来建模:
- 节点表示状态或环境中的位置。
- 边表示状态之间的转移关系,由智能体的动作触发。
- 边的权重可以是转移概率或奖励值。
2. 图结构的直观性和清晰性
在强化学习问题中,图结构可以用来直观地展示状态与动作之间的复杂关系。例如:
- 状态转移图:状态之间的转移关系由图中的边表示,每条边代表一种动作导致的转移。
- 马尔科夫决策过程(MDP):MDP 是强化学习中的基础模型,定义了状态、动作和转移概率。这些元素构成的依赖关系非常适合用有向图表示。
3. 图结构支持复杂环境的建模
一些复杂的强化学习问题需要表示大量状态和动作,例如:
- 迷宫导航:用图结构表示不同位置(状态)之间的路径。
- 机器人控制:用图来表示机器人不同状态之间的转移。
- 多智能体强化学习:多个智能体的相互关系和协作任务也可以用图结构来描述。
4. 适用于图神经网络(GNN)
- 在强化学习中,图神经网络(Graph Neural Networks, GNN)正在兴起,它们利用图结构来表示和学习状态之间的复杂关系。
- 图神经网络能够有效处理强化学习中的稀疏表示问题和高维状态空间,帮助提升策略的学习能力。
5. 解决路径规划与最优策略问题
强化学习中的一些经典问题(如路径规划、最优策略)本质上是图搜索问题:
- 路径规划:寻找从起始状态到目标状态的最优路径。
- Q-learning:通过在状态-动作空间的图中更新 Q 值,找到最优策略。
6. 并行计算和优化
- 使用图结构可以将强化学习问题转化为图搜索算法,如动态规划、Dijkstra算法、A*算法等。这些算法能够并行计算,提升复杂环境中的学习速度。
总结
强化学习中常用图结构表示的原因有:
- 直观地展示状态与动作之间的关系。
- 适配复杂环境,如迷宫导航、机器人控制等。
- 支持GNN模型,帮助解决稀疏和高维数据问题。
- 便于路径规划和寻找最优策略。
- 兼容并行计算,提升复杂问题的求解速度。
因此,图结构在强化学习中是一个强大且灵活的工具,为设计智能体的策略学习提供了有效支持。
一、图结构的详细描述
图(Graph)是数学和计算机科学中用于描述对象集合及其相互关系的抽象模型。它由一组顶点(Vertices)和连接这些顶点的边(Edges)组成。图结构广泛应用于网络分析、路径规划、社交网络、数据挖掘等领域。
一、图的基本概念
- 顶点(Vertex):表示对象或实体,通常用集合 V V V 表示。
- 边(Edge):表示顶点之间的连接关系,通常用集合
E
E
E 表示。
- 无向边:没有方向性,连接的两个顶点关系对等。
- 有向边(弧):具有方向性,表示从一个顶点指向另一个顶点的关系。
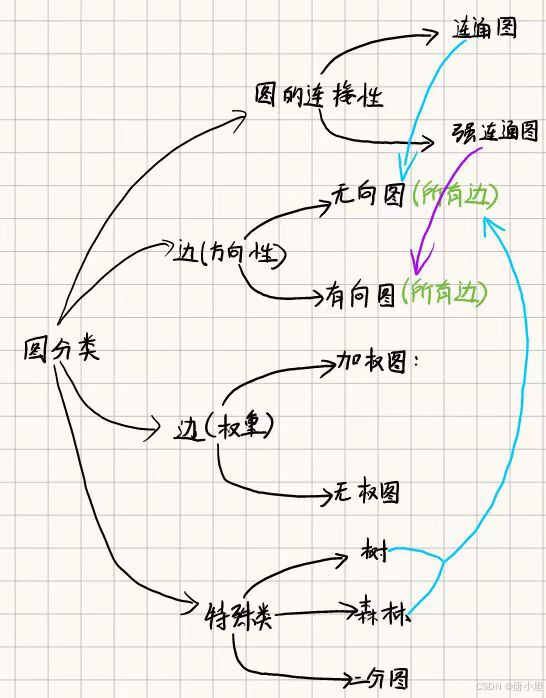
二、图的分类
-
按边的方向性
- 无向图(Undirected Graph):所有边都没有方向性。
- 有向图(Directed Graph):所有边都有明确的方向性。
-
按边的权重
- 加权图(Weighted Graph):边具有权重,表示连接代价、距离等。
- 无权图(Unweighted Graph):边没有权重,所有连接被视为等价。
-
按图的连接性
- 连通图(Connected Graph):无向图中任意两个顶点之间都有路径。
- 强连通图(Strongly Connected Graph):有向图中任意两个顶点之间都有路径相通。
-
特殊类型
- 树(Tree):一种无环连通无向图。
“无环”的意思是图中不存在任何回路(环路)**。 - 森林(Forest):由若干不相连的树组成的无向图。
- 二分图(Bipartite Graph):顶点集可分为两个不交集 ( V 1 , V 2 ) (V_1, V_2) (V1,V2),且所有边都连接这两个集合的顶点。
- 树(Tree):一种无环连通无向图。
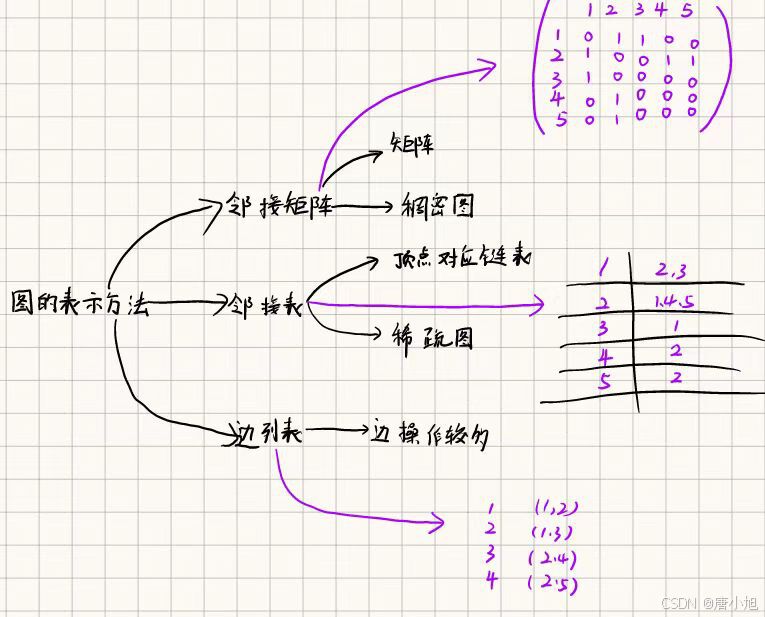
三、图的表示方法
-
邻接矩阵(Adjacency Matrix)
- 使用一个
n
×
n
n \times n
n×n 的矩阵表示,其中
n
n
n 是顶点数量。
A i j = { 1 , 如果顶点 v i 和 v j 相连 0 , 其他 A_{ij} = \begin{cases} 1, & \text{如果顶点 } v_i \text{ 和 } v_j \text{ 相连} \\ 0, & \text{其他} \end{cases} Aij={1,0,如果顶点 vi 和 vj 相连其他 - 优点:查询两个顶点是否相连速度快。
- 缺点:空间复杂度高,适合于稠密图。
- 使用一个
n
×
n
n \times n
n×n 的矩阵表示,其中
n
n
n 是顶点数量。
-
邻接表(Adjacency List)
- 每个顶点 v i v_i vi 对应一个链表,链表中存储与其相邻的顶点集合 A d j ( v i ) Adj(v_i) Adj(vi)。
- 优点:节省空间,适合于稀疏图。
- 缺点:查询特定边是否存在需要遍历链表。
-
边列表(Edge List)
- 列出所有的边 E = { ( v i , v j ) } E = \{(v_i, v_j)\} E={(vi,vj)} 及其关联的顶点。
- 适用于边的操作较多的情况。
1、邻接矩阵(Adjacency Matrix)示例:无环连通无向图的邻接矩阵表示
下面举一个无环连通无向图(树)的例子,并给出其对应的邻接矩阵。
示例图:
假设有一个包含 5 个顶点的树,顶点编号为 1、2、3、4、5,边的连接关系如下:
- 顶点 1 与 顶点 2 相连
- 顶点 1 与 顶点 3 相连
- 顶点 2 与 顶点 4 相连
- 顶点 2 与 顶点 5 相连

邻接矩阵表示:
顶点编号从 1 1 1 到 5 5 5,邻接矩阵 A A A 是一个 5 × 5 5 \times 5 5×5 的矩阵,元素 A i j A_{ij} Aij 表示顶点 i i i 和顶点 j j j 之间是否有边连接:
- A i j = 1 A_{ij} = 1 Aij=1:顶点 i i i 和顶点 j j j 之间有边
- A i j = 0 A_{ij} = 0 Aij=0:顶点 i i i 和顶点 j j j 之间没有边
邻接矩阵 A A A 如下:
A = ( 0 1 1 0 0 1 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 ) A = \begin{pmatrix} 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ \end{pmatrix} A= 0110010011100000100001000
矩阵解释:
-
第一行(顶点 1 1 1):
- A 12 = 1 A_{12} = 1 A12=1:顶点 1 1 1 与顶点 2 2 2 相连
- A 13 = 1 A_{13} = 1 A13=1:顶点 1 1 1 与顶点 3 3 3 相连
- 其余元素为 0 0 0,表示顶点 1 1 1 与其他顶点不直接相连
-
第二行(顶点 2 2 2):
- A 21 = 1 A_{21} = 1 A21=1:顶点 2 2 2 与顶点 1 1 1 相连
- A 24 = 1 A_{24} = 1 A24=1:顶点 2 2 2 与顶点 4 4 4 相连
- A 25 = 1 A_{25} = 1 A25=1:顶点 2 2 2 与顶点 5 5 5 相连
- 其余元素为 0 0 0
-
第三行(顶点 3 3 3):
- A 31 = 1 A_{31} = 1 A31=1:顶点 3 3 3 与顶点 1 1 1 相连
- 其余元素为 0 0 0
-
第四行(顶点 4 4 4):
- A 42 = 1 A_{42} = 1 A42=1:顶点 4 4 4 与顶点 2 2 2 相连
- 其余元素为 0 0 0
-
第五行(顶点 5 5 5):
- A 52 = 1 A_{52} = 1 A52=1:顶点 5 5 5 与顶点 2 2 2 相连
- 其余元素为 0 0 0
邻接矩阵的完整形式:
A = ( 1 2 3 4 5 1 0 1 1 0 0 2 1 0 0 1 1 3 1 0 0 0 0 4 0 1 0 0 0 5 0 1 0 0 0 ) A = \begin{pmatrix} & \textbf{1} & \textbf{2} & \textbf{3} & \textbf{4} & \textbf{5} \\ \textbf{1} & 0 & 1 & 1 & 0 & 0 \\ \textbf{2} & 1 & 0 & 0 & 1 & 1 \\ \textbf{3} & 1 & 0 & 0 & 0 & 0 \\ \textbf{4} & 0 & 1 & 0 & 0 & 0 \\ \textbf{5} & 0 & 1 & 0 & 0 & 0 \\ \end{pmatrix} A= 12345101100210011310000401000501000
特点说明:
- 对称性:由于是无向图,邻接矩阵是对称的,即 A i j = A j i A_{ij} = A_{ji} Aij=Aji。
- 稀疏性:矩阵中非零元素较少,适合用邻接表表示以节省空间。
- 无环性:图中不存在任何回路,从任意顶点出发都无法经过不同的边回到自身。
总结:
- 无环连通无向图(树)的邻接矩阵可以清晰地表示顶点之间的连接关系。
- 邻接矩阵适用于小规模的图,便于理解和计算。
- 通过邻接矩阵,可以方便地进行矩阵运算来分析图的性质,如计算度矩阵、拉普拉斯矩阵等。
2、邻接表示例:无环连通无向图的邻接矩阵表示
下面举一个无环连通无向图(树)的例子,并给出其对应的邻接表。
示例图:
假设有一个包含 5 个顶点的树,顶点编号为 1 1 1、 2 2 2、 3 3 3、 4 4 4、 5 5 5,边的连接关系如下:
- 顶点 1 1 1 与 顶点 2 2 2 相连
- 顶点 1 1 1 与 顶点 3 3 3 相连
- 顶点 2 2 2 与 顶点 4 4 4 相连
- 顶点 2 2 2 与 顶点 5 5 5 相连

邻接表表示:
在邻接表中,每个顶点列出与其直接相连的邻接顶点。对于顶点编号从 1 1 1 到 5 5 5 的图,其邻接表如下:
- 顶点
1
1
1:
- 邻接顶点: A d j ( 1 ) = { 2 , 3 } Adj(1) = \{2,\, 3\} Adj(1)={2,3}
- 顶点
2
2
2:
- 邻接顶点: A d j ( 2 ) = { 1 , 4 , 5 } Adj(2) = \{1,\, 4,\, 5\} Adj(2)={1,4,5}
- 顶点
3
3
3:
- 邻接顶点: A d j ( 3 ) = { 1 } Adj(3) = \{1\} Adj(3)={1}
- 顶点
4
4
4:
- 邻接顶点: A d j ( 4 ) = { 2 } Adj(4) = \{2\} Adj(4)={2}
- 顶点
5
5
5:
- 邻接顶点: A d j ( 5 ) = { 2 } Adj(5) = \{2\} Adj(5)={2}
邻接表的表格形式:
| 顶点 v v v | 邻接顶点 A d j ( v ) Adj(v) Adj(v) |
|---|---|
| 1 1 1 | 2 2 2, 3 3 3 |
| 2 2 2 | 1 1 1, 4 4 4, 5 5 5 |
| 3 3 3 | 1 1 1 |
| 4 4 4 | 2 2 2 |
| 5 5 5 | 2 2 2 |
邻接表解释:
-
顶点 1 1 1 的邻接表:
- A d j ( 1 ) = { 2 , 3 } Adj(1) = \{2,\, 3\} Adj(1)={2,3}
- 表示顶点 1 1 1 与顶点 2 2 2 和顶点 3 3 3 相连。
-
顶点 2 2 2 的邻接表:
- A d j ( 2 ) = { 1 , 4 , 5 } Adj(2) = \{1,\, 4,\, 5\} Adj(2)={1,4,5}
- 表示顶点 2 2 2 与顶点 1 1 1、 4 4 4、 5 5 5 相连。
-
顶点 3 3 3 的邻接表:
- A d j ( 3 ) = { 1 } Adj(3) = \{1\} Adj(3)={1}
- 表示顶点 3 3 3 只与顶点 1 1 1 相连。
-
顶点 4 4 4 的邻接表:
- A d j ( 4 ) = { 2 } Adj(4) = \{2\} Adj(4)={2}
- 表示顶点 4 4 4 只与顶点 2 2 2 相连。
-
顶点 5 5 5 的邻接表:
- A d j ( 5 ) = { 2 } Adj(5) = \{2\} Adj(5)={2}
- 表示顶点 5 5 5 只与顶点 2 2 2 相连。
特点说明:
- 空间效率高:邻接表只存储实际存在的边,节省空间,适合于稀疏图。
- 遍历方便:容易遍历某个顶点的所有邻接顶点,适用于深度优先搜索(DFS)和广度优先搜索(BFS)等算法。
- 无环性:由于是无环连通无向图(树),从任意顶点出发,不会存在回到起点的非重复路径。
总结:
- 邻接表是一种高效的图表示方法,特别适用于边数较少的稀疏图。
- 在邻接表中,每个顶点的邻接顶点列表可以使用链表、数组或其他数据结构实现。
- 邻接表便于实现图的遍历和搜索算法,节省空间,提高算法效率。
3、列表(Edge List)示例:无环连通无向图的边列表表示
下面举一个无环连通无向图(树)的例子,并给出其对应的边列表。
示例图:
假设有一个包含 5 个顶点的树,顶点编号为 1 1 1、 2 2 2、 3 3 3、 4 4 4、 5 5 5,边的连接关系如下:
- 顶点 1 1 1 与 顶点 2 2 2 相连
- 顶点 1 1 1 与 顶点 3 3 3 相连
- 顶点 2 2 2 与 顶点 4 4 4 相连
- 顶点 2 2 2 与 顶点 5 5 5 相连

边列表表示:
在边列表中,图的所有边被列举出来,每条边由其两个关联顶点表示。对于这个图,其边列表如下:
- 边 1 1 1: ( 1 , 2 ) (1,\, 2) (1,2)
- 边 2 2 2: ( 1 , 3 ) (1,\, 3) (1,3)
- 边 3 3 3: ( 2 , 4 ) (2,\, 4) (2,4)
- 边 4 4 4: ( 2 , 5 ) (2,\, 5) (2,5)
边列表的表格形式:
| 边编号 | 关联顶点 |
|---|---|
| 1 1 1 | ( 1 , 2 ) (1,\, 2) (1,2) |
| 2 2 2 | ( 1 , 3 ) (1,\, 3) (1,3) |
| 3 3 3 | ( 2 , 4 ) (2,\, 4) (2,4) |
| 4 4 4 | ( 2 , 5 ) (2,\, 5) (2,5) |
边列表解释:
-
边 1 1 1: ( 1 , 2 ) (1,\, 2) (1,2)
- 表示顶点 1 1 1 与顶点 2 2 2 之间有一条边。
-
边 2 2 2: ( 1 , 3 ) (1,\, 3) (1,3)
- 表示顶点 1 1 1 与顶点 3 3 3 之间有一条边。
-
边 3 3 3: ( 2 , 4 ) (2,\, 4) (2,4)
- 表示顶点 2 2 2 与顶点 4 4 4 之间有一条边。
-
边 4 4 4: ( 2 , 5 ) (2,\, 5) (2,5)
- 表示顶点 2 2 2 与顶点 5 5 5 之间有一条边。
特点说明:
- 简单直观:边列表直接列出了所有的边及其关联的顶点,形式简单。
- 空间效率:对于边数较少的稀疏图,边列表节省空间。
- 适用于边操作:方便遍历和处理边,例如计算最小生成树、最短路径等算法中,边列表常被使用。
总结:
- 边列表是一种列举图中所有边的表示方法,特别适用于边操作频繁的算法。
- 边列表适合存储边的属性,例如权重,在加权图中非常有用。
- 通过边列表,可以方便地进行排序、筛选等操作,辅助实现各种图算法。
四、图的性质

-
度(Degree)
- 无向图:顶点的度是连接到该顶点的边的数量,用 deg ( v ) \deg(v) deg(v) 表示。
- 有向图:
- 入度(In-degree):指向该顶点的边的数量, deg − ( v ) \deg^{-}(v) deg−(v)。
- 出度(Out-degree):该顶点指向其他顶点的边的数量, deg + ( v ) \deg^{+}(v) deg+(v)。
-
路径和回路
- 路径(Path):顶点的序列
P
=
⟨
v
1
,
v
2
,
…
,
v
k
⟩
P = \langle v_1, v_2, \dots, v_k \rangle
P=⟨v1,v2,…,vk⟩,其中相邻顶点由边连接,即
(
v
i
,
v
i
+
1
)
∈
E
(v_i, v_{i+1}) \in E
(vi,vi+1)∈E。
- 简单路径:不包含重复顶点的路径。
- 回路(Cycle):起点和终点相同的路径,即 v 1 = v k v_1 = v_k v1=vk。
- 路径(Path):顶点的序列
P
=
⟨
v
1
,
v
2
,
…
,
v
k
⟩
P = \langle v_1, v_2, \dots, v_k \rangle
P=⟨v1,v2,…,vk⟩,其中相邻顶点由边连接,即
(
v
i
,
v
i
+
1
)
∈
E
(v_i, v_{i+1}) \in E
(vi,vi+1)∈E。
-
连通性
- 连通分量(Connected Component):无向图的极大连通子图。
- 强连通分量(Strongly Connected Component):有向图中任意两个顶点 v v v 和 u u u,都有路径 v → u v \rightarrow u v→u 和 u → v u \rightarrow v u→v。
五、图的算法
-
遍历算法
-
深度优先搜索(DFS)
- 算法思想:沿着一个方向尽可能深入搜索,使用栈或递归实现。
- 时间复杂度: O ( ∣ V ∣ + ∣ E ∣ ) O(|V| + |E|) O(∣V∣+∣E∣)。
-
广度优先搜索(BFS)
- 算法思想:以层次的方式逐层搜索,使用队列实现。
- 时间复杂度: O ( ∣ V ∣ + ∣ E ∣ ) O(|V| + |E|) O(∣V∣+∣E∣)。
-
-
最短路径算法
-
Dijkstra 算法
- 用于计算从单个源点到其他顶点的最短路径,适用于非负权重图。
- 时间复杂度:使用二叉堆为 O ( ( ∣ V ∣ + ∣ E ∣ ) log ∣ V ∣ ) O((|V| + |E|) \log |V|) O((∣V∣+∣E∣)log∣V∣)。
-
Bellman-Ford 算法
- 可处理带有负权边的图,检测负权回路。
- 时间复杂度: O ( ∣ V ∣ ⋅ ∣ E ∣ ) O(|V| \cdot |E|) O(∣V∣⋅∣E∣)。
-
Floyd-Warshall 算法
- 计算所有顶点对之间的最短路径。
- 时间复杂度: O ( ∣ V ∣ 3 ) O(|V|^3) O(∣V∣3)。
-
-
最小生成树算法
-
Prim 算法
- 从一个顶点开始,逐步扩展生成树。
- 时间复杂度:使用最小堆为 O ( ∣ E ∣ log ∣ V ∣ ) O(|E| \log |V|) O(∣E∣log∣V∣)。
-
Kruskal 算法
- 按照边的权重从小到大选取,避免形成回路(使用并查集检测)。
- 时间复杂度: O ( ∣ E ∣ log ∣ E ∣ ) O(|E| \log |E|) O(∣E∣log∣E∣)。
-
-
拓扑排序
- 适用于有向无环图(DAG),用于确定事件的线性次序。
- 算法步骤:
- 选择一个入度为零的顶点 v v v,输出它。
- 从图中删除 v v v 及其出边,更新入度。
- 重复以上步骤,直到所有顶点被输出或无法继续(图中存在环)。
六、图的应用
-
网络通信
- 路由协议设计、网络流量优化。
- 使用最短路径算法,如 OSPF 协议中的 Dijkstra 算法。
-
社交网络分析
- 关系挖掘、影响力分析、社区发现。
- 使用连通分量、中心性指标等方法。
-
人工智能
- 状态空间搜索、约束满足问题。
- 使用图搜索算法,如 A ∗ A^* A∗ 算法。
-
生物信息学
- 基因序列比对、蛋白质相互作用网络。
- 使用图匹配、网络分析方法。
-
交通规划
- 导航系统、最优路径选择。
- 使用最短路径和最大流等算法。
七、结论
图结构是描述复杂关系和系统的强大工具。通过对图的研究和算法的应用,我们能够有效地解决实际问题,如优化资源配置、发现数据中的隐藏模式和改进系统的效率。理解图的基本概念和性质,对于从事计算机科学、数据分析和相关领域的人来说至关重要。
二、实践_代码
带权有向图的实现
如果需要表示有向边的权重,可以将邻接表中的列表从简单的顶点列表改为包含元组(邻接顶点,权重)的列表。
class WeightedDirectedGraph:
def __init__(self):
"""初始化一个带权重的有向图"""
self.adj_list = {}
def add_vertex(self, vertex):
"""添加一个顶点到图中"""
if vertex not in self.adj_list:
self.adj_list[vertex] = []
def add_edge(self, from_vertex, to_vertex, weight=1):
"""
添加一条从 from_vertex 到 to_vertex 的有向边,并指定权重。
默认权重为1。
"""
if from_vertex not in self.adj_list:
self.add_vertex(from_vertex)
if to_vertex not in self.adj_list:
self.add_vertex(to_vertex)
self.adj_list[from_vertex].append((to_vertex, weight))
def remove_edge(self, from_vertex, to_vertex):
"""移除从 from_vertex 到 to_vertex 的有向边"""
if from_vertex in self.adj_list:
self.adj_list[from_vertex] = [edge for edge in self.adj_list[from_vertex] if edge[0] != to_vertex]
def remove_vertex(self, vertex):
"""移除图中的顶点及所有相关的边"""
if vertex in self.adj_list:
del self.adj_list[vertex]
for v in self.adj_list:
self.adj_list[v] = [edge for edge in self.adj_list[v] if edge[0] != vertex]
def get_vertices(self):
"""返回图中的所有顶点"""
return list(self.adj_list.keys())
def get_edges(self):
"""返回图中的所有有向边及其权重"""
edges = []
for from_vertex, neighbors in self.adj_list.items():
for to_vertex, weight in neighbors:
edges.append((from_vertex, to_vertex, weight))
return edges
def display(self):
"""打印图的邻接表表示"""
for vertex in self.adj_list:
edges = ', '.join([f"{to}({weight})" for to, weight in self.adj_list[vertex]])
print(f"{vertex}: {edges}")
# 创建一个带权重的有向图实例
weighted_graph = WeightedDirectedGraph()
# 添加有向边及其权重
weighted_graph.add_edge('A', 'B', 5)
weighted_graph.add_edge('A', 'D', 3)
weighted_graph.add_edge('B', 'C', 2)
weighted_graph.add_edge('E', 'B', 4)
weighted_graph.add_edge('E', 'D', 1)
# 显示带权重的图的邻接表
weighted_graph.display()

问题解决: CVRP问题的加权有向图结构表述
CVRP(Capacitated Vehicle Routing Problem,容量约束车辆路径问题)可以使用加权有向图来表示。下面是该表述的详细步骤:
1. 图的构建:
- 节点(Vertices):图的节点表示客户和配送中心。设定节点集 V = { v 0 , v 1 , . . . , v n } V = \{v_0, v_1, ..., v_n\} V={v0,v1,...,vn},其中 v 0 v_0 v0 代表配送中心,其他节点 v 1 , v 2 , . . . , v n v_1, v_2, ..., v_n v1,v2,...,vn 代表客户。
- 边(Edges):边集 E E E 表示车辆在不同客户之间或客户与配送中心之间的行驶路线。每一条边 ( v i , v j ) ∈ E (v_i, v_j) \in E (vi,vj)∈E 代表从节点 v i v_i vi 到节点 v j v_j vj 的行驶路径。
2. 边的权重(Weights on edges):
- 每条边 ( v i , v j ) (v_i, v_j) (vi,vj) 上附带一个权重 w ( i , j ) w(i, j) w(i,j),表示从客户 i i i 到客户 j j j 的行驶距离或成本。这个权重通常可以是距离、时间或燃料消耗等因素的组合。
- 这些权重是定义车辆路径的优化目标的核心,比如总行驶距离最小化。
3. 车辆的容量限制:
- 每辆车
k
k
k 具有一个固定的容量
C
C
C,用于满足客户的需求。每个客户节点
v
i
v_i
vi 也有一个需求
d
i
d_i
di,表示该客户需要配送的货物量。通常要求车辆服务的客户需求总量不能超过车辆的容量,即对某一辆车
k
k
k,在经过的所有客户
S
k
S_k
Sk 中,满足约束:
∑ v i ∈ S k d i ≤ C \sum_{v_i \in S_k} d_i \leq C vi∈Sk∑di≤C
4. 目标函数(Objective function):
- CVRP的目标通常是找到最优的路径,使得所有客户的需求都被满足,且行驶总成本(总路径权重)最小。目标函数可以表示为:
min ∑ k ∑ ( v i , v j ) ∈ E k w ( i , j ) \min \sum_{k} \sum_{(v_i, v_j) \in E_k} w(i, j) mink∑(vi,vj)∈Ek∑w(i,j)
其中 E k E_k Ek 是分配给车辆 k k k 的路径边集。
5. 路径的约束:
- 每辆车必须从配送中心 v 0 v_0 v0 出发,访问若干客户后,再返回配送中心。
- 每个客户节点 v i v_i vi 只能被一次性访问。
- 每辆车的行驶路径需要确保所有客户都被服务。
综上:
CVRP问题可以用一个有向加权图 G = ( V , E ) G = (V, E) G=(V,E) 来表示,其中每条边附带的权重代表行驶代价,并结合车辆的容量约束,寻找满足所有客户需求且最小化总行驶代价的路径集合。
代码(总)
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
# 生成加权有向图表示CVRP问题
def generate_cvrp_graph(num_customers, depot_pos=(0, 0), max_demand=10, max_distance=100):
# 创建有向图
G = nx.DiGraph()
# 添加配送中心 (depot)
G.add_node(0, pos=depot_pos, demand=0)
# 随机生成客户节点的位置和需求
np.random.seed(42) # 保持随机性可重复
for i in range(1, num_customers + 1):
pos = (np.random.uniform(-max_distance, max_distance), np.random.uniform(-max_distance, max_distance))
demand = np.random.randint(1, max_demand)
G.add_node(i, pos=pos, demand=demand)
# 计算节点之间的欧几里得距离作为边权重
for i in G.nodes:
for j in G.nodes:
if i != j:
pos_i = G.nodes[i]['pos']
pos_j = G.nodes[j]['pos']
distance = np.linalg.norm(np.array(pos_i) - np.array(pos_j)) # 欧几里得距离
G.add_edge(i, j, weight=distance)
return G
# 绘制CVRP问题的图
def draw_cvrp_graph(G):
pos = nx.get_node_attributes(G, 'pos')
labels = {i: f"{i}\n(D:{G.nodes[i]['demand']})" for i in G.nodes}
edge_labels = {(i, j): f"{G.edges[i, j]['weight']:.1f}" for i, j in G.edges}
# 绘制节点和边
nx.draw(G, pos, with_labels=True, labels=labels, node_color='lightblue', node_size=700, font_size=10, font_weight='bold')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_color='red')
plt.title('CVRP Problem - Graph Representation')
plt.show()
# 生成并绘制CVRP问题图(假设有5个客户)
G = generate_cvrp_graph(num_customers=5)
draw_cvrp_graph(G)

# 生成加权有向图表示CVRP问题
def generate_cvrp_graph(num_customers, depot_pos=(0, 0), max_demand=10, max_distance=100):
# 创建有向图
G = nx.DiGraph()
# 添加配送中心 (depot)
G.add_node(0, pos=depot_pos, demand=0)
# 随机生成客户节点的位置和需求
np.random.seed(42) # 保持随机性可重复
for i in range(1, num_customers + 1):
pos = (np.random.uniform(-max_distance, max_distance), np.random.uniform(-max_distance, max_distance))
demand = np.random.randint(1, max_demand)
G.add_node(i, pos=pos, demand=demand)
# 计算节点之间的欧几里得距离作为边权重
for i in G.nodes:
for j in G.nodes:
if i != j:
pos_i = G.nodes[i]['pos']
pos_j = G.nodes[j]['pos']
distance = np.linalg.norm(np.array(pos_i) - np.array(pos_j)) # 欧几里得距离
G.add_edge(i, j, weight=distance)
return G
generate_cvrp_graph 函数详解
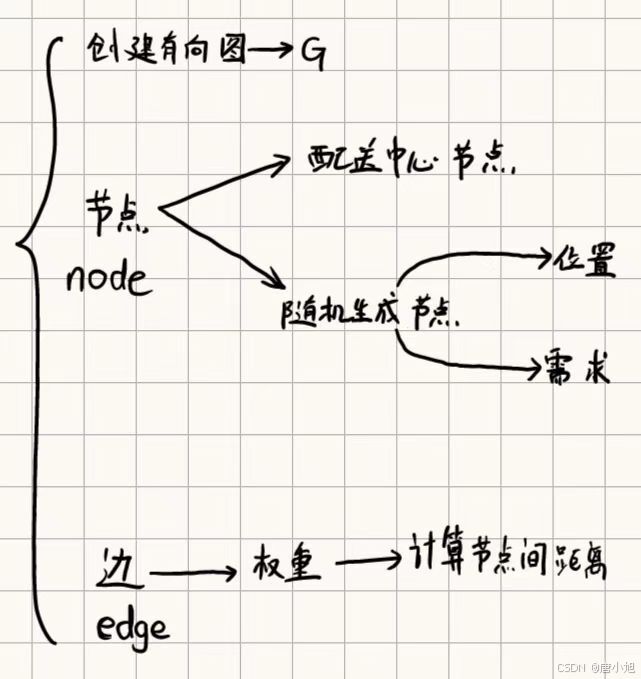
这个函数 generate_cvrp_graph 用于生成一个加权有向图,模拟了容量约束车辆路径问题(CVRP)中的配送中心和客户位置及其需求。我们逐步解析这个函数的每一部分:
1. 函数定义和输入参数
def generate_cvrp_graph(num_customers, depot_pos=(0, 0), max_demand=10, max_distance=100):
num_customers:表示要生成的客户数量。depot_pos:配送中心的位置,默认为原点(0, 0)。max_demand:每个客户的最大需求量,需求将在1和max_demand之间随机生成。max_distance:客户节点位置的随机范围,每个客户的坐标将在[-max_distance, max_distance]的范围内随机生成。
2. 创建有向图
G = nx.DiGraph()
这里,nx.DiGraph() 是 NetworkX 中用于生成有向图的函数。有向图意味着图中的边是有方向的,这在车辆路径问题中很重要,因为路径的方向和距离可能会不同(例如,从配送中心到客户和从客户返回的路程不同)。
3. 添加配送中心节点
G.add_node(0, pos=depot_pos, demand=0)
- 这里将配送中心作为图中的第一个节点 (
0) 添加。 pos=depot_pos:指定配送中心的位置(默认为原点(0, 0))。demand=0:配送中心没有需求,因此它的需求被设定为0。
4. 随机生成客户节点的位置和需求
np.random.seed(42) # 保持随机性可重复
for i in range(1, num_customers + 1):
pos = (np.random.uniform(-max_distance, max_distance), np.random.uniform(-max_distance, max_distance))
demand = np.random.randint(1, max_demand)
G.add_node(i, pos=pos, demand=demand)
- 通过
np.random.seed(42)保证生成的随机数是可重复的,便于调试和结果复现。 - 循环生成客户节点:
- 对于每一个客户,生成其位置和需求。客户的编号从
1开始。 pos = (np.random.uniform(-max_distance, max_distance), np.random.uniform(-max_distance, max_distance)):客户的位置由均匀分布的随机数生成,范围为[-max_distance, max_distance]。demand = np.random.randint(1, max_demand):客户的需求是随机整数,范围为[1, max_demand),也就是说,客户的需求至少为1。
- 对于每一个客户,生成其位置和需求。客户的编号从
5. 计算节点之间的欧几里得距离并作为边权重
for i in G.nodes:
for j in G.nodes:
if i != j:
pos_i = G.nodes[i]['pos']
pos_j = G.nodes[j]['pos']
distance = np.linalg.norm(np.array(pos_i) - np.array(pos_j)) # 欧几里得距离
G.add_edge(i, j, weight=distance)
- 这是一个嵌套循环,遍历图中所有节点的两两组合。对于每一对不同的节点 i i i 和 j j j,计算它们之间的距离。
- 节点之间的欧几里得距离:
pos_i = G.nodes[i]['pos']:提取节点 i i i 的位置。pos_j = G.nodes[j]['pos']:提取节点 j j j 的位置。distance = np.linalg.norm(np.array(pos_i) - np.array(pos_j)):使用numpy的linalg.norm函数计算两个位置之间的欧几里得距离。
- 将距离添加为图中的边的权重:
G.add_edge(i, j, weight=distance):在节点 i i i 和 j j j 之间添加一条有向边,并将计算出来的距离作为该边的权重。这表示车辆从一个节点到另一个节点的行驶距离。
6. 返回生成的图
return G
函数返回生成的加权有向图 G,其中包括配送中心和客户节点,它们的位置和需求都已经设定,同时每一对节点之间的距离已经计算并作为边的权重。
总结:
- 该函数生成一个加权有向图来表示容量约束车辆路径问题(CVRP)。
- 图中包含一个配送中心和多个客户节点,每个节点有各自的需求和随机位置。
- 节点之间的边表示车辆可能的路径,边的权重(距离)根据节点之间的欧几里得距离计算。
# 绘制CVRP问题的图
def draw_cvrp_graph(G):
pos = nx.get_node_attributes(G, 'pos')
labels = {i: f"{i}\n(D:{G.nodes[i]['demand']})" for i in G.nodes}
edge_labels = {(i, j): f"{G.edges[i, j]['weight']:.1f}" for i, j in G.edges}
# 绘制节点和边
nx.draw(G, pos, with_labels=True, labels=labels, node_color='lightblue', node_size=700, font_size=10, font_weight='bold')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_color='red')
plt.title('CVRP Problem - Graph Representation')
plt.show()
draw_cvrp_graph 函数详解
此函数用于绘制CVRP问题的图,即将图中的配送中心、客户节点及其需求,以及它们之间的路径与距离显示出来。
函数定义
def draw_cvrp_graph(G):
- 参数:
G是一个由NetworkX构建的有向图,其中包含配送中心和客户节点及它们之间的路径。
1. 获取节点位置和标签
pos = nx.get_node_attributes(G, 'pos')
labels = {i: f"{i}\n(D:{G.nodes[i]['demand']})" for i in G.nodes}
edge_labels = {(i, j): f"{G.edges[i, j]['weight']:.1f}" for i, j in G.edges}
pos:从图G中提取每个节点的坐标位置,这些位置在创建图时已存储在节点的'pos'属性中。labels:为每个节点生成标签。标签格式为:
例如,节点编号 (D:需求)"1\n(D:5)"表示节点编号为1,其需求为5。edge_labels:为每条边生成标签,表示边的权重(路径距离)。使用f"{G.edges[i, j]['weight']:.1f}"格式化距离,只保留一位小数。例如,如果权重是10.457,则标签显示为10.5。
2. 绘制图形
nx.draw(G, pos, with_labels=True, labels=labels, node_color='lightblue', node_size=700, font_size=10, font_weight='bold')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_color='red')
-
nx.draw:- 绘制节点和边。
pos:节点的位置。with_labels=True:在节点上显示标签。labels=labels:使用自定义的标签(显示节点编号和需求)。node_color='lightblue':节点颜色为浅蓝色。node_size=700:节点的大小。font_size=10和font_weight='bold':设置标签字体大小和加粗。
-
nx.draw_networkx_edge_labels:- 在每条边上显示权重(距离)。
edge_labels=edge_labels:使用自定义的边标签。font_color='red':边标签的字体颜色为红色。
3. 添加标题并显示图形
plt.title('CVRP Problem - Graph Representation')
plt.show()
plt.title:设置图形标题为'CVRP Problem - Graph Representation'。plt.show:显示绘制的图形。
总结
- 该函数通过
NetworkX和Matplotlib绘制了一个带有节点、边和标签的CVRP图。 - 节点标签显示了客户编号及其需求,边标签显示了路径距离(边的权重)。
- 配送中心和客户之间的所有可能路径都在图中清晰展示,帮助分析最优的路径选择。
此函数的目的是将CVRP问题的结构以可视化形式呈现,便于观察和理解配送中心与客户之间的关系及路径代价。
总结
提示:这里对文章进行总结:
例如:以上就是今天要讲的内容,本文仅仅简单介绍了pandas的使用,而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。























 788
788

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








