机器学习数学基础(三)
(一)矩阵
引例SVD
什么是SVD?
奇异值分解(Singular Value Decomposition)是一种重要的矩阵分解方法,可以看作对称方阵在任意矩阵上的推广。
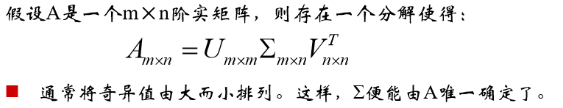
与特征值、特征向量概念相对应:
- ∑ \sum_{} ∑ 对角线上的元素称为矩阵A的奇异值
- U 的第i列称为A的关于 σ i \sigma_i σi的左奇异向量
- V 的第i列称为A的关于 σ i \sigma_i σi的右奇异向量
举例
-
已知 4 × 5 4 \times 5 4×5阶实矩阵A,求A的SVD分解:

-
一个图像也可以看作一个矩阵,进行分解

基础概念
定义
线性代数定义:方阵行列式
- 1阶方阵行列式是该元素本身
- n阶方阵行列式等于它任一行/列各元素与其对应的代数余子式乘积之和
代数余子式
- 余子式
在一个n阶行列式A中,把(i,j)元素 a i j a_ij aij所在的第i行和第j列划去后,留下的n-1阶方阵的行列式叫做元素 a i j a_ij aij的余子式,记作 M i j M_ij Mij - 代数余子式
代数余子式 A i j A_ij Aij = ( − 1 ) i + j (-1)^{i+j} (−1)i+j M i j M_ij Mij
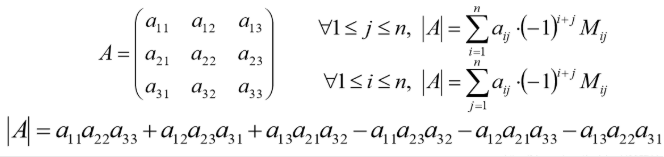
伴随矩阵
对于 n × n n \times n n×n方阵的任意元素 a i j a_ij aij都有各自的代数余子式 A i j A_ij Aij = ( − 1 ) i + j (-1)^{i+j} (−1)i+j M i j M_ij Mij,
构造 n × n n \times n n×n的方阵 A ∗ A^* A∗:

A ∗ A^* A∗是A的伴随矩阵
A i j A_ij Aij位于 A ∗ A^* A∗的第j行第i列
方阵的逆
A ⋅ A ∗ = ∣ A ∣ ⋅ I A\cdot A^*=|A|\cdot I A⋅A∗=∣A∣⋅I
推导过程如下:

范德蒙行列式
证明范德蒙行列式,使用数学归纳法

矩阵的乘法/状态转移矩阵
矩阵乘法
A为 m × s m \times s m×s阶矩阵,B为 s × n s \times n s×n阶矩阵,那么,C= A × B A \times B A×B阶矩阵是 m × n m \times n m×n阶矩阵,其中

矩阵和向量乘法
A为 m × n m \times n m×n阶矩阵,B为 n × 1 n \times 1 n×1阶矩阵,则 A x Ax Ax为 m × 1 m \times 1 m×1列向量,记为 y → = A ⋅ \overrightarrow{y} = A\cdot y=A⋅ x → \overrightarrow{x} x
由于n维列向量和n维空间的点一一对应,上式也是从n维空间的点到m维空间点的线性变换(旋转、平移)。
特殊的,若m=n,Ax完成的是n维空间内的线性变换。
应用:机械手臂移动
状态转移矩阵
-
状态转义概率
某随机过程,状态有n个,用1—n表示。记在当前时刻t时位于i状态,再t+1时刻位于j状态的概率为P(i,j)= P(j | i),即状态转移概率只依赖于前一个状态。

-
概率转移矩阵
第n+1代中处于第j个阶层的概率为:

此式中矩阵P为(条件)概率转移矩阵。第i行元素表示,在上一个状态为i时的分布概率,即:每一行元素和为1。 -
平稳分布
转移概率矩阵性质是初始概率不同,经过若干次迭代,最终稳定收敛在某个分布上,称为平稳分布,这个性质不是初始分布的性质。
以下两种写法等价:
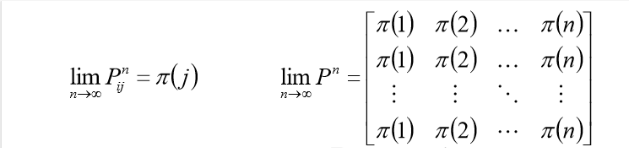
如果概率分布 π P = π \pi P = \pi πP=π,说明:
(1)该多项分布是状态转移矩阵P的平稳分布;
(2)线性方程xP = x的非负解为 π \pi π,而 P n P^n Pn唯一,因此 π \pi π是线性方程xP = x的唯一非负解
矩阵和向量组
矩阵的秩
设在矩阵A中有一个不等于零的r阶子式D,且所有r+1阶子式(若存在)为0,那么D为矩阵A的最高阶非零子式,r称为矩阵A的秩,记为 R ( A ) = r R(A)=r R(A)=r。
- n × n n \times n n×n的可逆矩阵,秩为n
- 可逆矩阵又称满秩矩阵
- 矩阵的秩等于它行(列)向量组的秩
秩和线性方程组解的关系

对于n元线性方程组 A x = b Ax = b Ax=b
- 无解的充要条件是 R ( A ) < R ( A , b ) R(A) < R(A,b) R(A)<R(A,b)
- 有唯一解的充要条件是 R ( A ) = R ( A , b ) = n R(A) = R(A,b) = n R(A)=R(A,b)=n
- 有无限多解的充要条件是 R ( A ) = R ( A , b ) < n R(A) = R(A,b) < n R(A)=R(A,b)<n
推论 - A x = 0 Ax = 0 Ax=0 有非零解的充要条件是 R ( A ) < n R(A) < n R(A)<n
- A x = b Ax = b Ax=b 有解的充要条件是 R ( A ) = R ( A , b ) R(A) = R(A,b) R(A)=R(A,b)
向量组等价
- 什么是向量组等价
向量 b → \overrightarrow{b} b能由向量组A: a 1 → \overrightarrow{a_1} a1, a 2 → \overrightarrow{a_2} a2,… a m → \overrightarrow{a_m} am线性表出的充要条件是矩阵A=( a 1 → \overrightarrow{a_1} a1, a 2 → \overrightarrow{a_2} a2,… a m → \overrightarrow{a_m} am)的秩等于矩阵B=( a 1 → \overrightarrow{a_1} a1, a 2 → \overrightarrow{a_2} a2,… a m → \overrightarrow{a_m} am, b → \overrightarrow{b} b)的秩
设有两个向量组A: a 1 → \overrightarrow{a_1} a1, a 2 → \overrightarrow{a_2} a2,… a m → \overrightarrow{a_m} am和B: b 1 → \overrightarrow{b_1} b1, b 2 → \overrightarrow{b_2} b








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章














 1048
1048











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








