文章目录
5 向量微积分(Vector Calculus)
机器学习中的许多算法是根据一组期望的模型参数来优化目标函数的(这些参数控制模型对数据的解释程度):找到好的参数可看作一个优化问题(见第8.2节和第8.3节)。例如:
(i)线性回归(见第9章),其中我们研究曲线拟合问题并优化线性权重参数以极大化似然;
(ii)用于降维和数据压缩的神经网络自编码器,其中参数是每层的权重和偏差,我们通过链式法则最小化重建损失;
(iii)高斯混合模型(见第11章)用于数据分布建模,在该模型中,我们优化了每个混合成分的位置和形状参数,以极大化模型的似然。

图 5.1向量微积分在(a)回归问题:找到参数,使曲线能很好地解释观察值。(b)高斯混合模型进行密度估计:求平均值和协方差,使得数据(点)可以被很好地解释。
图 5.1展示了其中一些方法,我们通常使用利用梯度信息的优化算法(7.2节)来解决这些问题。图 5.2概述了本章中的各个概念的关系,以及它们如何与本书的其他章节的联系。

图 5.2本章介绍的概念的思维导图,以及它们与其它章节的联系。
本章的核心是函数这一概念。函数 f f f是将两个量相互关联的量。在本书中,这两个量通常是输入 x ∈ R D \boldsymbol{x} \in \mathbb{R}^{D} x∈RD和目标(函数值) f ( x ) f(\boldsymbol{x}) f(x),如果没有其他说明,我们假设它们是实数。这里 R D \mathbb{R}^{D} RD是 f f f的定义域,函数值 f ( x ) f(\boldsymbol{x}) f(x)是 f f f的像/陪域。
2.7.3中,我们详细地讨论了线性函数。我们用
f
:
R
D
→
R
x
↦
f
(
x
)
\begin{aligned}f: \mathbb{R}^{D} & \rightarrow \mathbb{R} \\\boldsymbol{x} & \mapsto f(\boldsymbol{x})\end{aligned}
f:RDx→R↦f(x)
来表示函数,其中
R
D
→
R
\mathbb{R}^{D} \rightarrow \mathbb{R}
RD→R指定
f
f
f是从
R
D
\mathbb{R}^{D}
RD到
R
\mathbb{R}
R的映射,
x
↦
f
(
x
)
\boldsymbol{x} \mapsto f(\boldsymbol{x})
x↦f(x)指定输入
x
\boldsymbol{x}
x到函数值
f
(
x
)
f(\boldsymbol{x})
f(x)的显式赋值。函数
f
f
f为每个输入
x
\boldsymbol{x}
x指定一个函数值
f
(
x
)
f(\boldsymbol{x})
f(x)。
例 5.1
回忆一下,点积是内积(3.2节)的特例。函数
f
(
x
)
=
x
⊤
x
,
x
∈
R
2
f(\boldsymbol{x})=\boldsymbol{x}^{\top} \boldsymbol{x}, \boldsymbol{x} \in \mathbb{R}^{2}
f(x)=x⊤x,x∈R2用前面的符号表示为:
f
:
R
2
→
R
x
↦
x
1
2
+
x
2
2
\begin{aligned}f: \mathbb{R}^{2} & \rightarrow \mathbb{R} \\\boldsymbol{x} & \mapsto x_{1}^{2}+x_{2}^{2}\end{aligned}
f:R2x→R↦x12+x22
在这一章中,我们将讨论如何计算函数的梯度,这通常是机器学习模型的学习中必不可少的,因为梯度是朝着陡峭的方向上升的。因此,向量微积分是机器学习中重要的基本数学工具之一。在这本书中,我们假设函数都是可微的。使用一些在这里没有涵盖的附加技术定义,我们所提到的许多方法还可以扩展到次微分(sub-differentials,在某些点连续但不可微的函数)。我们将在第7章中研究函数约束。
5.1 单变量函数的微分
接下来,我们简要回顾一下单变量函数的微分,这可能是我们在高中就已经很熟悉的了。我们从一个单变量函数 y = f ( x ) , x , y ∈ R y=f(x), x, y \in \mathbb{R} y=f(x),x,y∈R的差商开始,然后用它来定义导数。
定义 5.1 差商
差商(Difference Quotient)
δ
y
δ
x
:
=
f
(
x
+
δ
x
)
−
f
(
x
)
δ
x
\frac{\delta y}{\delta x}:=\frac{f(x+\delta x)-f(x)}{\delta x}
δxδy:=δxf(x+δx)−f(x)
计算函数
f
f
f图形上通过两点的割线的斜率。图5.3展示的是两点的
x
x
x坐标分别为
x
0
x_0
x0和
x
0
+
δ
x
x_0+δx
x0+δx的情况。

图 5.3 函数
f
f
f在
x
0
x_0
x0和
x
0
+
δ
x
x_0+δ_x
x0+δx之间的平均斜率(average incline)是
f
(
x
0
)
f(x_0)
f(x0)和
f
(
x
0
+
δ
x
)
f(x_0+δ_x)
f(x0+δx)割线(蓝色)的斜率,由
δ
y
/
δ
x
δy/δx
δy/δx给出。
如果我们假设 f f f是线性函数,差商也可以被认为是 f f f在 x x x和 x + δ x x+δx x+δx之间的平均斜率( average slope)。在极限 δ x → 0 δx→0 δx→0下,如果 f f f是可微的,则得到 f f f在 x x x的正切(tangent)。正切就是 f f f关于 x x x的导数。
定义 5.2导数
更正式地说,对于
h
>
0
h\gt 0
h>0,
f
f
f在
x
x
x的导数(derivative)被定义为极限:
d
f
d
x
:
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
\frac{\mathrm{d} f}{\mathrm{~d} x}:=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}
dxdf:=h→0limhf(x+h)−f(x)
这样上面图5.3的割线也变成了切线。
f f f导数的方向指向 f f f最陡峭的上升方向。
例 5.2 多项式的导数
计算 f ( x ) = x n , n ∈ N f(x)=x^{n}, n \in \mathbb{N} f(x)=xn,n∈N的导数。我们可以很快得到答案是 n x n − 1 nx^{n−1} nxn−1,但是这里我们想用导数的定义推导这个结果
利用导数的定义,我们得到:
d
f
d
x
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
=
lim
h
→
0
(
x
+
h
)
n
−
x
n
h
=
lim
h
→
0
∑
i
=
0
n
(
n
i
)
x
n
−
i
h
i
−
x
n
h
.
\begin{aligned}\frac{\mathrm{d} f}{\mathrm{~d} x} &=\lim _{h \rightarrow 0} \frac{\textcolor{blue}{f(x+h)}-\textcolor{red}{f(x)}}{h} \\&=\lim _{h \rightarrow 0} \frac{\textcolor{blue}{(x+h)^{n}}-\textcolor{red}{x^{n}}}{h} \\&=\lim _{h \rightarrow 0} \frac{\textcolor{blue}{\sum_{i=0}^{n}\left(\begin{array}{l}n \\i\end{array}\right) x^{n-i} h^{i}}-\textcolor{red}{x^{n}}}{h} .\end{aligned}
dxdf=h→0limhf(x+h)−f(x)=h→0limh(x+h)n−xn=h→0limh∑i=0n(ni)xn−ihi−xn.
由于
x
n
=
(
n
0
)
x
n
−
0
h
0
\textcolor{red}{x^{n}}=\left(\begin{array}{c}n \\0\end{array}\right) x^{n-0} h^{0}
xn=(n0)xn−0h0,
x
n
x^n
xn项被消去,我们得到从
i
=
1
i=1
i=1开始求和的项
d
f
d
x
=
lim
h
→
0
∑
i
=
1
n
(
n
i
)
x
n
−
i
h
i
h
=
lim
l
→
0
∑
i
=
1
n
(
n
i
)
x
n
−
i
h
i
−
1
=
lim
h
→
0
(
n
1
)
x
n
−
1
+
∑
i
=
2
n
(
n
i
)
x
n
−
i
h
i
−
1
⏟
→
0
as
h
→
0
=
n
!
1
!
(
n
−
1
)
!
x
n
−
1
=
n
x
n
−
1
.
\begin{aligned}\frac{\mathrm{d} f}{\mathrm{~d} x} &=\lim _{h \rightarrow 0} \frac{\sum_{i=1}^{n}\left(\begin{array}{l}n \\i\end{array}\right) x^{n-i} h^{i}}{h} \\&=\lim _{l \rightarrow 0} \sum_{i=1}^{n}\left(\begin{array}{l}n \\i\end{array}\right) x^{n-i} h^{i-1} \\&=\lim _{h \rightarrow 0}\left(\begin{array}{l}n \\1\end{array}\right) x^{n-1}+\underbrace{\sum_{i=2}^{n}\left(\begin{array}{l}n \\i\end{array}\right) x^{n-i} h^{i-1}}_{\rightarrow 0 \text { as } h \rightarrow 0} \\&=\frac{n !}{1 !(n-1) !} x^{n-1}=n x^{n-1} .\end{aligned}
dxdf=h→0limh∑i=1n(ni)xn−ihi=l→0limi=1∑n(ni)xn−ihi−1=h→0lim(n1)xn−1+→0 as h→0
i=2∑n(ni)xn−ihi−1=1!(n−1)!n!xn−1=nxn−1.
我们常见的组合符号 C n m C_n^m Cnm也可写成 ( n m ) \left(\begin{array}{l}n\\m\end{array}\right) (nm)。
5.1.1 泰勒级数
泰勒级数是函数 f f f的无穷项和的表示。这些项是用 f f f的导数来确定的
定义 5.3泰勒多项式
f
:
R
→
R
f: \mathbb{R} \rightarrow \mathbb{R}
f:R→R的
n
n
n次泰勒多项式(Taylor polynomial)定义为
T
n
(
x
)
:
=
∑
k
=
0
n
f
(
k
)
(
x
0
)
k
!
(
x
−
x
0
)
k
T_{n}(x):=\sum_{k=0}^{n} \frac{f^{(k)}\left(x_{0}\right)}{k !}\left(x-x_{0}\right)^{k}
Tn(x):=k=0∑nk!f(k)(x0)(x−x0)k
其中
f
(
k
)
(
x
0
)
f^{(k)}(x_0)
f(k)(x0)是
f
f
f在
x
0
x_0
x0的第
k
k
k阶导(假设它存在),
f
(
k
)
(
x
0
)
k
!
\frac{f^{(k)}\left(x_{0}\right)}{k !}
k!f(k)(x0)是多项式的系数。
定义 5.4泰勒级数
对于一个平滑的函数
f
∈
C
∞
,
f
:
R
→
R
f \in \mathcal{C}^{\infty}, f: \mathbb{R} \rightarrow \mathbb{R}
f∈C∞,f:R→R(
f
∈
C
∞
f \in \mathcal{C}^{\infty}
f∈C∞表示
f
f
f连续且可微无穷多次。),
f
f
f在
x
0
x_0
x0的泰勒级数(Taylor series)定义为:
T
∞
(
x
)
=
∑
k
=
0
∞
f
(
k
)
(
x
0
)
k
!
(
x
−
x
0
)
k
T_{\infty}(x)=\sum_{k=0}^{\infty} \frac{f^{(k)}\left(x_{0}\right)}{k !}\left(x-x_{0}\right)^{k}
T∞(x)=k=0∑∞k!f(k)(x0)(x−x0)k
当 x 0 = 0 x_0=0 x0=0时,我们得到麦克劳林级数(Maclaurin series)这一泰勒级数的特殊实例。如果 f ( x ) = T ∞ ( x ) f(x)=T_{\infty}(x) f(x)=T∞(x),那么 f f f称为解析的(analytic)。
备注:
一般来说,
n
n
n次泰勒多项式是非多项式函数的近似值。它在
x
0
x_0
x0附近与
f
f
f相似。然而,
n
n
n次泰勒多项式用
k
≤
n
k\le n
k≤n次多项式表示
f
f
f已经足够精确了,因为导数
f
(
i
)
,
i
>
k
f^{(i)}, i>k
f(i),i>k可能为0。
例 5.3 泰勒多项式
已知多项式:
f
(
x
)
=
x
4
f(x)=x^{4}
f(x)=x4
求在
x
0
=
1
x_0=1
x0=1的泰勒多项式
T
6
T_6
T6。我们首先计算系数
f
(
k
)
(
1
)
f^{(k)}(1)
f(k)(1),
k
=
0
,
…
,
6
:
k=0, \ldots, 6:
k=0,…,6:
f
(
1
)
=
1
f
′
(
1
)
=
4
f
′
′
(
1
)
=
12
f
(
3
)
(
1
)
=
24
f
(
4
)
(
1
)
=
24
f
(
5
)
(
1
)
=
0
f
(
6
)
(
1
)
=
0
\begin{aligned}f(1) &=1 \\f^{\prime}(1) &=4 \\f^{\prime \prime}(1) &=12 \\f^{(3)}(1) &=24 \\f^{(4)}(1) &=24 \\f^{(5)}(1) &=0 \\f^{(6)}(1) &=0\end{aligned}
f(1)f′(1)f′′(1)f(3)(1)f(4)(1)f(5)(1)f(6)(1)=1=4=12=24=24=0=0
因此,期望的泰勒多项式是
T
6
(
x
)
=
∑
k
=
0
6
f
(
k
)
(
x
0
)
k
!
(
x
−
x
0
)
k
=
1
+
4
(
x
−
1
)
+
6
(
x
−
1
)
2
+
4
(
x
−
1
)
3
+
(
x
−
1
)
4
+
0
\begin{aligned}T_{6}(x) &=\sum_{k=0}^{6} \frac{f^{(k)}\left(x_{0}\right)}{k !}\left(x-x_{0}\right)^{k} \\&=1+4(x-1)+6(x-1)^{2}+4(x-1)^{3}+(x-1)^{4}+0\end{aligned}
T6(x)=k=0∑6k!f(k)(x0)(x−x0)k=1+4(x−1)+6(x−1)2+4(x−1)3+(x−1)4+0
展开并重新排列:
T
6
(
x
)
=
(
1
−
4
+
6
−
4
+
1
)
+
x
(
4
−
12
+
12
−
4
)
+
x
2
(
6
−
12
+
6
)
+
x
3
(
4
−
4
)
+
x
4
=
x
4
=
f
(
x
)
\begin{aligned}T_{6}(x)=&(1-4+6-4+1)+x(4-12+12-4) \\&+x^{2}(6-12+6)+x^{3}(4-4)+x^{4} \\=& x^{4}=f(x)\end{aligned}
T6(x)==(1−4+6−4+1)+x(4−12+12−4)+x2(6−12+6)+x3(4−4)+x4x4=f(x)
我们得到了原函数的精确表示。
例 5.4 泰勒级数
考虑函数
f
(
x
)
=
sin
(
x
)
+
cos
(
x
)
∈
C
∞
f(x)=\sin (x)+\cos (x) \in \mathcal{C}^{\infty}
f(x)=sin(x)+cos(x)∈C∞
我们寻求
f
f
f在
x
0
=
0
x_0=0
x0=0的泰勒级数展开式,这是
f
f
f的麦克劳林级数展开式。我们得到以下导数:
f
(
0
)
=
sin
(
0
)
+
cos
(
0
)
=
1
f
′
(
0
)
=
cos
(
0
)
−
sin
(
0
)
=
1
f
′
′
(
0
)
=
−
sin
(
0
)
−
cos
(
0
)
=
−
1
f
(
3
)
(
0
)
=
−
cos
(
0
)
+
sin
(
0
)
=
−
1
f
(
4
)
(
0
)
=
sin
(
0
)
+
cos
(
0
)
=
f
(
0
)
=
1
.
.
.
\begin{aligned}f(0) &=\sin (0)+\cos (0)=1 \\f^{\prime}(0) &=\cos (0)-\sin (0)=1 \\f^{\prime \prime}(0) &=-\sin (0)-\cos (0)=-1 \\f^{(3)}(0) &=-\cos (0)+\sin (0)=-1 \\f^{(4)}(0) &=\sin (0)+\cos (0)=f(0)=1\\...\end{aligned}
f(0)f′(0)f′′(0)f(3)(0)f(4)(0)...=sin(0)+cos(0)=1=cos(0)−sin(0)=1=−sin(0)−cos(0)=−1=−cos(0)+sin(0)=−1=sin(0)+cos(0)=f(0)=1
我们可以在这里看到一个模式:泰勒级数中的系数只有 ± 1 ±1 ±1(因为 s i n ( 0 ) = 0 sin(0)=0 sin(0)=0),每个系数在切换到另一个之前出现两次。此外, f ( k + 4 ) ( 0 ) = f ( k ) ( 0 ) f^{(k+4)}(0)=f^{(k)}(0) f(k+4)(0)=f(k)(0)。
因此,
f
f
f在
x
0
=
0
x_0=0
x0=0处的整个泰勒级数展开为:
T
∞
(
x
)
=
∑
k
=
0
∞
f
(
k
)
(
x
0
)
k
!
(
x
−
x
0
)
k
=
1
+
x
−
1
2
!
x
2
−
1
3
!
x
3
+
1
4
!
x
4
+
1
5
!
x
5
−
⋯
=
1
−
1
2
!
x
2
+
1
4
!
x
4
∓
⋯
+
x
−
1
3
!
x
3
+
1
5
!
x
5
∓
⋯
=
∑
k
=
0
∞
(
−
1
)
k
1
(
2
k
)
!
x
2
k
+
∑
k
=
0
∞
(
−
1
)
k
1
(
2
k
+
1
)
!
x
2
k
+
1
=
cos
(
x
)
+
sin
(
x
)
\begin{aligned}T_{\infty}(x) &=\sum_{k=0}^{\infty} \frac{f^{(k)}\left(x_{0}\right)}{k !}\left(x-x_{0}\right)^{k} \\&=1+x-\frac{1}{2 !} x^{2}-\frac{1}{3 !} x^{3}+\frac{1}{4 !} x^{4}+\frac{1}{5 !} x^{5}-\cdots \\&=\textcolor{orange}{1-\frac{1}{2 !} x^{2}+\frac{1}{4 !} x^{4} \mp \cdots}+\textcolor{blue}{x-\frac{1}{3 !} x^{3}+\frac{1}{5 !} x^{5} \mp \cdots} \\&=\textcolor{orange}{\sum_{k=0}^{\infty}(-1)^{k} \frac{1}{(2 k) !} x^{2 k}}+\textcolor{blue}{\sum_{k=0}^{\infty}(-1)^{k} \frac{1}{(2 k+1) !} x^{2 k+1} }\\&=\textcolor{orange}{\cos (x)}+\textcolor{blue}{\sin (x)}\end{aligned}
T∞(x)=k=0∑∞k!f(k)(x0)(x−x0)k=1+x−2!1x2−3!1x3+4!1x4+5!1x5−⋯=1−2!1x2+4!1x4∓⋯+x−3!1x3+5!1x5∓⋯=k=0∑∞(−1)k(2k)!1x2k+k=0∑∞(−1)k(2k+1)!1x2k+1=cos(x)+sin(x)
其中我们使用了幂级数展开:
cos
(
x
)
=
∑
k
=
0
∞
(
−
1
)
k
1
(
2
k
)
!
x
2
k
\cos (x)=\sum_{k=0}^{\infty}(-1)^{k} \frac{1}{(2 k) !} x^{2 k}
cos(x)=k=0∑∞(−1)k(2k)!1x2k
sin
(
x
)
=
∑
k
=
0
∞
(
−
1
)
k
1
(
2
k
+
1
)
!
x
2
k
+
1
\sin (x)=\sum_{k=0}^{\infty}(-1)^{k} \frac{1}{(2 k+1) !} x^{2 k+1}
sin(x)=k=0∑∞(−1)k(2k+1)!1x2k+1
图5.4显示了 n = 0 、 1 、 5 、 10 n=0、1、5、10 n=0、1、5、10时对应的泰勒多项式 T n T_n Tn以及 f f f。
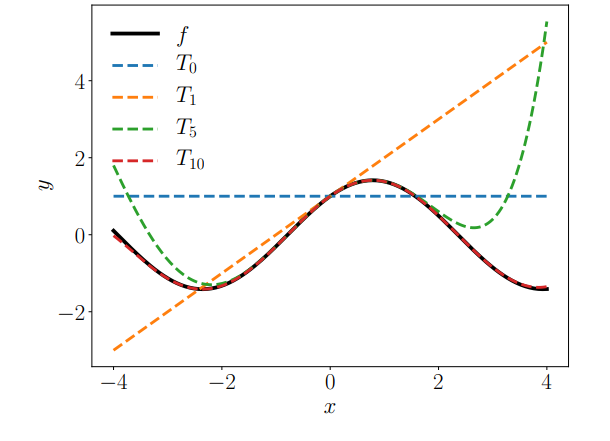
图 5.4泰勒多项式。原函数
f
(
x
)
=
s
i
n
(
x
)
+
c
o
s
(
x
)
f(x) = sin(x) + cos(x)
f(x)=sin(x)+cos(x)(黑色,实心)在
x
0
=
0
x_0 = 0
x0=0附近用泰勒多项式(虚线)逼近。高阶泰勒多项式能更好地逼近函数
f
f
f。
T
10
T_{10}
T10在
[
−
4
,
4
]
[−4,4]
[−4,4]中已经与
f
f
f很相似了。
备注:
泰勒级数是幂级数的特例,幂级数表达式为:
f
(
x
)
=
∑
k
=
0
∞
a
k
(
x
−
c
)
k
f(x)=\sum_{k=0}^{\infty} a_{k}(x-c)^{k}
f(x)=k=0∑∞ak(x−c)k
其中 a k a_k ak为系数, c c c为常数。定义5.4中的式子是它的特殊形式。
5.1.2 微分法则
下面,我们用 f ′ f' f′表示 f f f的导数,简要地说明基本的微分规则:
乘积法则:
(
f
(
x
)
g
(
x
)
)
′
=
f
′
(
x
)
g
(
x
)
+
f
(
x
)
g
′
(
x
)
(f(x) g(x))^{\prime}=f^{\prime}(x) g(x)+f(x) g^{\prime}(x)
(f(x)g(x))′=f′(x)g(x)+f(x)g′(x)
除法法则:
(
f
(
x
)
g
(
x
)
)
′
=
f
′
(
x
)
g
(
x
)
−
f
(
x
)
g
′
(
x
)
(
g
(
x
)
)
2
\left(\frac{f(x)}{g(x)}\right)^{\prime}=\frac{f^{\prime}(x) g(x)-f(x) g^{\prime}(x)}{(g(x))^{2}}
(g(x)f(x))′=(g(x))2f′(x)g(x)−f(x)g′(x)
加法法则:
(
f
(
x
)
+
g
(
x
)
)
′
=
f
′
(
x
)
+
g
′
(
x
)
(f(x)+g(x))^{\prime}=f^{\prime}(x)+g^{\prime}(x)
(f(x)+g(x))′=f′(x)+g′(x)
链式法则:
(
g
(
f
(
x
)
)
)
′
=
(
g
∘
f
)
′
(
x
)
=
g
′
(
f
(
x
)
)
f
′
(
x
)
(g(f(x)))^{\prime}=(g \circ f)^{\prime}(x)=g^{\prime}(f(x)) f^{\prime}(x)
(g(f(x)))′=(g∘f)′(x)=g′(f(x))f′(x)
这里,
g
∘
f
g \circ f
g∘f表示函数复合:
x
↦
f
(
x
)
↦
g
(
f
(
x
)
)
x \mapsto f(x) \mapsto g(f(x))
x↦f(x)↦g(f(x))
例 5.5 链式法则
让我们用链式法则计算函数
h
(
x
)
=
(
2
x
+
1
)
4
h(x)=(2 x+1)^{4}
h(x)=(2x+1)4的导数
h
(
x
)
=
(
2
x
+
1
)
4
=
g
(
f
(
x
)
)
f
(
x
)
=
2
x
+
1
(
5.34
)
g
(
f
)
=
f
4
\begin{array}{l}h(x)=(2 x+1)^{4}=g(f(x)) \\f(x)=2 x+1 \qquad(5.34)\\g(f)=f^{4}\end{array}
h(x)=(2x+1)4=g(f(x))f(x)=2x+1(5.34)g(f)=f4
我们得到了
f
f
f和
g
g
g的导数为:
f
′
(
x
)
=
2
g
′
(
f
)
=
4
f
3
\begin{array}{l}f^{\prime}(x)=2 \\g^{\prime}(f)=4 f^{3}\end{array}
f′(x)=2g′(f)=4f3
使得
h
h
h的导数为:
h ′ ( x ) = g ′ ( f ) f ′ ( x ) = ( 4 f 3 ) ⋅ 2 = ( 5.34 ) 4 ( 2 x + 1 ) 3 ⋅ 2 = 8 ( 2 x + 1 ) 3 h^{\prime}(x)=g^{\prime}(f) f^{\prime}(x)=\left(4 f^{3}\right) \cdot 2 \stackrel{(5.34)}{=} 4(2 x+1)^{3} \cdot 2=8(2 x+1)^{3} h′(x)=g′(f)f′(x)=(4f3)⋅2=(5.34)4(2x+1)3⋅2=8(2x+1)3
5.2 偏微分与梯度
第5.1节中讨论的微分只适用于一个标量变量 x ∈ R x \in \mathbb{R} x∈R的函数 f f f。在下面,我们考虑函数 f f f包含一个或多个变量x∈Rn的一般情况,例如, f ( x ) = f ( x 1 , x 2 ) f(\boldsymbol{x})=f\left(x_{1}, x_{2}\right) f(x)=f(x1,x2)。导数对多变量函数的推广是梯度(gradient)。
我们通过一次改变一个变量并保持其他变量不变来求函数 f f f相对于 x x x的偏导数。梯度就是这些偏导数(partial derivatives)构成的的集合。
定义 5.5偏导数
对于有
n
n
n个变量
x
1
,
…
,
x
n
x_{1}, \ldots, x_{n}
x1,…,xn的函数
f
:
R
n
→
R
,
x
↦
f
(
x
)
,
x
∈
R
n
f: \mathbb{R}^{n} \rightarrow \mathbb{R}, \boldsymbol{x} \mapsto f(\boldsymbol{x}), \boldsymbol{x} \in \mathbb{R}^{n}
f:Rn→R,x↦f(x),x∈Rn,我们定义偏导数为:
∂
f
∂
x
1
=
lim
h
→
0
f
(
x
1
+
h
,
x
2
,
…
,
x
n
)
−
f
(
x
)
h
⋮
∂
f
∂
x
n
=
lim
h
→
0
f
(
x
1
,
…
,
x
n
−
1
,
x
n
+
h
)
−
f
(
x
)
h
(
5.39
)
\begin{aligned}\frac{\partial f}{\partial x_{1}} &=\lim _{h \rightarrow 0} \frac{f\left(x_{1}+h, x_{2}, \ldots, x_{n}\right)-f(\boldsymbol{x})}{h} \\& \vdots \\\frac{\partial f}{\partial x_{n}} &=\lim _{h \rightarrow 0} \frac{f\left(x_{1}, \ldots, x_{n-1}, x_{n}+h\right)-f(\boldsymbol{x})}{h}\end{aligned}\qquad (5.39)
∂x1∂f∂xn∂f=h→0limhf(x1+h,x2,…,xn)−f(x)⋮=h→0limhf(x1,…,xn−1,xn+h)−f(x)(5.39)
将它们组成一个行向量:
∇
x
f
=
grad
f
=
d
f
d
x
=
[
∂
f
(
x
)
∂
x
1
∂
f
(
x
)
∂
x
2
⋯
∂
f
(
x
)
∂
x
n
]
∈
R
1
×
n
(
5.40
)
\nabla_{\boldsymbol{x}} f=\operatorname{grad} f=\frac{\mathrm{d} f}{\mathrm{~d} \boldsymbol{x}}=\left[\begin{array}{cccc}\frac{\partial f(\boldsymbol{x})}{\partial x_{1}} & \frac{\partial f(\boldsymbol{x})}{\partial x_{2}} & \cdots & \frac{\partial f(\boldsymbol{x})}{\partial x_{n}}\end{array}\right] \in \mathbb{R}^{1 \times n} \qquad (5.40)
∇xf=gradf= dxdf=[∂x1∂f(x)∂x2∂f(x)⋯∂xn∂f(x)]∈R1×n(5.40)
其中 n n n是变量个数,1是 f f f的像/值域/陪域的维数。这里,我们定义了列向量 x = [ x 1 , … , x n ] ⊤ ∈ R n \boldsymbol{x}=\left[x_{1}, \ldots, x_{n}\right]^{\top}\in \mathbb{R}^n x=[x1,…,xn]⊤∈Rn。(5.40)中的行向量称为 f f f的梯度(gradient)或雅可比矩阵(Jacobian),是第5.1节中导数的推广。
备注:
这种雅可比矩阵的定义是一般雅可比矩阵的特例,一般雅可比矩阵是对向量值函数(vector-valued function)定义的。我们将在第5.3节谈到这一点。
例 5.6偏导数的链式法则
对于
f
(
x
,
y
)
=
(
x
+
2
y
3
)
2
f(x, y)=\left(x+2 y^{3}\right)^{2}
f(x,y)=(x+2y3)2,我们求其偏微分:
∂
f
(
x
,
y
)
∂
x
=
2
(
x
+
2
y
3
)
∂
∂
x
(
x
+
2
y
3
)
=
2
(
x
+
2
y
3
)
\frac{\partial f(x, y)}{\partial x}=2\left(x+2 y^{3}\right) \frac{\partial}{\partial x}\left(x+2 y^{3}\right)=2\left(x+2 y^{3}\right)
∂x∂f(x,y)=2(x+2y3)∂x∂(x+2y3)=2(x+2y3)
∂
f
(
x
,
y
)
∂
y
=
2
(
x
+
2
y
3
)
∂
∂
y
(
x
+
2
y
3
)
=
12
(
x
+
2
y
3
)
y
2
\frac{\partial f(x, y)}{\partial y}=2\left(x+2 y^{3}\right) \frac{\partial}{\partial y}\left(x+2 y^{3}\right)=12\left(x+2 y^{3}\right) y^{2}
∂y∂f(x,y)=2(x+2y3)∂y∂(x+2y3)=12(x+2y3)y2
其中我们使用了链式法则计算。
备注(梯度用行向量表示)。
向量通常用列向量表示,将梯度向量定义为列向量在文献中并不少见。我们将梯度向量定义为行向量的原因有两个:
首先,我们可以一致地将梯度推广到向量值函数 f : R n → R m f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m} f:Rn→Rm(然后梯度变成矩阵)。其次,我们可以很方便地应用多变量链式法则,而不必注意梯度的维数。我们将在第5.3节讨论这两点。
例 5.7 梯度 (Gradient)
对于
f
(
x
1
,
x
2
)
=
x
1
2
x
2
+
x
1
x
2
3
∈
R
f\left(x_{1}, x_{2}\right)=x_{1}^{2} x_{2}+x_{1} x_{2}^{3} \in \mathbb{R}
f(x1,x2)=x12x2+x1x23∈R,其偏导数为:
∂
f
(
x
1
,
x
2
)
∂
x
1
=
2
x
1
x
2
+
x
2
3
\frac{\partial f\left(x_{1}, x_{2}\right)}{\partial x_{1}}=2 x_{1} x_{2}+x_{2}^{3}
∂x1∂f(x1,x2)=2x1x2+x23
∂
f
(
x
1
,
x
2
)
∂
x
2
=
x
1
2
+
3
x
1
x
2
2
\frac{\partial f\left(x_{1}, x_{2}\right)}{\partial x_{2}}=x_{1}^{2}+3 x_{1} x_{2}^{2}
∂x2∂f(x1,x2)=x12+3x1x22
那么其梯度为
d
f
d
x
=
[
∂
f
(
x
1
,
x
2
)
∂
x
1
∂
f
(
x
1
,
x
2
)
∂
x
2
]
=
[
2
x
1
x
2
+
x
2
3
x
1
2
+
3
x
1
x
2
2
]
∈
R
1
×
2
\frac{\mathrm{d} f}{\mathrm{~d} \boldsymbol{x}}=\left[\frac{\partial f\left(x_{1}, x_{2}\right)}{\partial x_{1}} \quad \frac{\partial f\left(x_{1}, x_{2}\right)}{\partial x_{2}}\right]=\left[2 x_{1} x_{2}+x_{2}^{3} \quad x_{1}^{2}+3 x_{1} x_{2}^{2}\right] \in \mathbb{R}^{1 \times 2}
dxdf=[∂x1∂f(x1,x2)∂x2∂f(x1,x2)]=[2x1x2+x23x12+3x1x22]∈R1×2
5.2.1 偏微分的基本法则
对于多变量
x
∈
R
n
\boldsymbol{x} \in \mathbb{R}^{n}
x∈Rn的情况下,我们从学校知道的基本微分法则(如加法法则、乘法法则、链式法则;另见第5.1.2节)仍然适用。然而,当我们计算关于向量
x
∈
R
n
\boldsymbol{x} \in \mathbb{R}^{n}
x∈Rn的导数时,我们需要注意:梯度现在涉及到向量和矩阵,而矩阵乘法是不可交换的(第2.2.1节)。
以下是一般的乘法法则、加法法则和链式法则:
乘法法则
∂
∂
x
(
f
(
x
)
g
(
x
)
)
=
∂
f
∂
x
g
(
x
)
+
f
(
x
)
∂
g
∂
x
\frac{\partial}{\partial \boldsymbol{x}}(f(\boldsymbol{x}) g(\boldsymbol{x}))=\frac{\partial f}{\partial \boldsymbol{x}} g(\boldsymbol{x})+f(\boldsymbol{x}) \frac{\partial g}{\partial \boldsymbol{x}}
∂x∂(f(x)g(x))=∂x∂fg(x)+f(x)∂x∂g
加法法则
∂
∂
x
(
f
(
x
)
+
g
(
x
)
)
=
∂
f
∂
x
+
∂
g
∂
x
\frac{\partial}{\partial \boldsymbol{x}}(f(\boldsymbol{x})+g(\boldsymbol{x}))=\frac{\partial f}{\partial \boldsymbol{x}}+\frac{\partial g}{\partial \boldsymbol{x}}
∂x∂(f(x)+g(x))=∂x∂f+∂x∂g
链式法则
∂
∂
x
(
g
∘
f
)
(
x
)
=
∂
∂
x
(
g
(
f
(
x
)
)
)
=
∂
g
∂
f
∂
f
∂
x
\frac{\partial}{\partial \boldsymbol{x}}(g \circ f)(\boldsymbol{x})=\frac{\partial}{\partial \boldsymbol{x}}(g(f(\boldsymbol{x})))=\frac{\partial g}{\partial f} \frac{\partial f}{\partial \boldsymbol{x}}
∂x∂(g∘f)(x)=∂x∂(g(f(x)))=∂f∂g∂x∂f
让我们仔细看看链式法则。链式法则在某种程度上类似于矩阵乘法的规则,即我们所说的两矩阵相邻维度必须匹配才能定义矩阵乘法;参见第2.2.1节。如果我们从左到右,链式法则显示出与矩阵乘法相似的性质: ∂ f ∂f ∂f出现在第一个因子的“分母”(类似于矩阵乘法第一个矩阵的列数)和第二个因子的“分子”中(相当于矩阵乘法中第二个矩阵的行数)。如果我们将这些因子相乘,这样的乘法是有定义的,即 ∂ f ∂f ∂f的维数匹配, ∂ f ∂f ∂f被“消去”,留下 ∂ g / ∂ x ∂g/∂x ∂g/∂x。
这只是一种直观解释,但在数学上并不正确,因为偏导数不是分数。
5.2.2 链式法则
考虑两个变量
x
1
x_1
x1,
x
2
x_2
x2的函数
f
:
R
2
→
R
f: \mathbb{R}^{2} \rightarrow \mathbb{R}
f:R2→R。此外,
x
1
(
t
)
x_1(t)
x1(t)和
x
2
(
t
)
x_2(t)
x2(t)本身就是
t
t
t的函数。为了计算
f
f
f相对于
t
t
t的梯度,我们需要对多元函数使用链式法则:
d
f
d
t
=
[
∂
f
∂
x
1
∂
f
∂
x
2
]
[
∂
x
1
(
t
)
∂
t
∂
x
2
(
t
)
∂
t
]
=
∂
f
∂
x
1
∂
x
1
∂
t
+
∂
f
∂
x
2
∂
x
2
∂
t
\frac{\mathrm{d} f}{\mathrm{~d} t}=\left[\begin{array}{ll}\frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}}\end{array}\right]\left[\begin{array}{l}\frac{\partial x_{1}(t)}{\partial t} \\\frac{\partial x_{2}(t)}{\partial t}\end{array}\right]=\frac{\partial f}{\partial x_{1}} \frac{\partial x_{1}}{\partial t}+\frac{\partial f}{\partial x_{2}} \frac{\partial x_{2}}{\partial t}
dtdf=[∂x1∂f∂x2∂f][∂t∂x1(t)∂t∂x2(t)]=∂x1∂f∂t∂x1+∂x2∂f∂t∂x2
其中 d \mathrm{d} d表示梯度, ∂ ∂ ∂表示偏导数。
例 5.8
考虑
f
(
x
1
,
x
2
)
=
x
1
2
+
2
x
2
f\left(x_{1}, x_{2}\right)=x_{1}^{2}+2 x_{2}
f(x1,x2)=x12+2x2,其中
x
1
=
sin
t
x_{1}=\sin t
x1=sint,
x
2
=
cos
t
x_{2}=\cos t
x2=cost,那么:
d
f
d
t
=
∂
f
∂
x
1
∂
x
1
∂
t
+
∂
f
∂
x
2
∂
x
2
∂
t
=
2
sin
t
∂
sin
t
∂
t
+
2
∂
cos
t
∂
t
=
2
sin
t
cos
t
−
2
sin
t
=
2
sin
t
(
cos
t
−
1
)
\begin{aligned}\frac{\mathrm{d} f}{\mathrm{~d} t} &=\frac{\partial f}{\partial x_{1}} \frac{\partial x_{1}}{\partial t}+\frac{\partial f}{\partial x_{2}} \frac{\partial x_{2}}{\partial t} \\&=2 \sin t \frac{\partial \sin t}{\partial t}+2 \frac{\partial \cos t}{\partial t} \\&=2 \sin t \cos t-2 \sin t=2 \sin t(\cos t-1)\end{aligned}
dtdf=∂x1∂f∂t∂x1+∂x2∂f∂t∂x2=2sint∂t∂sint+2∂t∂cost=2sintcost−2sint=2sint(cost−1)
是
f
f
f对
t
t
t的导数。
如果
f
(
x
1
,
x
2
)
f(x_1,x_2)
f(x1,x2)是
x
1
x_1
x1和
x
2
x_2
x2的函数,其中
x
1
(
s
,
t
)
x_1(s,t)
x1(s,t)和
x
2
(
s
,
t
)
x_2(s,t)
x2(s,t)是两个变量
s
s
s和
t
t
t的函数,则用链式法则求得偏导数为:
∂
f
∂
s
=
∂
f
∂
x
1
∂
x
1
∂
s
+
∂
f
∂
x
2
∂
x
2
∂
s
\frac{\partial f}{\partial \textcolor{orange}{s}}=\frac{\partial f}{\partial \textcolor{blue}{x_{1}}} \frac{\partial \textcolor{blue}{x_{1}}}{\partial \textcolor{orange}{s}}+\frac{\partial f}{\partial \textcolor{blue}{x_{2}}} \frac{\partial \textcolor{blue}{x_{2}}}{\partial \textcolor{orange}{s}}
∂s∂f=∂x1∂f∂s∂x1+∂x2∂f∂s∂x2
∂ f ∂ t = ∂ f ∂ x 1 ∂ x 1 ∂ t + ∂ f ∂ x 2 ∂ x 2 ∂ t \frac{\partial f}{\partial \textcolor{orange}{t}}=\frac{\partial f}{\partial \textcolor{blue}{x_{1}}} \frac{\partial \textcolor{blue}{x_{1}}}{\partial \textcolor{orange}{t}}+\frac{\partial f}{\partial \textcolor{blue}{x_{2}}} \frac{\partial \textcolor{blue}{x_{2}}}{\partial \textcolor{orange}{t}} ∂t∂f=∂x1∂f∂t∂x1+∂x2∂f∂t∂x2
梯度由矩阵相乘得到
d
f
d
(
s
,
t
)
=
∂
f
∂
x
∂
x
∂
(
s
,
t
)
=
[
∂
f
∂
x
1
∂
f
∂
x
2
]
⏟
=
∂
f
∂
x
[
∂
x
1
∂
s
∂
x
1
∂
t
∂
x
2
∂
s
∂
x
2
∂
t
]
⏟
=
∂
x
∂
(
s
,
t
)
\frac{\mathrm{d} f}{\mathrm{~d}(s, t)}=\frac{\partial f}{\partial \boldsymbol{x}} \frac{\partial \boldsymbol{x}}{\partial(s, t)}=\underbrace{\left[\frac{\partial f}{\textcolor{blue}{\partial x_{1}}} \quad \frac{\partial f}{\textcolor{orange}{\partial x_{2}}}\right]}_{=\frac{\partial f}{\partial \boldsymbol{x}}} \underbrace{\left[\begin{array}{cc}\textcolor{blue}{\frac{\partial x_{1}}{\partial s}} & \textcolor{blue}{\frac{\partial x_{1}}{\partial t}} \\\textcolor{orange}{\frac{\partial x_{2}}{\partial s}} & \textcolor{orange}{\frac{\partial x_{2}}{\partial t}}\end{array}\right]}_{=\frac{\partial \boldsymbol{x}}{\partial(s, t)}}
d(s,t)df=∂x∂f∂(s,t)∂x==∂x∂f
[∂x1∂f∂x2∂f]=∂(s,t)∂x
[∂s∂x1∂s∂x2∂t∂x1∂t∂x2]
这种将链式规则写成矩阵乘法的简洁方法只有在将梯度定义为行向量时才有意义。否则,我们将需要转置矩阵来匹配维数。转置对象是向量或矩阵时,转置是小事一桩;然而,当对象是张量时(我们将在下面讨论),转置就不再是小事了。
备注:验证梯度实现的正确性
在计算机程序中对梯度的正确性进行数值检验时,可以利用偏导数的定义中差商(见5.39)的极限:当我们计算梯度并实现它们时,我们可以使用有限差分对我们的实现结果进行数值检验:我们选择一个较小值
h
h
h(例如,
h
=
1
0
−
4
h=10^{−4}
h=10−4),并将偏导数的定义中的有限差分近似值与梯度的解析结果进行比较。如果误差很小,我们的梯度实现很有可能是正确的。“小”可以是
∑
i
(
d
h
i
−
d
f
i
)
2
∑
i
(
d
h
i
+
d
f
i
)
2
<
1
0
−
6
\sqrt{\frac{\sum_{i}\left(d h_{i}-d f_{i}\right)^{2}}{\sum_{i}\left(d h_{i}+d f_{i}\right)^{2}}}<10^{-6}
∑i(dhi+dfi)2∑i(dhi−dfi)2<10−6,其中
d
h
i
dh_i
dhi是有限差分近似,
d
f
i
df_i
dfi是
f
f
f关于第
i
i
i变量
x
i
x_i
xi的解析梯度。
.
5.3 向量值函数的梯度
到目前为止,我们讨论了映射到实数的函数 f : R n → R f:\mathbb{R}^{n} \rightarrow \mathbb{R} f:Rn→R的偏导数和梯度。下面,我们将梯度的概念推广到向量值函数(向量场) f : R n → R m \boldsymbol{f}:\mathbb{R}^{n} \rightarrow \mathbb{R}^m f:Rn→Rm,其中 n ≥ 1 , m > 1 n\ge 1,m\gt 1 n≥1,m>1。
对于一个函数
f
:
R
n
→
R
m
\boldsymbol{f}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}
f:Rn→Rm,
x
=
[
x
1
,
…
,
x
n
]
⊤
∈
R
n
\boldsymbol{x}=\left[x_{1}, \ldots, x_{n}\right]^{\top} \in \mathbb{R}^{n}
x=[x1,…,xn]⊤∈Rn,相应的函数值向量如下所示:
f
(
x
)
=
[
f
1
(
x
)
⋮
f
m
(
x
)
]
∈
R
m
\boldsymbol{f}(\boldsymbol{x})=\left[\begin{array}{c}f_{1}(\boldsymbol{x}) \\\vdots \\f_{m}(\boldsymbol{x})\end{array}\right] \in \mathbb{R}^{m}
f(x)=⎣⎢⎡f1(x)⋮fm(x)⎦⎥⎤∈Rm
用这种方法写向量值函数,可以把向量值函数 f : R n → R m \boldsymbol{f}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m} f:Rn→Rm看作函数的向量 [ f 1 , … , f m ] ⊤ \left[f_{1}, \ldots, f_{m}\right]^{\top} [f1,…,fm]⊤,其中每个 f i : R n → R f_{i}: \mathbb{R}^{n} \rightarrow \mathbb{R} fi:Rn→R的微分法则正是我们在第5.2节中讨论的法则。
因此,向量值函数
f
:
R
n
→
R
m
\boldsymbol{f}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}
f:Rn→Rm关于
x
i
∈
R
,
i
=
1
,
.
.
.
,
n
x_i\in\mathbb{R},i=1,...,n
xi∈R,i=1,...,n的偏导数由以下向量给出:
∂
f
∂
x
i
=
[
∂
f
1
∂
x
i
⋮
∂
f
m
∂
x
i
]
=
[
lim
h
→
0
f
1
(
x
1
,
…
,
x
i
−
1
,
x
i
+
h
,
x
i
+
1
,
…
x
n
)
−
f
1
(
x
)
h
⋮
lim
h
→
0
f
m
(
x
1
,
…
,
x
i
−
1
,
x
i
+
h
,
x
i
+
1
,
…
x
n
)
−
f
m
(
x
)
h
]
∈
R
m
(
5.55
)
\frac{\partial \boldsymbol{f}}{\partial x_{i}}=\left[\begin{array}{c}\frac{\partial f_{1}}{\partial x_{i}} \\\vdots \\\frac{\partial f_{m}}{\partial x_{i}}\end{array}\right]=\left[\begin{array}{c}\lim _{h \rightarrow 0} \frac{f_{1}\left(x_{1}, \ldots, x_{i-1}, x_{i}+h, x_{i+1}, \ldots x_{n}\right)-f_{1}(\boldsymbol{x})}{h} \\\vdots \\\lim _{h \rightarrow 0} \frac{f_{m}\left(x_{1}, \ldots, x_{i-1}, x_{i}+h, x_{i+1}, \ldots x_{n}\right)-f_{m}(\boldsymbol{x})}{h}\end{array}\right] \in \mathbb{R}^{m}\qquad (5.55)
∂xi∂f=⎣⎢⎡∂xi∂f1⋮∂xi∂fm⎦⎥⎤=⎣⎢⎡limh→0hf1(x1,…,xi−1,xi+h,xi+1,…xn)−f1(x)⋮limh→0hfm(x1,…,xi−1,xi+h,xi+1,…xn)−fm(x)⎦⎥⎤∈Rm(5.55)
由(5.40)可知,非向量
f
f
f相对于向量的梯度是偏导数组成的行向量。在(5.55)中,每一个偏导数
∂
f
/
∂
x
i
∂\boldsymbol{f}/∂x_i
∂f/∂xi则是一个列向量。因此,我们通过组合这些偏导数得到
f
:
R
n
→
R
m
\boldsymbol{f}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}
f:Rn→Rm相对于
x
∈
R
n
\boldsymbol{x} \in \mathbb{R}^{n}
x∈Rn的梯度:

定义 5.6 雅可比矩阵
向量值函数
f
:
R
n
→
R
m
\boldsymbol{f}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}
f:Rn→Rm的所有一阶偏导数的集合称为雅可比矩阵(Jacobian)。雅可比矩阵
J
\boldsymbol{J}
J是一个
m
×
n
m×n
m×n矩阵,我们将其定义和排列如下:
J
=
∇
x
f
=
d
f
(
x
)
d
x
=
[
∂
f
(
x
)
∂
x
1
⋯
∂
f
(
x
)
∂
x
n
]
\boldsymbol{J}=\nabla_{\boldsymbol{x}} \boldsymbol{f}=\frac{\mathrm{d} \boldsymbol{f}(\boldsymbol{x})}{\mathrm{d} \boldsymbol{x}}=\left[\begin{array}{lll}\frac{\partial \boldsymbol{f}(\boldsymbol{x})}{\partial x_{1}} & \cdots & \frac{\partial \boldsymbol{f}(\boldsymbol{x})}{\partial x_{n}}\end{array}\right]
J=∇xf=dxdf(x)=[∂x1∂f(x)⋯∂xn∂f(x)]
=
[
∂
f
1
(
x
)
∂
x
1
⋯
∂
f
1
(
x
)
∂
x
n
⋮
⋮
∂
f
m
(
x
)
∂
x
1
⋯
∂
f
m
(
x
)
∂
x
n
]
(
5.58
)
=\left[\begin{array}{ccc}\frac{\partial f_{1}(\boldsymbol{x})}{\partial x_{1}} & \cdots & \frac{\partial f_{1}(\boldsymbol{x})}{\partial x_{n}} \\\vdots & & \vdots \\\frac{\partial f_{m}(\boldsymbol{x})}{\partial x_{1}} & \cdots & \frac{\partial f_{m}(\boldsymbol{x})}{\partial x_{n}}\end{array}\right]\qquad(5.58)
=⎣⎢⎢⎡∂x1∂f1(x)⋮∂x1∂fm(x)⋯⋯∂xn∂f1(x)⋮∂xn∂fm(x)⎦⎥⎥⎤(5.58)
x = [ x 1 ⋮ x n ] , J ( i , j ) = ∂ f i ∂ x j \boldsymbol{x}=\left[\begin{array}{c}x_{1} \\\vdots \\x_{n}\end{array}\right], \quad J(i, j)=\frac{\partial f_{i}}{\partial x_{j}} x=⎣⎢⎡x1⋮xn⎦⎥⎤,J(i,j)=∂xj∂fi
作为(5.58)的一个特例,函数 f : R n → R 1 f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{1} f:Rn→R1将向量 x ∈ R n \boldsymbol{x} \in \mathbb{R}^{n} x∈Rn映射到标量(例如 f ( x ) = ∑ i = 1 n x i f(\boldsymbol{x})=\sum_{i=1}^{n} x_{i} f(x)=∑i=1nxi),其对应的雅可比矩阵是一个行向量(维数 1 × n 1×n 1×n的矩阵);参见公式(5.40)。
备注:
在这本书中,我们使用了导数的分子布局(numerator layout),即
f
∈
R
m
\boldsymbol{f} \in \mathbb{R}^{m}
f∈Rm对
x
∈
R
n
\boldsymbol{x} \in \mathbb{R}^{n}
x∈Rn的导数
d
f
/
d
x
\mathrm{d} \boldsymbol{f} / \mathrm{d} \boldsymbol{x}
df/dx是一个
m
×
n
m×n
m×n矩阵,其中
f
\boldsymbol{f}
f的元素定义了相应雅可比矩阵的行,
x
\boldsymbol{x}
x的元素定义了相应雅可比矩阵的列;见(5.58)。还有分母布局(denominator layout),它是分子布局的转置。
我们将在第6.7节中看到雅可比矩阵如何用于概率分布的变量变换方法。由于变量变换而产生的缩放量可由行列式得到。

图 5.5
f
\boldsymbol{f}
f的雅可比矩阵的行列式可以用来计算蓝色和橙色区域之间的放大倍数。
在第4.1节中,我们看到行列式可以用来计算平行四边形的面积。如果给定两个向量
b
1
=
[
1
,
0
]
⊤
,
b
2
=
[
0
,
1
]
⊤
\boldsymbol{b}_{1}=[1,0]^{\top},\boldsymbol{b}_{2}=[0,1]^{\top}
b1=[1,0]⊤,b2=[0,1]⊤作为单位正方形(图5.5中的蓝色区域)的边,则该正方形的面积为:
∣
det
(
[
1
0
0
1
]
)
∣
=
1
\left|\operatorname{det}\left(\left[\begin{array}{ll}1 & 0 \\0 & 1\end{array}\right]\right)\right|=1
∣∣∣∣det([1001])∣∣∣∣=1
如果我们取一个平行四边形(图5.5中的橙色区域),它的边为
c
1
=
[
−
2
,
1
]
⊤
,
c
2
=
[
1
,
1
]
⊤
\boldsymbol{c}_{1}=[-2,1]^{\top}, \boldsymbol{c}_{2}=[1,1]^{\top}
c1=[−2,1]⊤,c2=[1,1]⊤,则它的面积是行列式(见第4.1节)的绝对值
∣
det
(
[
−
2
1
1
1
]
)
∣
=
∣
−
3
∣
=
3
\left|\operatorname{det}\left(\left[\begin{array}{cc}-2 & 1 \\1 & 1\end{array}\right]\right)\right|=|-3|=3
∣∣∣∣det([−2111])∣∣∣∣=∣−3∣=3
即它的面积正好是单位方形的三倍。我们可以通过一个将单位方形转换成另一个方形的映射来找到这个缩放因子。用线性代数的术语说,就是有效地执行从 ( b 1 , b 2 ) \left(\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\right) (b1,b2)到 ( c 1 , c 2 ) \left(\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\right) (c1,c2)的变量变换。在我们的例子中,这个映射是线性的,且它的行列式的绝对值正好给出了我们要寻找的缩放因子。
我们将描述两种确定这种映射的方法。首先,我们假设映射是线性的,这样我们就可以使用第2章中的工具来确定这个映射。其次,我们将使用我们在本章中讨论的工具,找到使用偏导数的映射。
方法 1
为了开始使用线性代数的方法,我们首先确定
{
b
1
,
b
2
}
\left\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\right\}
{b1,b2}和
{
c
1
,
c
2
}
\left\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\right\}
{c1,c2}都是
R
2
\mathbb{R}^2
R2的基。我们要有效地执行的是从
{
b
1
,
b
2
}
\left\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\right\}
{b1,b2}到
{
c
1
,
c
2
}
\left\{\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\right\}
{c1,c2}的基变换,就得寻找实现基变换的变换矩阵。利用第2.7.2节的结果,我们确定了所需的基变化矩阵为
J
=
[
−
2
1
1
1
]
(
5.62
)
\boldsymbol{J}=\left[\begin{array}{cc}-2 & 1 \\1 & 1\end{array}\right]\qquad (5.62)
J=[−2111](5.62)
它使得
J
b
1
=
c
1
\boldsymbol{J}\boldsymbol{b}_1=\boldsymbol{c}_1
Jb1=c1,
J
b
2
=
c
2
\boldsymbol{J}\boldsymbol{b}_2=\boldsymbol{c}_2
Jb2=c2。
J
\boldsymbol{J}
J的行列式的绝对值
∣
det
(
J
)
∣
=
3
|\operatorname{det}(\boldsymbol{J})|=3
∣det(J)∣=3,这正是我们在寻找的缩放因子,即
(
c
1
,
c
2
)
\left(\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\right)
(c1,c2)所张成的四边形的面积是
(
b
1
,
b
2
)
\left(\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\right)
(b1,b2)所张成的面积的三倍。
方法 2
线性代数方法适用于线性变换;对于非线性变换(与第6.7节有关),我们有基于偏微分的更一般的方法。
在这种方法中,我们考虑执行变量变换的函数
f
:
R
2
→
R
2
\boldsymbol{f}: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}
f:R2→R2。在我们的例子中,
f
\boldsymbol{f}
f将关于
(
b
1
,
b
2
)
\left(\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\right)
(b1,b2)的任意向量
x
∈
R
2
\boldsymbol{x} \in \mathbb{R}^{2}
x∈R2的坐标映射到关于
(
c
1
,
c
2
)
\left(\boldsymbol{c}_{1}, \boldsymbol{c}_{2}\right)
(c1,c2)的坐标
y
∈
R
2
\boldsymbol{y} \in \mathbb{R}^{2}
y∈R2。我们想确定映射,这样我们就可以计算出一个面积(或体积)被
f
\boldsymbol{f}
f变换时它是如何变化的。为此,我们需要找出
f
(
x
)
\boldsymbol{f}(\boldsymbol{x})
f(x)在
x
\boldsymbol{x}
x微小变化时它是如何变化的。雅可比矩阵
d
f
d
x
∈
R
2
×
2
\frac{\mathrm{d} \boldsymbol{f}}{\mathrm{d} \boldsymbol{x}} \in \mathbb{R}^{2 \times 2}
dxdf∈R2×2正是这个问题的答案。由
y
1
=
−
2
x
1
+
x
2
y_{1}=-2 x_{1}+x_{2}
y1=−2x1+x2
y
2
=
x
1
+
x
2
y_{2}=x_{1}+x_{2}
y2=x1+x2
我们得到了
x
\boldsymbol{x}
x和
y
\boldsymbol{y}
y之间的函数关系,这允许我们计算得到偏导数
∂
y
1
∂
x
1
=
−
2
,
∂
y
1
∂
x
2
=
1
,
∂
y
2
∂
x
1
=
1
,
∂
y
2
∂
x
2
=
1
\frac{\partial y_{1}}{\partial x_{1}}=-2, \quad \frac{\partial y_{1}}{\partial x_{2}}=1, \quad \frac{\partial y_{2}}{\partial x_{1}}=1, \quad \frac{\partial y_{2}}{\partial x_{2}}=1
∂x1∂y1=−2,∂x2∂y1=1,∂x1∂y2=1,∂x2∂y2=1
将它们组合成雅可比矩阵:
J
=
[
∂
y
1
∂
x
1
∂
y
1
∂
x
2
∂
y
2
∂
x
1
∂
y
2
∂
x
2
]
=
[
−
2
1
1
1
]
(
5.66
)
\boldsymbol{J}=\left[\begin{array}{ll}\frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} \\\frac{\partial y_{2}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{2}}\end{array}\right]=\left[\begin{array}{cc}-2 & 1 \\1 & 1\end{array}\right]\qquad (5.66)
J=[∂x1∂y1∂x1∂y2∂x2∂y1∂x2∂y2]=[−2111](5.66)
雅可比矩阵表示我们想要的坐标变换。如果坐标变换是线性的(如我们的例子),那么它是精确的,(5.66)精确地恢复了(5.62)中的基变化矩阵。如果坐标变换是非线性的,雅可比矩阵则用一个线性变换局部地逼近这个非线性变换。雅可比行列式 ∣ det ( J ) ∣ |\operatorname{det}(\boldsymbol{J})| ∣det(J)∣的绝对值是变换坐标时面积或体积的缩放因子。我们的例子得到 ∣ det ( J ) ∣ = 3 |\operatorname{det}(\boldsymbol{J})|=3 ∣det(J)∣=3。
当我们在第6.7节变换随机变量和概率分布时,将使用到雅可比行列式和变量变换。在机器学习中,这些变换与使用重参数化技巧(reparametrization trick)(也称为infinite perturbation analysis)训练深度神经网络关系密切。
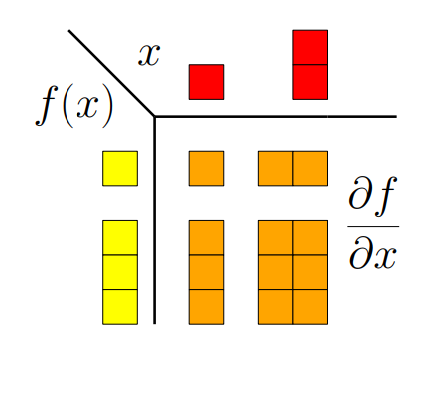
图 5.6(偏)导数的维度。
在这一章中,我们学习了函数的导数。图5.6总结了变量-函数在各种情况下导数的维度。如果 f : R → R f: \mathbb{R} \rightarrow \mathbb{R} f:R→R,梯度就是一个标量(左上角的那一块)。对于 f : R D → R f: \mathbb{R}^{D} \rightarrow \mathbb{R} f:RD→R,梯度是 1 × D 1×D 1×D的行向量(右上角那一块)。对于 f : R → R E \boldsymbol{f}: \mathbb{R} \rightarrow \mathbb{R}^{E} f:R→RE,梯度是 E × 1 E×1 E×1列向量(左下角的那一块),对于 f : R D → R E \boldsymbol{f}: \mathbb{R}^{D} \rightarrow \mathbb{R}^{E} f:RD→RE,梯度是 E × D E×D E×D矩阵(右下角那一块)。
例 5.9 向量值函数的梯度
给定 f ( x ) = A x , f ( x ) ∈ R M , A ∈ R M × N , x ∈ R N \boldsymbol{f}(\boldsymbol{x})=\boldsymbol{A} \boldsymbol{x}, \quad \boldsymbol{f}(\boldsymbol{x}) \in \mathbb{R}^{M}, \quad \boldsymbol{A} \in \mathbb{R}^{M \times N}, \quad \boldsymbol{x} \in \mathbb{R}^{N} f(x)=Ax,f(x)∈RM,A∈RM×N,x∈RN
为了计算梯度
d
f
/
d
x
\mathrm{d} \boldsymbol{f} / \mathrm{d} \boldsymbol{x}
df/dx,我们首先确定
d
f
/
d
x
\mathrm{d} \boldsymbol{f} / \mathrm{d} \boldsymbol{x}
df/dx的维数:由于
f
:
R
N
→
R
M
\boldsymbol{f}: \mathbb{R}^{N} \rightarrow \mathbb{R}^{M}
f:RN→RM,因此
d
f
/
d
x
∈
R
M
×
N
\mathrm{d} \boldsymbol{f} / \mathrm{d} \boldsymbol{x} \in \mathbb{R}^{M \times N}
df/dx∈RM×N。其次,为了计算梯度,我们还需要确定
f
f
f对每个
x
j
x_j
xj的偏导数:
f
i
(
x
)
=
∑
j
=
1
N
A
i
j
x
j
⟹
∂
f
i
∂
x
j
=
A
i
j
f_{i}(\boldsymbol{x})=\sum_{j=1}^{N} A_{i j} x_{j} \Longrightarrow \frac{\partial f_{i}}{\partial x_{j}}=A_{i j}
fi(x)=j=1∑NAijxj⟹∂xj∂fi=Aij
我们收集雅可比矩阵中的偏导数,得到梯度
d
f
d
x
=
[
∂
f
1
∂
x
1
⋯
∂
f
1
∂
x
N
⋮
⋮
∂
f
M
∂
x
1
⋯
∂
f
M
∂
x
N
]
=
[
A
11
⋯
A
1
N
⋮
⋮
A
M
1
⋯
A
M
N
]
=
A
∈
R
M
×
N
\frac{\mathrm{d} \boldsymbol{f}}{\mathrm{d} \boldsymbol{x}}=\left[\begin{array}{ccc}\frac{\partial f_{1}}{\partial x_{1}} & \cdots & \frac{\partial f_{1}}{\partial x_{N}} \\\vdots & & \vdots \\\frac{\partial f_{M}}{\partial x_{1}} & \cdots & \frac{\partial f_{M}}{\partial x_{N}}\end{array}\right]=\left[\begin{array}{ccc}A_{11} & \cdots & A_{1 N} \\\vdots & & \vdots \\A_{M 1} & \cdots & A_{M N}\end{array}\right]=\boldsymbol{A} \in \mathbb{R}^{M \times N}
dxdf=⎣⎢⎡∂x1∂f1⋮∂x1∂fM⋯⋯∂xN∂f1⋮∂xN∂fM⎦⎥⎤=⎣⎢⎡A11⋮AM1⋯⋯A1N⋮AMN⎦⎥⎤=A∈RM×N
例 5.10链式法则
考虑函数
h
:
R
→
R
,
h
(
t
)
=
(
f
∘
g
)
(
t
)
h: \mathbb{R} \rightarrow \mathbb{R}, h(t)=(f \circ g)(t)
h:R→R,h(t)=(f∘g)(t),其中
f
:
R
2
→
R
f: \mathbb{R}^{2} \rightarrow \mathbb{R}
f:R2→R
g
:
R
→
R
2
g: \mathbb{R} \rightarrow \mathbb{R}^{2}
g:R→R2
f
(
x
)
=
exp
(
x
1
x
2
2
)
f(\boldsymbol{x})=\exp \left(x_{1} x_{2}^{2}\right)
f(x)=exp(x1x22)
x
=
[
x
1
x
2
]
=
g
(
t
)
=
[
t
cos
t
t
sin
t
]
(
5.72
)
\boldsymbol{x}=\left[\begin{array}{l}x_{1} \\x_{2}\end{array}\right]=g(t)=\left[\begin{array}{l}t \cos t \\t \sin t\end{array}\right] \qquad (5.72)
x=[x1x2]=g(t)=[tcosttsint](5.72)
计算
h
h
h关于
t
t
t的梯度。由
f
:
R
2
→
R
f: \mathbb{R}^{2} \rightarrow \mathbb{R}
f:R2→R和
g
:
R
→
R
2
g: \mathbb{R} \rightarrow \mathbb{R}^{2}
g:R→R2,我们注意到
∂
f
∂
x
∈
R
1
×
2
,
∂
g
∂
t
∈
R
2
×
1
\frac{\partial f}{\partial \boldsymbol{x}} \in \mathbb{R}^{1 \times 2}, \quad \frac{\partial g}{\partial t} \in \mathbb{R}^{2 \times 1}
∂x∂f∈R1×2,∂t∂g∈R2×1
通过应用链式法则计算所需的梯度:
d
h
d
t
=
∂
f
∂
x
∂
x
∂
t
=
[
∂
f
∂
x
1
∂
f
∂
x
2
]
[
∂
x
1
∂
t
∂
x
2
∂
t
]
=
[
exp
(
x
1
x
2
2
)
x
2
2
2
exp
(
x
1
x
2
2
)
x
1
x
2
]
[
cos
t
−
t
sin
t
sin
t
+
t
cos
t
]
=
exp
(
x
1
x
2
2
)
(
x
2
2
(
cos
t
−
t
sin
t
)
+
2
x
1
x
2
(
sin
t
+
t
cos
t
)
)
\begin{aligned}\frac{\mathrm{d} h}{\mathrm{~d} t} &=\textcolor{blue}{\frac{\partial f}{\partial x}} \textcolor{orange}{\frac{\partial x}{\partial t}}=\textcolor{blue}{\left[\begin{array}{ll}\frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}}\end{array}\right]}\textcolor{orange}{\left[\frac{\frac{\partial x_{1}}{\partial t}}{\frac{\partial x_{2}}{\partial t}}\right]} \\&=\textcolor{blue}{\left[\exp \left(x_{1} x_{2}^{2}\right) x_{2}^{2} \quad 2 \exp \left(x_{1} x_{2}^{2}\right) x_{1} x_{2}\right]}\textcolor{orange}{\left[\begin{array}{c}\cos t-t \sin t \\\sin t+t \cos t\end{array}\right]} \\&=\exp \left(x_{1} x_{2}^{2}\right)\left(x_{2}^{2}(\cos t-t \sin t)+2 x_{1} x_{2}(\sin t+t \cos t)\right)\end{aligned}
dtdh=∂x∂f∂t∂x=[∂x1∂f∂x2∂f][∂t∂x2∂t∂x1]=[exp(x1x22)x222exp(x1x22)x1x2][cost−tsintsint+tcost]=exp(x1x22)(x22(cost−tsint)+2x1x2(sint+tcost))
其中 x 1 = t cos t , x 2 = t sin t x_{1}=t \cos t,x_{2}=t \sin t x1=tcost,x2=tsint,见(5.72)。
例 5.11 线性模型中最小二乘损失的梯度
考虑线性模型
y
=
Φ
θ
\boldsymbol{y}=\boldsymbol{\Phi} \boldsymbol{\theta}
y=Φθ
其中
θ
∈
R
D
\boldsymbol{\theta} \in \mathbb{R}^{D}
θ∈RD是参数向量,
Φ
∈
R
N
×
D
\mathbf{\Phi} \in \mathbb{R}^{N \times D}
Φ∈RN×D为输入的特征值而
y
∈
R
N
\boldsymbol{y} \in \mathbb{R}^{N}
y∈RN为响应值。我们定义函数:
L
(
e
)
:
=
∥
e
∥
2
L(\boldsymbol{e}):=\|\boldsymbol{e}\|^{2}
L(e):=∥e∥2
e
(
θ
)
:
=
y
−
Φ
θ
(
5.77
)
\boldsymbol{e}(\boldsymbol{\theta}):=\boldsymbol{y}-\boldsymbol{\Phi} \boldsymbol{\theta}\qquad (5.77)
e(θ):=y−Φθ(5.77)
并使用链式法则求
∂
L
∂
θ
\frac{\partial L}{\partial \boldsymbol{\theta}}
∂θ∂L。
L
L
L被称为最小二乘损失(least-squares loss)函数。
在开始计算之前,我们确定梯度的维数为
∂
L
∂
θ
∈
R
1
×
D
\frac{\partial L}{\partial \boldsymbol{\theta}} \in \mathbb{R}^{1 \times D}
∂θ∂L∈R1×D
链式法则允许我们计算梯度
∂
L
∂
θ
=
∂
L
∂
e
∂
e
∂
θ
\frac{\partial L}{\partial \boldsymbol{\theta}}=\textcolor{blue}{\frac{\partial L}{\partial \boldsymbol{e}}}\textcolor{orange}{ \frac{\partial \boldsymbol{e}}{\partial \boldsymbol{\theta}}}
∂θ∂L=∂e∂L∂θ∂e
其中第
d
d
d个元素由以下得到:
∂
L
∂
θ
[
1
,
d
]
=
∑
n
=
1
N
∂
L
∂
e
[
n
]
∂
e
∂
θ
[
n
,
d
]
\frac{\partial L}{\partial \boldsymbol{\theta}}[1, d]=\sum_{n=1}^{N} \frac{\partial L}{\partial \boldsymbol{e}}[n] \frac{\partial \boldsymbol{e}}{\partial \boldsymbol{\theta}}[n, d]
∂θ∂L[1,d]=n=1∑N∂e∂L[n]∂θ∂e[n,d]
我们知道
∥
e
∥
2
=
e
⊤
e
\|\boldsymbol{e}\|^{2}=\boldsymbol{e}^{\top} \boldsymbol{e}
∥e∥2=e⊤e(见第3.2节),并确定
∂
L
∂
e
=
2
e
⊤
∈
R
1
×
N
\textcolor{blue}{\frac{\partial L}{\partial e}=2 e^{\top}} \in \mathbb{R}^{1 \times N}
∂e∂L=2e⊤∈R1×N
此外,我们得到
∂
e
∂
θ
=
−
Φ
∈
R
N
×
D
\textcolor{orange}{\frac{\partial e}{\partial \theta}=-\Phi} \in \mathbb{R}^{N \times D}
∂θ∂e=−Φ∈RN×D
最后得到我们的期望导数为:
∂
L
∂
θ
=
−
2
e
⊤
Φ
=
(
5.77
)
−
2
(
y
⊤
−
θ
⊤
Φ
⊤
)
⏟
1
×
N
Φ
⏟
N
×
D
∈
R
1
×
D
\frac{\partial L}{\partial \boldsymbol{\theta}}=\textcolor{orange}{-}\textcolor{blue}{2 \boldsymbol{e}^{\top}} \textcolor{orange}{\boldsymbol{\Phi}} \stackrel{(5.77)}{=}\textcolor{orange}{-}\textcolor{blue}{\underbrace{2\left(\boldsymbol{y}^{\top}-\boldsymbol{\theta}^{\top} \boldsymbol{\Phi}^{\top}\right)}_{1 \times N}}\textcolor{orange}{ \underbrace{\mathbf{\Phi}}_{N \times D}} \in \mathbb{R}^{1 \times D}
∂θ∂L=−2e⊤Φ=(5.77)−1×N
2(y⊤−θ⊤Φ⊤)N×D
Φ∈R1×D
备注:如果不使用链式法则,而是通过对以下函数求导:
L
2
(
θ
)
:
=
∥
y
−
Φ
θ
∥
2
=
(
y
−
Φ
θ
)
⊤
(
y
−
Φ
θ
)
L_{2}(\boldsymbol{\theta}):=\|\boldsymbol{y}-\boldsymbol{\Phi} \boldsymbol{\theta}\|^{2}=(\boldsymbol{y}-\boldsymbol{\Phi} \boldsymbol{\theta})^{\top}(\boldsymbol{y}-\boldsymbol{\Phi} \boldsymbol{\theta})
L2(θ):=∥y−Φθ∥2=(y−Φθ)⊤(y−Φθ)
我们也可以得到相同的结果,。这种方法对于像
L
2
L_2
L2这样的简单函数是可行的,但是对于复杂的函数组合却变得不切实际。
翻译自:
《MATHEMATICS FOR MACHINE LEARNING》作者是 Marc Peter Deisenroth,A Aldo Faisal 和 Cheng Soon Ong
公众号后台回复【m4ml】即可获取这本书。

























 2491
2491

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










