前些天发现一个通俗易懂,风趣幽默的人工智能学习网站:
传送门

https://arxiv.org/abs/1611.01704
文章目录
End-to-end Optimized Image Compression
这篇论文基于非线性变换提出了一个端到端优化的图像压缩框架。
一般非线性变换编码框架

工作流程如下:
(1) 通过参数为 ϕ \boldsymbol{\phi} ϕ的可微函数(analysis 变换) g a ( ⋅ ) g_a(\cdot) ga(⋅)将图像向量 x ∈ R N \boldsymbol{x}\in \mathbb{R}^N x∈RN变换到潜在码空间(latent code space)得到码域向量 y = g a ( x , ϕ ) \boldsymbol{y}=g_a(\boldsymbol{x},\boldsymbol{\phi}) y=ga(x,ϕ)。
(2) 对变换后的 y \boldsymbol{y} y进行量化,得到待压缩的离散值向量 q ∈ R N \boldsymbol{q}\in \mathbb{R}^N q∈RN。编码的码率(rate) R R R将以量化向量 q \boldsymbol{q} q的离散概率分布 P q P_q Pq的熵 H [ P q ] H[P_q] H[Pq]作为下界。
(3) 为了重建压缩图像,将 q \boldsymbol{q} q的离散元素重新解释(reinterpreted)为连续值向量 y ^ \hat{\boldsymbol{y}} y^。然后通过参数为 θ \boldsymbol{\theta} θ的可微函数(synthesis变换) g s ( ⋅ ) g_s(\cdot) gs(⋅)将 y ^ \hat{\boldsymbol{y}} y^变换回数据域(data space)得到重建图像 x ^ = g s ( y ^ , θ ) \hat{\boldsymbol{x}}=g_s(\hat{\boldsymbol{y}},\boldsymbol{\theta}) x^=gs(y^,θ)
(4) 失真(distortion) D D D通过使用(固定)变换 z = g p ( x ) \boldsymbol{z}=g_p(\boldsymbol{x}) z=gp(x)和 z ^ = g p ( x ^ ) \hat{\boldsymbol{z}}=g_p(\hat{\boldsymbol{x}}) z^=gp(x^)变换到感知空间(perceptual space),并用评估度量 d ( z , z ^ ) d(\boldsymbol{z},\hat{\boldsymbol{z}}) d(z,z^)来评估失真。
(5) 一组图像上rate和distortion度量的加权和 D + λ R D+\lambda R D+λR将用于优化参数向量 φ \boldsymbol{φ} φ和 θ \boldsymbol{θ} θ,其中 λ λ λ为率的权重。
端到端优化的非线性变换编码
分析变换

分析变换 g a g_a ga有三个阶段,每个阶段由卷积、下采样和Generalized divisive normalization (GDN)(https://arxiv.org/abs/1511.06281v4)组成。将第 k k k阶段在空间位置 ( m , n ) (m, n) (m,n)的第 i i i个输入通道表示为 u i ( k ) ( m , n ) u^{(k)}_i(m, n) ui(k)(m,n),则输入图像向量 x \boldsymbol{x} x对应于 u i ( 0 ) ( m , n ) u^{(0)}_i(m, n) ui(0)(m,n);输出向量 y \boldsymbol{y} y对应于 u i ( 3 ) ( m , n ) u^{(3)}_i(m, n) ui(3)(m,n)。
每一阶段都以仿射卷积开始:
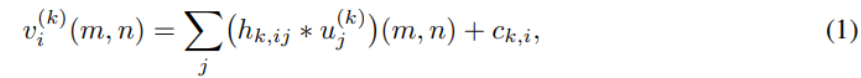
其中 ∗ * ∗表示卷积,随后是下采样:

其中 s k s_k sk为第 k k k阶段的下采样因子。
最后是GDN操作:

h 、 c 、 β h、c、β h、c、β和 γ γ γ参数构成待优化的参数向量 φ \boldsymbol{φ} φ。
合成变换

类似地,合成变换 g s g_s gs有三个阶段,每个阶段由IGDN、上采样和卷积组成。设 u ^ i ( k ) ( m , n ) \hat{u}^{(k)}_i(m, n) u^i(k)(m,n)为第 k k k个合成阶段的输入,则 y ^ \hat{\boldsymbol{y}} y^对应于 u ^ i ( 0 ) ( m , n ) \hat{u}^{(0)}_i(m, n) u^i(0)(m,n); x ^ \hat{\boldsymbol{x}} x^对应于 u ^ i ( 3 ) ( m , n ) \hat{u}^{(3)}_i(m, n) u^i(3)(m,n)。
首先,是逆GDN(IGDN)操作:

然后是上采样:

其中
s
^
k
\hat{s}_k
s^k为第
k
k
k阶段的下采样因子。
最后是仿射卷积:

参数 h ^ 、 c ^ 、 β ^ \hat{h}、\hat{c}、\hat{β} h^、c^、β^和 γ ^ \hat{γ} γ^构成待优化的参数向量 θ \boldsymbol{\theta} θ。
注意,下采样/上采样操作可以与其相邻的卷积一起实现,从而提高计算效率
感知变换
https://arxiv.org/abs/1607.05006使用Normalized Laplacian pyramid (NLP)进行变换。这里仅使用恒等变换,并使用MSE作为度量,即 d ( z , z ^ ) = ∥ z − z ^ ∥ 2 2 d(\boldsymbol{z}, \hat{\boldsymbol{z}})=\|\boldsymbol{z}-\hat{\boldsymbol{z}}\|_{2}^{2} d(z,z^)=∥z−z^∥22
非线性变换编码模型的优化
直接在图像空间中进行最优量化由于高维性而难以实现,因此作者将图像变换到码空间再用均匀标量量化器量化。通过设计合适的熵编码可以使得实际码率仅略大于量化向量的熵,因此,作者直接用熵定义目标函数:

其中两个期望将通过训练集上的多个图像的平均值来近似。
使用均匀标量量化器进行量化:

round:随机变量四舍五入,一个连续区间(区间大小为1)的随机变量值对应一个整数。
y ^ \boldsymbol{\hat{y}} y^的边缘概率密度 p y ^ i p_{\hat{y}_i} py^i由一系列Dirac delta函数(冲激函数)表示,权重等于 q i q_i qi各个区间内的概率质量函数(如图2):


【图2为 y i y_i yi(码空间元素)、 y ^ i \hat{y}_i y^i(量化元素)和 y ~ i \tilde{y}_i y~i(受均匀噪声干扰的元素)密度关系的一维图示。 p y ^ i p_{\hat{y}_i} py^i中的每个离散概率等于对应量化bin内密度 p y i p_{y_i} pyi的概率质量(由阴影表示)。密度 p y ~ i p_{\tilde{y}_i} py~i提供了一个连续函数,在整数位置与 p y ^ i p_{\hat{y}_i} py^i的离散概率值相等。】
均匀标量量化器(uniform scalar quantizer)是一个分段常数函数;其导数是不连续的(具体而言,它处处为零或无限),使得梯度下降无效。为了允许通过随机梯度下降进行优化,作者将量化器替换为附加量 ∆ y ∼ U ( 0 , 1 ) ∆\boldsymbol{y}\sim\mathcal{U}(0,1) ∆y∼U(0,1)( U \mathcal{U} U:均匀分布,0为中心,1为范围)。
替换的可行性:
首先,随机变量 y ~ = y + ∆ y \boldsymbol{\tilde{y}}=\boldsymbol{y}+∆\boldsymbol{y} y~=y+∆y,则根据Z=X+Y的分布, y ~ \boldsymbol{\tilde{y}} y~的密度函数:
p y ~ = p y ∗ U ( 0 , 1 ) p_{\boldsymbol{\tilde{y}}}=p_{\boldsymbol{y}}*\mathcal{U}(0,1) py~=py∗U(0,1)
在所有整数位置与 q \boldsymbol{q} q的概率质量函数 P q i P_{q_i} Pqi相同:

是 q \boldsymbol{q} q概率质量函数的连续松弛(图2)。这意味着 y ~ \boldsymbol{\tilde{y}} y~的微分(连续)熵 h [ p y ~ i ] h[p_{\tilde{y}_i}] h[py~i]可以用作 q \boldsymbol{q} q的熵 H [ P q i ] H[P_{q_i}] H[Pqi]的近似值。
为了减少模型误差,作者假设 y ~ \boldsymbol{\tilde{y}} y~的松弛概率模型和熵编码的码空间中的边缘独立【例如: p y ~ ( y ~ ) = ∏ i p y ~ i ( y ~ i ) p_{\tilde{\boldsymbol{y}}}(\tilde{\boldsymbol{y}})=\prod_{i} p_{\tilde{y}_{i}}\left(\tilde{y}_{i}\right) py~(y~)=∏ipy~i(y~i)( log ( ∏ i p y ~ i ( y ~ i ) ) = ∑ i log ( p y ~ i ( y ~ i ) ) \log(\prod_{i} p_{\tilde{y}_{i}}\left(\tilde{y}_{i}\right))=\sum_i\log(p_{\tilde{y}_{i}}\left(\tilde{y}_{i}\right)) log(∏ipy~i(y~i))=∑ilog(py~i(y~i))】,并对边缘 p y ~ i p_{\boldsymbol{\tilde{y}_i}} py~i进行非参数建模。具体而言,作者使用精细采样的分段线性函数,并将其更新为一维直方图。更具体地,作者使用每单位间隔10个采样点,将每个边缘 p y ~ i p_{\boldsymbol{\tilde{y}_i}} py~i表示为分段线性函数(即线性样条)。参数向量 ψ ( i ) \boldsymbol{\psi}^{(i)} ψ(i)由这些采样点处的 p y ~ i p_{\boldsymbol{\tilde{y}_i}} py~i值组成。使用普通随机梯度下降来最大化期望似然:

并在每个步骤之后重新归一化边缘密度。在每
1
0
6
10^6
106个梯度步骤之后,作者使用启发式方法调整样条近似的范围,以覆盖在训练集上获得的
y
~
\tilde{y}
y~值的范围。
第二,独立均匀噪声经用于近似量化误差(https://ieeexplore.ieee.org/document/720541)。因此,我们可以使用均匀噪声近似量化的失真。
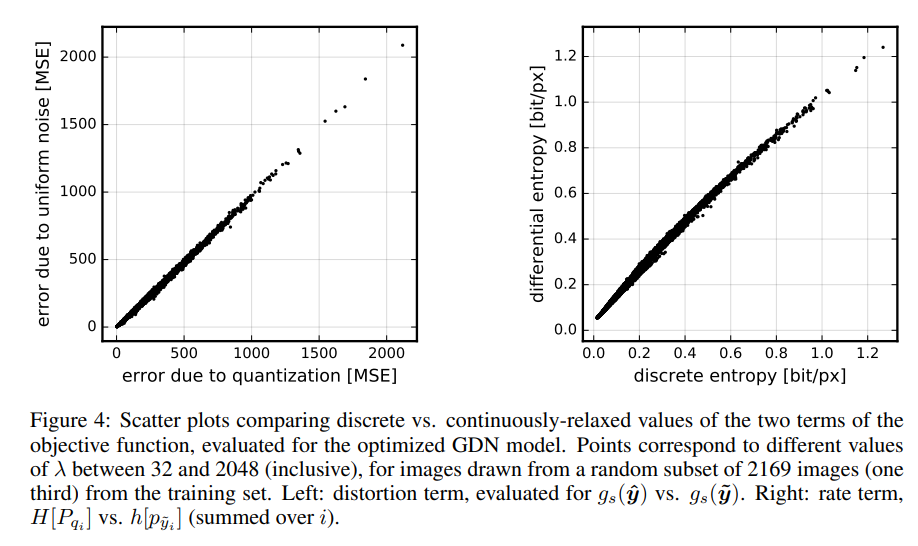
图4验证了连续松弛为实际量化的率失真值提供了良好的近似值。左图的松弛失真项大部分是无偏的,并且表现出相对较小的方差。松弛熵为较粗(coarser)量化区域的离散熵提供了某种程度的正偏估计,但如预期的那样,对于较精细(finer )量化,偏差消失。
给定量化向量 y ^ \boldsymbol{\hat{y}} y^分布的连续近似 y ~ \boldsymbol{\tilde{y}} y~,参数 θ \boldsymbol{\theta} θ 和 ϕ \boldsymbol{\phi} ϕ的损失函数可以写成:

其中,向量
ψ
(
i
)
\boldsymbol{ψ}^{(i)}
ψ(i)参数化
p
y
~
i
p_{\tilde{y}_i}
py~i的分段线性近似(与
θ
\boldsymbol{\theta}
θ 和
ϕ
\boldsymbol{\phi}
ϕ联合训练)。这是连续和可微的,因此非常适合于随机优化。
与变分生成图像模型的关系
上面从经典的率失真优化问题导出了端到端压缩的优化公式。除此之外,还可以在变分自编码器(VAE)的背景下进行推导。
在贝叶斯变分推理中,给定随机变量 x x x的观测样本集合以及生成模型 p x ∣ y ( x ∣ y ) p_{x|y}(x| y) px∣y(x∣y)。我们试图找到一个后验 p y ∣ x ( y ∣ x ) p_{y|x}(y | x) py∣x(y∣x)(通常不能用封闭形式表示)。VAE通过最小化 q ( y ∣ x ) q(y|x) q(y∣x)和 p y ∣ x ( y ∣ x ) p_{y|x}(y | x) py∣x(y∣x)之间的KL散度,用密度 q ( y ∣ x ) q(y|x) q(y∣x)近似该后验:


【图3。空心节点表示随机变量;灰色节点表示观测数据;小的黑色节点表示参数;箭头表示依赖关系。框内的节点是按图像计算的。】
如果我们定义生成模型(图3左,高斯分布以 g s g_s gs生成结果为均值)如下:

注: 对于一个单变量随机变量,高斯分布的密度为:
p ( x ; μ , σ 2 ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) p\left(x ; \mu, \sigma^{2}\right)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) p(x;μ,σ2)=2πσ21exp(−2σ2(x−μ)2)
并且将近似后验建模为均匀分布:

其中 U ( y ~ i ; y i , 1 ) \mathcal{U}\left(\tilde{y}_{i} ; y_{i}, 1\right) U(y~i;yi,1)是以 y i y_i yi为中心的区间范围为1的均匀密度( y ~ i = y i + U ( 0 , 1 ) \tilde{y}_{i}=y_i+\mathcal{U(0,1)} y~i=yi+U(0,1))。
那么,该目标函数等效于我们的松弛率失真优化问题。KL散度中的第一项是0(这里的均匀分布概率密度函数值为1);第二项对应于失真(失真度量为MSE),第三项对应于率。
请注意,如果使用感知变换 g p g_p gp,或者度量 d d d不是欧几里得距离,则 p x ∣ y ~ p_{x|\tilde{y}} px∣y~不再是高斯分布,而是对应于密度:

其中 Z ( λ ) Z(\lambda) Z(λ)归一化密度。这无法保证与变分自动编码器的等价性,因为失真项可能不对应于可归一化的密度。
尽管这个非线性变换编码框架与变分自动编码器的框架相似,但有几个值得注意的基本差异:
首先,变分自编码器对连续值进行操作,而数字压缩则是在量化后离散域中进行。用微分熵的比特率替代离散熵的比特率可能会误导结果。为了能够端到端优化,这篇文章在连续域进行。但根据实验得到,离散与连续的率和失真相差不大。

其次,公式(13)中 λ λ λ是推断的。理想情况下 λ λ λ接近无穷大。而压缩模型必须在率失真曲线的任何给定点上进行,这是由权衡超参数 λ \lambda λ指定:

【左图:率失真权衡。灰色区域表示可以实现的所有率失真值的集合(在所有可能的参数设置上)。给定
λ
λ
λ选择的最优性能对应于该集的凸壳上的一个点,具有斜率
−
1
/
λ
−1/λ
−1/λ】
最后,尽管生成模型的典型松弛项(13)与率失真优化中的失真度量之间的对应关系仅仅适用于简单度量(如欧几里德距离),但从生成建模的角度来看,如果更一般的感知度量有对应的密度函数,则它也可以作为一种特殊的选择。
实验结果
作者将提出的方法与JPEG和JPEG 2000作比较。对于这篇论文提出的方法,所有图像均使用均匀量化进行量化(使用加性噪声的连续松弛仅用于训练目的)。另外,在推理阶段,作者还基于上下文的自适应二进制算术编码框架(CABAC;Context-Based Adaptive Binary Arithmetic Coding in the H.264/AVC Video Compression Standard,https://ieeexplore.ieee.org/document/1218195)实现了一个简单的熵编码(详细见原论文6.2)。




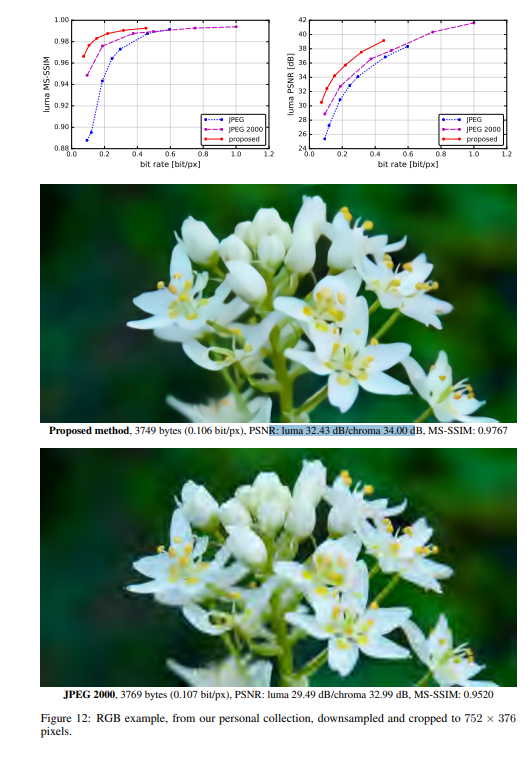







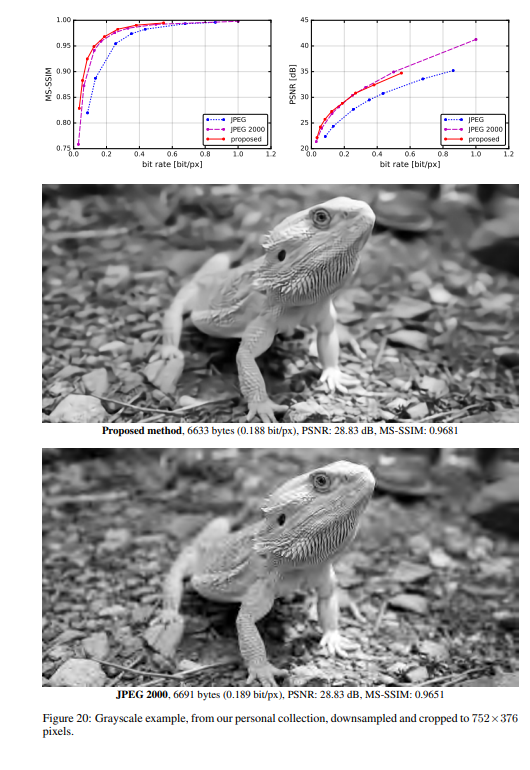


























 1122
1122

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










