SPSS回归分析（线性：一元（简单）和多重；非线性logistic）

通过评价实验得到主观数据，

然后通过描述性分析和显著性分析对这些数据的显著作用和影响趋势进行了判断.

最后一步就是针对这些数据，建立起可描述变量同主观感知结果之间的模型。

这个模型除了能够表征我们的数据 规律，还能够对已知变量分布的数据进行有效的 预测。

！！！！！！敲黑板啦！！！！！！！！！！！！！！

如果大家写主观实验相关论文的话，能够拔高这篇论文的层次的一个重要方面，就是有没有通过数据建立起来的模型。

！！！！！！！！！！！！！！！！！！！！！！！！！

首先是：

回归分析

从定义上说，回归分析是研究自变量与因变量之间数量变化关系的一种分析方法。

它主要是通过建立因变量Y与影响它的自变量Xi（i=1,2,3,…）之间的回归模型，衡量自变量Xi对于因变量Y的影响能力，进而可以用来预测因变量Y的发展趋势。

回归分析的一般步骤

1）根据预测目标，确定自变量和因变量；
2）绘制散点图，确定回归模型类型；
3）估计模型参数，建立回归模型；
4）对回归模型进行检验；
5）利用回归模型进行预测

一、线性模型（针对连续因变量，线性关系）

（一）简单线性回归（一元线性回归）

简单线性回归，也称为：一元线性回归。
就是回归模型中只有一个自变量，和我们的单因素分析相对应，它主要用来处理一个自变量和一个因变量之间的线性关系。

但更多情况下，我们要研究的因变量会受到很多自变量影响，那时需要后面的多重回归分析（多重回归分析记得看：调整后的R²，不是下面单纯的R²）。

一元线性回归的公式非常简单，就是一条直线方程，求截距（常数项）和自变量的系数，就是建立这个模型的方法：

线性回归的解法是，求解最佳的a和b，令尽可能多的样本数据点（Xi，Yi）落在或者靠近这条拟合出来的直线上，我们一般用最小二乘法，令观察点和估计点的距离的平方和最小。

这里面具体的解法我们就不研究了，大家只要知道，采用的是最小二乘法的解法即可。

在统计学应用领域有很多进行线性回归解法的案例，我们分析主观感知数据也可以参考这些案例，除了目的不同外，思路和方法都是一样的。

1、绘制散点图

举个例子，有一家超市连续3年的销售数据，包括：月份、季度、广告费用、客流量4个自变量和销售额1个因变量，共有36条记录。

下面我们从中 选择1个变量 进行一元线性回归的研究，这里可以选择广告费用，并绘制散点图进行观察。


然后在打开的对话框中，选择简单分布（默认），

Y轴是我们的因变量，销售额

X轴是我们想研究的广告费用，选择并按箭头导入

导入好数据后，点击确定，然后这个散点图就出现在输出窗口中啦

这个数据的分布近似一条直线对，所以可以做一元线性回归分析，那接下来咱们就建立模型。

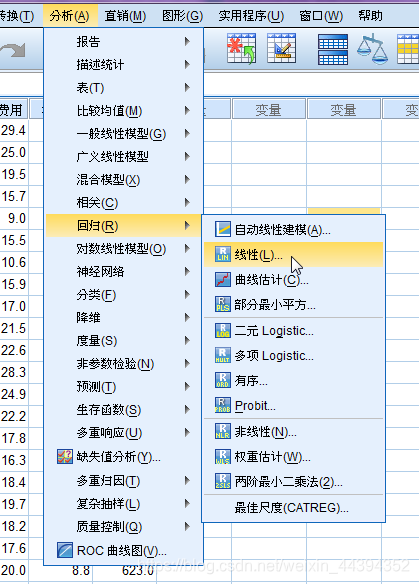
2、建立简单（一元）线性回归模型