使用SPSS 进行一元回归分析及应用

打开 SPSS 并导入数据

在SPSS中，使用 文件> 导入数据 > CSV 文件进行导入，在变量示图中保证输入的数据均为“标度“型数据。

绘制有关y与x的散点图

在数据模式下，点击图形> 旧对话框 > 散点图/点图，选择“简单散点图“的对话框，并将人均支出输出到y轴，人均收入输出到x轴，点击”确定”，spass会启动输出窗口，在输出窗口中查看生成的散点图。

进行一元线性回归分析

a) 在数据模式下，分析 > 回归 > 线性，进入回归的变量选择的对话框，对应因变量选择->人均支出y，自变量选择->人均收入x


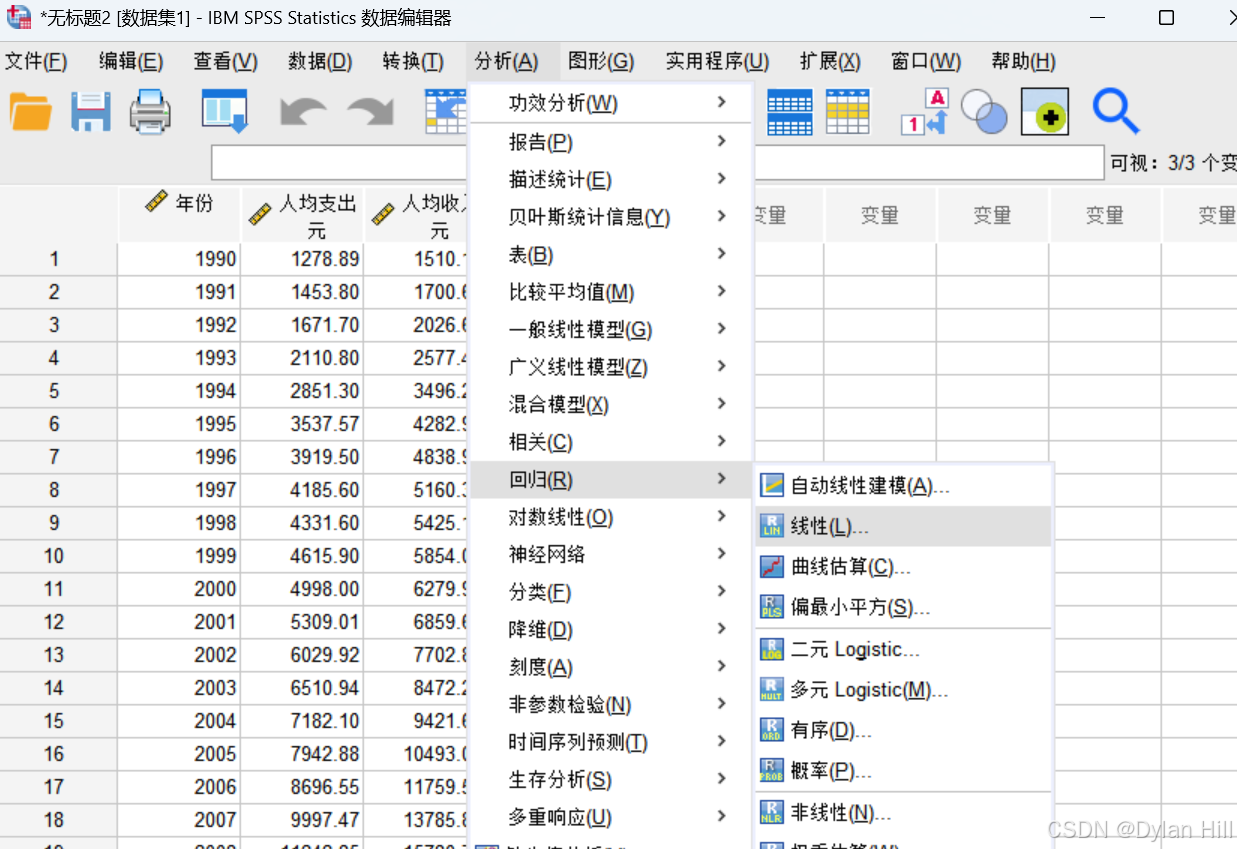
b) 在线性回归对话框，选择“统计(S)“ 在这个对话框，进行：回归系数：估算值，置信区间的选择；模型诊断需要有模型拟合(M)、R方的变化量、描述统计（D）的选择；

c) 在线性回归对话框，选择“图(T)“ 在这个对话框，进行残差图的输出：y轴选择的学生化残差”SRESID”，x轴选择自变量”DEPENDENT”,并保存正态概率图

Dependent (因变量): 这是指你指定的因变量的实际观测值。在输出或数据集中，它通常不会被改变或重新命名。
ZPRED (标准化预测值): 标准化的预测值是模型对因变量的预测值转换为标准正态分布后的值。这意味着ZPRED的平均值为0，标准差为1。
ZRESID (标准化残差): 标准化残差是将原始残差除以其估计的标准误得到的。标准化残差用于识别离群点，并且通常绝对值大于2的ZRESID可能表明该观测值是一个离群点。
DRESID (学生化删除残差): 学生化删除残差（Studentized deleted residuals）是在计算每个残差时，排除了当前观测值的影响。这是通过使用没有当前观测值的数据来重新拟合模型并计算残差实现的。这有助于识别那些对模型有较大影响的点。
ADJPRED (调整后预测值): 调整后预测值是基于所有其他观测值来预测某个特定观测值的结果，即不包括该观测值本身的信息。这种预测值可以用来评估模型对于特定数据点的稳定性。
SRESID (学生化残差): 学生化残差与ZRESID类似，但它是用剩余均方误差（MSE）除以未包含当前观测值的自由度来估计标准误。这同样用于检测离群点。
SDRESID (标准化删除残差): 标准化删除残差与DRESID相关，但是已经进行了标准化处理，使其具有零均值和单位标准差。
当你在SPSS中执行回归分析并选择了保存这些统计量时，SPSS会在你的数据集中创建相应的变量，并给它们赋予默认名称如ZPRED_1、ZRESID_1等。你可以通过查看这些新生成的变量来进一步分析模型的表现和诊断潜在的问题。

d) 在线性回归对话框，选择“保存（S）” 在这个对话框下要将输出的预测值，标准化\未标准化、残差的标准化和学生化残差均表留



e) 残差的正态性检验：残差的正态性检验检验的方式2:在数据视图模式下，分析->描述统计->探索->因变量列表：未标准化残差(RES_1)，显示（两者）->图(T) 含检验的正态图，点击确定。

f) 在数据视图下，针对x输入10000，重复上述步骤3将会输出对应的预测值

直接点确定即可，之前设置参数仍存在


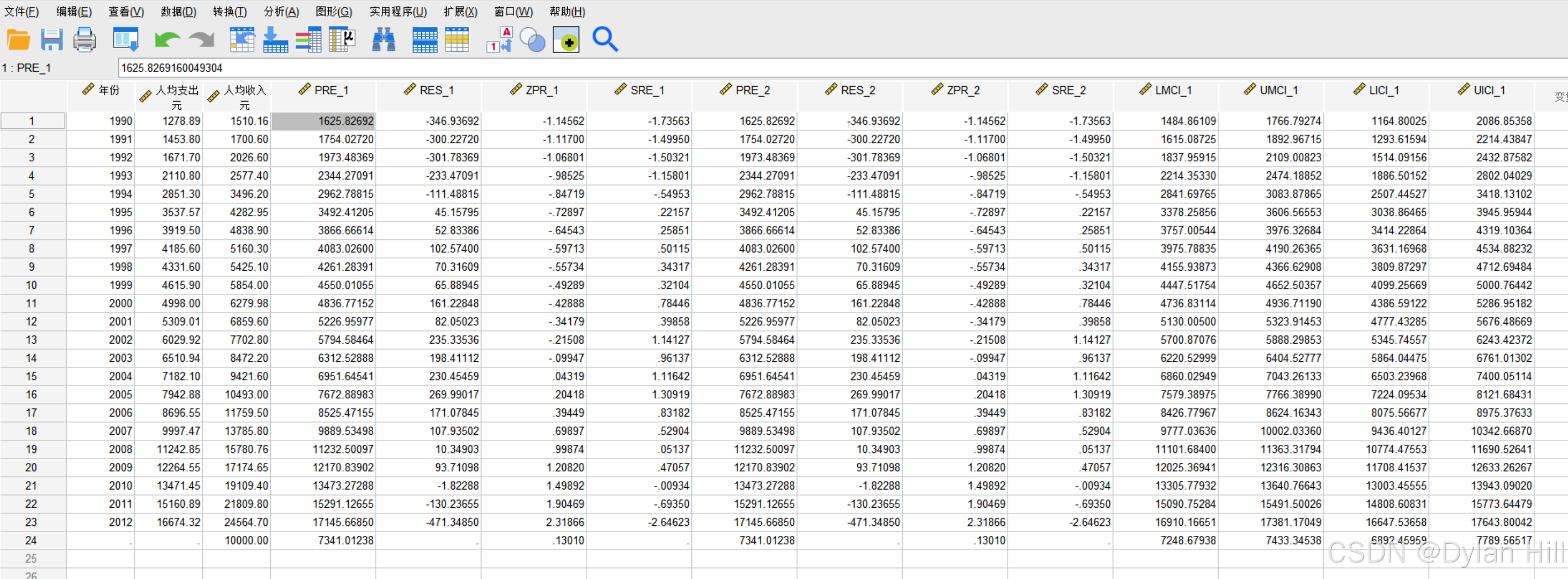
明显能看见为标准化预测值为7341.01238、标准化预测值0.13010
PRE_1: 这是未标准化预测值（Unstandardized Predicted Values）。它表示模型对因变量的预测值，即基于自变量计算出的因变量估计值。
RES_1 : 这是未标准化残差（Unstandardized Residuals）。它是观测值与预测值之间的差异，即实际观察到的因变量值减去模型预测的因变量值。

进行回归诊断，分析输出结果

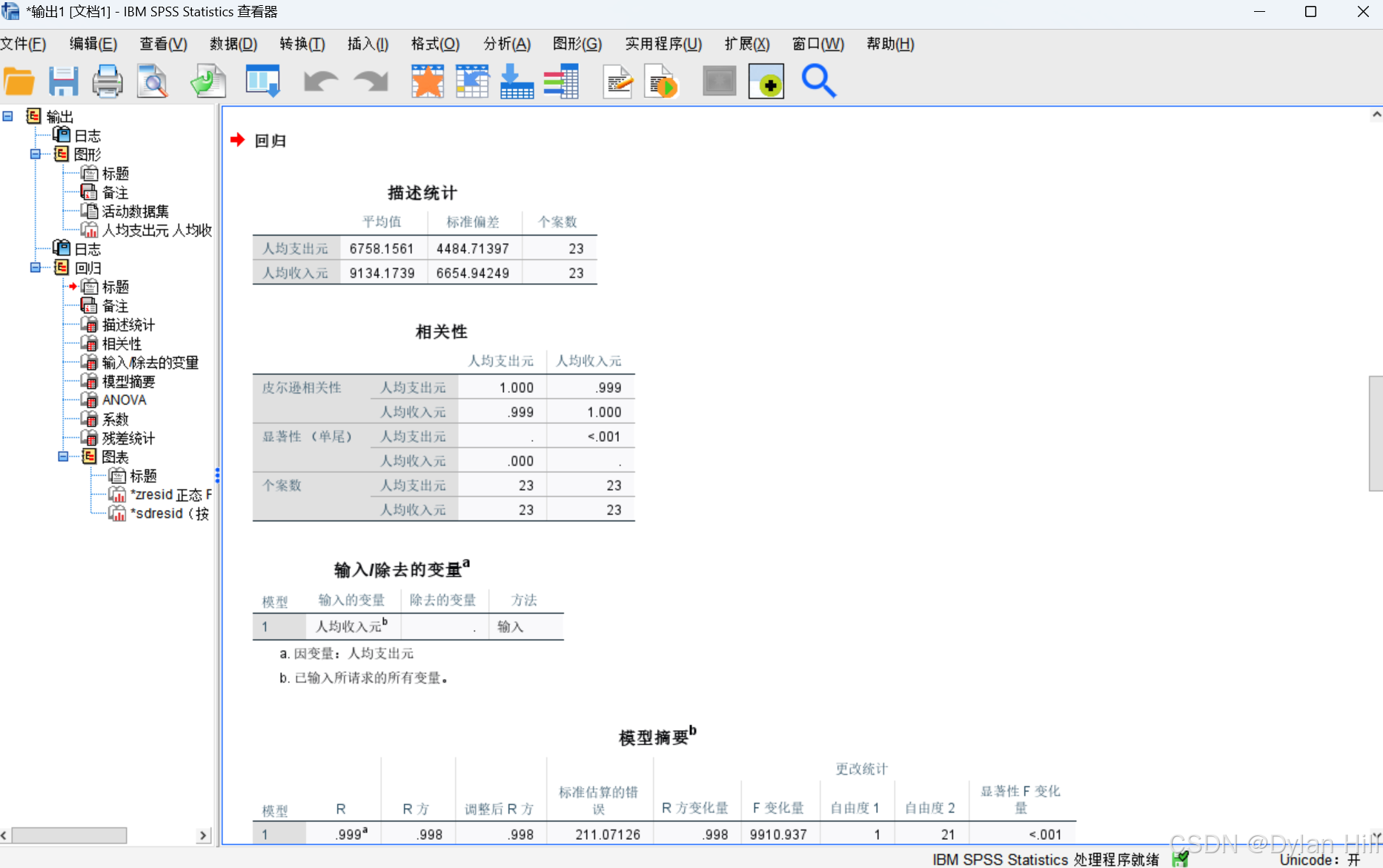
a)通过描述性统计，可以进一步了解样本的基础信息，如：有效样本量 N=23，人均收入的平均值=9134.1739，人均支出的平均值6758.1561；人均收入的标准差：6654.94249，人均支出的标准差4484.71397。

b) 通过相关系数表可以看到，人均收入和人均支出的相关系数r=0.999，单侧显著检验的概率值Sig.<0.001,说明y和x有显著的线性相关关系，与散点图显示一致。

c) 从模型摘要表可以看出，决定系数R方=0.998，从相对水平上看，回归方程能够减少因变量99.8%的方差波动，即因变量绝大部分都可以用方程解释，拟合优度好，回归标准差为211.07126，从绝对水平上看，将y的标准差从回归前的4484.71397减少到211.07126。

d) 从方差分析表可以看出，F=9910.937,显著性Sig.<0.001 ,说明y与x的线性回归高度显著，这与相关系数的检验结果一致。

e) 从相关系数表可以得出，回归方程y=609.218+0.673x，回归系数β1检验的t值为99.554，显著性Sig.<0.001,一元回归分析中F检验与相关系数r的检验结果一致，另外常数项β0的置信度为95%的区间估计为[451.497,766.939],回归系数β1的置信度为95%的置信区间估计为[0.659,0.687]。

f) 从残差图分析，回归分析计算出残差e，学生化残差SRE，在以自变量为横轴，学生化残差为y轴，由残差图可以看到所有点都在[-3,3]范围内，无异常值，但残差有自相关的趋势，当前姑且暂定残差满足基本假定的条件。由上述分析可知，样本数据基本正常，理论模型的假设是合适的

g) 残差的正态性检验：如果残差的分布在线的两侧说明残差符合正态分布的假定。

h) 模型应用，当所建立的模型通过所有的检验后，就可以结合实际的经济问题进行应用，最常见的应用之一就是因素分析，由回归方程可知，当城镇人均可支配的收入1元时，平均有0.673元由于支出消费，人均收入增长与支出的增长呈现正相关关系，符合实际经济意义。
设置x为10000后再次执行步骤三，其中保存->预测区间 打开平均值、置信区间，点击确定即可

针对10000，给出预测值以及置信区间
LMCI (Lower Mean Confidence Interval): 下限均值置信区间。这是对因变量的预测均值的下限估计。它表示在给定的置信水平（通常是95%）下，预测均值可能落在的最低值。
UMCI (Upper Mean Confidence Interval): 上限均值置信区间。这是对因变量的预测均值的上限估计。它表示在给定的置信水平（通常是95%）下，预测均值可能落在的最高值。
LICI (Lower Individual Confidence Interval): 下限个体置信区间。这是对单个新观测值的预测值的下限估计。它比均值置信区间更宽，因为它考虑了额外的变异，即新观测值的随机误差。
UICI (Upper Individual Confidence Interval): 上限个体置信区间。这是对单个新观测值的预测值的上限估计。同样，这个区间也比均值置信区间更宽，因为它包括了新观测值的随机误差。