SPSS系列2—简单线性回归

同样的，我还是在excel中构建简单的数据，再然后导入

1，【分析】-->【回归】-->【线性】

2，再点击分析-回归-线性，设置变量类型以及统计量等

统计量里选择：

绘制里选：

然后就是无脑出结果了，看看结果：

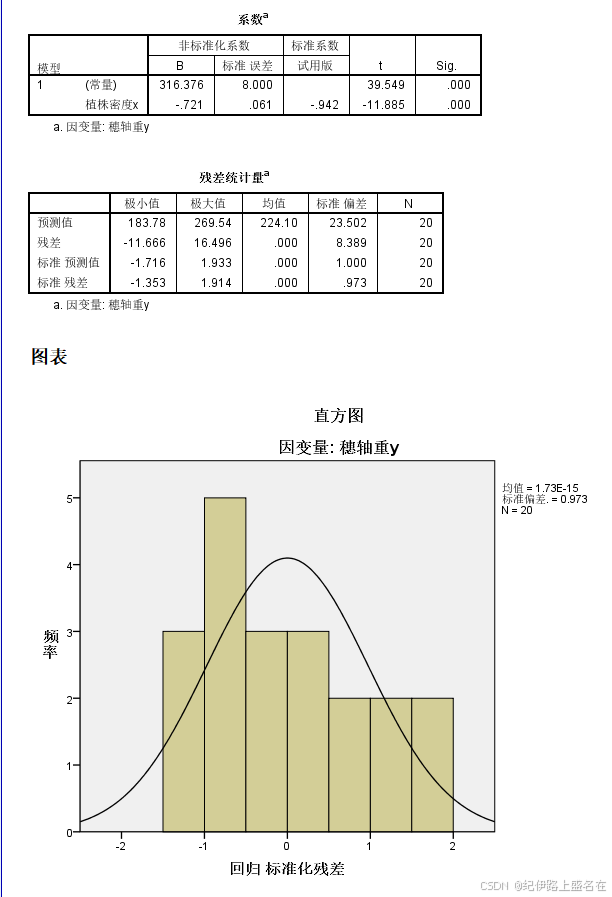
这里对于回归系数：截距项以及斜率项的估计，统计量以及显著性，以及拟合直线即估计模型的一些统计量，以及R square等都有；

再稍微复杂一点的非线性模型的拟合：
我们同样先打开并导入raw data：

我们的这个数据看上去一般

因为我们是做非线性拟合回归，

本质上就是对随机变量做一个映射，也就是非线性转换；

1，我们可以先查看线性模型拟合的效果如何：主要是查看斜率项的统计显著性，以及整体模型拟合的R square，当然相关系数也可以查看一下

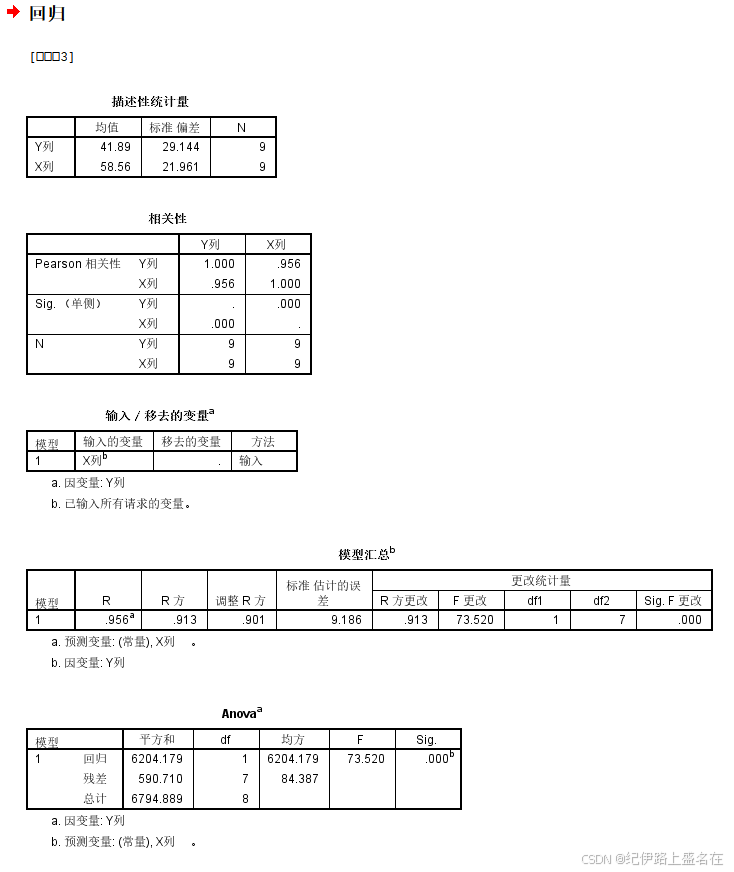
我们可以发现模型中回归系数斜率项的统计显著性还是很显著的，截距项的估计倒不是很显著；

另外就是模型的矫正R square有0.901，还是可以的；

2，接下来我们试一下非线性模型的拟合程度以及效果如何：

上面的非线性可以自己构建模型公式，但是还是建议使用曲线估计

首先是指数模型：

 

# 其余的部分实际上就是简单的同质性操作了，总体见下

1，

Ans：
此处不需要对卡方分布进行连续性矫正；

说白了就是卡方统计量46.988，自由度为6，然后P value可能下溢了，导致显示的效果看不见，总之就是有统计学显著性差异；

我们的H0是行列向量也就是变量不相关，然后这里显然是拒绝H0，所以我们的数据是认为行变量与列变量存在相关关系，

其实从原始数据上直观看，就是年龄越大，越难治，效果越不好。

2，

（1）第1个问题，我们只需要查看斜率项估计的显著性，我们可以看到非常显著，数值下溢到接近于0了

有拟合回归直线为：Y=-0.721*X+316.376

残差标准差近似值为：就是模型的残差项error的标准偏差，参考上面的表格就是8.389

（2）回归系数的显著性统计：

截距、截距项见（1），都是统计学显著的，回归系数斜率项表明：

植株密度每增加一个单位，穗轴重下降0.721g

（3）实际上就是模型的R square：

矫正R square是0.881，还行

3，

非线性变换的话有很多，实际上可以使用多种变换，比如说指数模型以及对数模型、幂函数模型等，以及高阶多项式模型；

首先是查看我们的数据的散点图分布形状如何：

我们可以先查看一下线性模型的拟合效果如何：

我们可以发现模型中回归系数斜率项的统计显著性还是很显著的，截距项的估计倒不是很显著；

另外就是模型的矫正R square有0.901，还是可以的；

接下来我们使用非线性模型拟合，比如说我使用指数模型：

 

指数模型本质上是对Y做了1个非线性变换，

然后获得了In Y和x的简单线性模型，同样获取非线性变换后简单线性回归模型的斜率以及截距项的估计值，以及对应的统计量，以及对应的统计显著性；

我们可以看到回归系数还是挺显著的，整体模型的矫正之后的R square也有0.964，还是挺不错的；

如果我用对数模型来拟合，结果则是：

回归系数都是挺显著的，但是模型整体的矫正R square降到了0.833，比简单线性回归还低

如果是做幂函数拟合：
 

我们可以发现回归系数中只有斜率项是统计学显著的，但是截距项并不显著；

但是整体模型的矫正之后的R square有0.972，还是挺不错的；

然后高阶多项式，比如说二次项，三次项等都可以尝试，但是这样回归系数就会比简单的线性多，就是多出来的几个线性低阶order项系数；

4，

实际上就是拟合logistic种群生长模型，本质上和前面的3没有多大区别；

因为此处并没有对因变量或者是自变量做一个哑变量的编码，因为实际上并没有哑变量的分类class信息在，

还是使用曲线拟合

本质上就是做了一个比较复杂的非线性变换，但是还是回归，回归系数还是简单一元的，可以看到系数还是比较统计学显著性的，另外模型整体的R square还是0.916，还是挺高的

5，

（1）对于Y1或者是Y2中的任何一个变量，进行简单的多远回归分析

然后因变量只有4个，

因为我们只是做简单的多元线性回归，所以模型还是线性估计

初步获取的结果如下：
 

我们可以看到实际上Y1拟合的简单多元线性回归模型中，

整体模型的矫正R square比较低，才只有0.494s

然后回归系数中基本上只有X2以及X4的系数是统计学显著性的，且X2系数是正的，X4系数是负的；

总体来说，对于Y1也就是对于低密度脂蛋白中的胆固醇含量和X2也就是载脂蛋白B的含量正相关（统计学显著性的），但是和载脂蛋白C的含量是负相关；

如果是对Y2进行的简单多元线性回归分析则有

模型统计结果如下：

我们可以发现

整体模型的矫正R square只有0.748，还行

然后回归模型的显著性上只有X1是统计学显著性的，且是正相关；

即对于Y2即高密度脂蛋白中的胆固醇含量与X1即·载脂蛋白A1的含量是正相关的，且统计学显著

（2）就是因为（1）中的问题，所以我们才需要进行逐步回归分析

SPSS实现逐步回归的基本步骤是，将变量一个一个引入，对引入的变量逐个进行检验，逐步剔除影响最不显著的自变量，直至将全部数据计算完毕，构造更优的回归方程。

比如说对于Y2

然后这里的显著性水平不变，方法中修改为逐步，其余的不变；

对于Y2的模型结果统计如下：

基本上我们可以发现：

基本上和前面一致，X1和X4显著，然后模型调整之后的整体R square是0.7左右，

而且将X3纳入之后比单独的X1构建的模型的可解释性增加

同样对Y1进行逐步回归分析：
获得的统计学结果如下，

基本上结论还是和前面（1）中一致，

X2、X4变量纳入到模型中，且正反相关关系基本上保持一致

但是模型的矫正R square比较低

参考：

【SPSS】回归分析详细操作教程（附案例实战）_spss回归分析-CSDN博客

SPSS多元线性回归及逐步回归教程_spss逐步回归-CSDN博客