透视投影和透视投影矫正

hhhcbw

于 2024-05-18 12:18:07 发布

阅读量556

点赞数 30

分类专栏：计算机图形学文章标签：图形渲染计算机图形学渲染游戏游戏引擎

本文链接：https://blog.csdn.net/weixin_44491423/article/details/139017304

版权

计算机图形学专栏收录该内容

1 篇文章 0 订阅

订阅专栏

透视投影是非线性变换

文章目录

透视投影
透视投影矫正
参考资料

透视投影

相较于正交投影(不管相距多远，物体大小不变)，透视投影更符合人眼观察世界的模式(近大远小)。

首先我们推导下投影到 $z = - d, d > 0$ 平面上的透视投影矩阵。

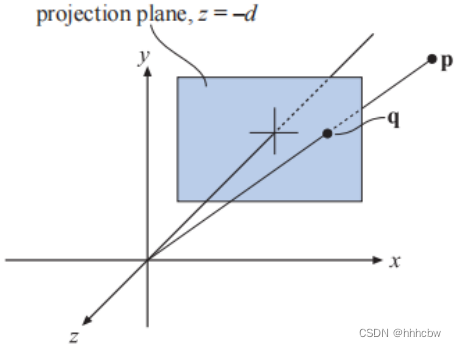
假设相机位于坐标原点(一般经过视图变换也确实位于坐标原点)，我们希望将点 $\bold{p}$ 投影到平面 $z = - d, d > 0$ 上，最终生成一个新的顶点 $\bold{q}=(q_x,q_y,-d)$ ，这个过程如上图所示。

通过图中的相似三角形，我们可以推导出点 $\bold{q}$ 的 $x$ 分量，如下所示

$\frac{q_x}{p_x}=\frac{-d}{p_z} \Longleftrightarrow q_x=-d\frac{p_x}{p_z} (1)$

同理也可以推出点 $\bold{q}$ 的 $y$ 分量为 $q_y=-d\frac{p_y}{p_z}$ ，将上述公式整合在一起，就可以获得这个透视投影矩阵 $\bold{M}_p$ ，具体如下所示

$\bold{M}_p=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & -1/d & 0 \end{pmatrix} (2)$

貌似与我们常见的透视投影矩阵不太一样，是因为我们经常使用的透视投影，并没有真正地将所有物体都投影到一个平面上(这个过程是不可逆的，会丢失深度值，后面的zbuffer没法处理)，而是将视锥体变换成了一个规则观察体。

我们会假设视锥体从 $z = n$ 开始，并在 $z = f$ 结束，其中 $0 > n > f$ 。在 $z = n$ 平面上，视锥体的截面是一个长方形，其最小角(左下角)是 $(l, b, n)$ ，最大角(右上角)是 $(r, t, f)$ ，同理 $z = f$ 平面上，视锥体的截面是一个更大的长方形，其最小角是 $(l, b, f)$ ，最大角是 $(r, t, f)$ 。

透视投影的整个过程，可以理解为：

将视锥体的远裁剪平面按一定规则，缩放到与近裁剪平面一样的尺寸，即将视锥体变成一个长方体；
然后再按照正交投影的方式，将其变换成一个规则观察体。

下面推导下视锥体变化为长方体的变换矩阵 $M_{persp \rightarrow ortho}$

考虑经过视图变换后的点坐标为 $x_v,y_v,z_v,1)^T$ ，那么经过 $M_{persp \to ortho}$ 我们希望这个点为 $nx_v/z,ny_v/z,?,1)^T$ 与其相同的齐次坐标为 $nx_v,ny_v,?,z)^T$ (考虑每一项乘上 $z_v$ )，具体公式可以写为

$M_{persp \rightarrow ortho}^{(4 \times 4)}\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right)=\left(\begin{array}{c} n x \\ n y \\ ？ \\ z \end{array}\right) (3)$

那么我们可以推出 $M_{persp \rightarrow ortho}$ 的部分项，即

$M_{persp \rightarrow ortho}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{array}\right) (4)$

再考虑所有在近平面的点都不会改变

远平面的在 $z$ 轴上的点也不会改变

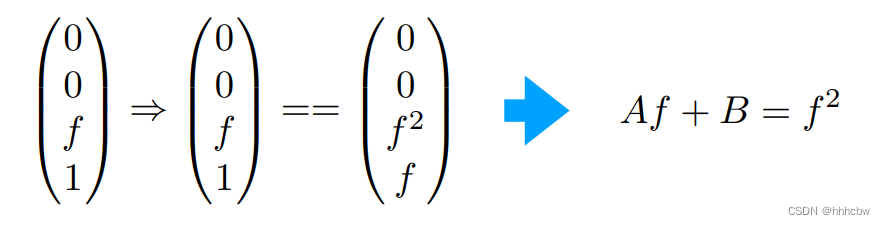
那么两变量，两个等式，就能求解出 $A$ 和 $B$

变换矩阵最终形式如下
$M_{persp \rightarrow ortho}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{array}\right) (5)$

当然我们可以乘上正交投影矩阵，得到最后的透视投影矩阵，在投影变换之后，还会进行裁剪操作和齐次化操作，最终将其转换到 NDC 空间中
$M_{persp}=M_{ortho}M_{persp \rightarrow ortho} = \left(\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & \frac{r+l}{l-r} \\ 0 & \frac{2}{t-b} & 0 & \frac{t+b}{b-t} \\ 0 & 0 & \frac{2}{n-f} & \frac{n+f}{f-n} \\ 0 & 0 & 0 & 1 \end{array}\right) \left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{array}\right) = \left(\begin{array}{cccc} \frac{2n}{r-l} & 0 & \frac{r+l}{l-r} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{b-t} & 0 \\ 0 & 0 & \frac{n+f}{n-f} & \frac{2nf}{f-n} \\ 0 & 0 & 1 & 0 \end{array}\right) (6)$

类似地，我们可以推出 OpenGL 的透视投影矩阵，需要注意的是，OpenGL 的视图空间是右手系，而齐次裁剪空间是左手系，所以其正交投影矩阵需要在一般的正交投影矩阵左乘一个镜像变换矩阵 $\bold{M}_o=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}$ ，最终的正交投影矩阵如下

$M_{orthoOpenGL} = \left(\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & \frac{r+l}{l-r} \\ 0 & \frac{2}{t-b} & 0 & \frac{t+b}{b-t} \\ 0 & 0 & \frac{2}{f-n} & \frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \end{array}\right) (7)$

同时，我们使用 $n^{'} = - n$ 以及 $f^{'} = - f$ 来替换，因为正的深度值更符合用户习惯，可以得到 OpenGL 的透视投影矩阵，远平面的点最终会投影到 $z = 1$ 平面，近平面的点最终会投影到 $z = - 1$ 平面

$M_{perspOpenGL} = \left(\begin{array}{cccc} \frac{2n'}{l-r} & 0 & \frac{r+l}{l-r} & 0 \\ 0 & \frac{2n'}{b-t} & \frac{t+b}{b-t} & 0\\ 0 & 0 & \frac{f'+n'}{f'-n'} & \frac{2f'n'}{f'-n'} \\ 0 & 0 & 1 & 0 \end{array}\right) (8)$

这个矩阵对点的作用其实是和 RealTime-Rendering-4th 中提到的 OpenGL 的透视投影矩阵是一样的，可能OpenGL里实际使用的是下面这种？

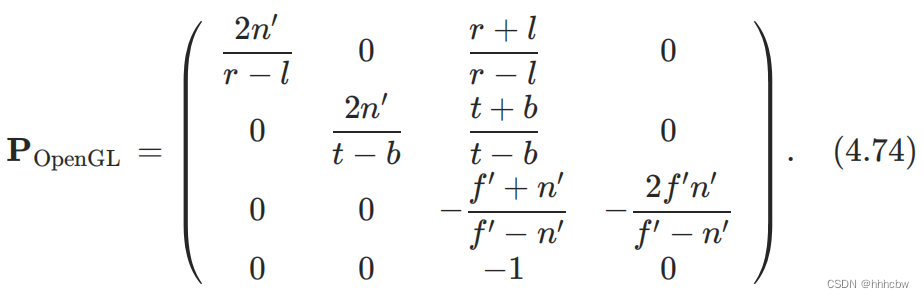
如果远裁剪平面设置在无穷远处 $\rightarrow \infty$ ，那么 $M_{persp}$ 将变成如下形式

$M_{perspInfty} = \left(\begin{array}{cccc} \frac{2n}{r-l} & 0 & \frac{r+l}{l-r} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{b-t} & 0 \\ 0 & 0 & -1& 2n \\ 0 & 0 & 1 & 0 \end{array}\right) (9)$

一般来说，对于透视投影，不提供 $l, r, b, t$ ，而是提供垂直视场角(FOV) $\phi$ 和宽高比 $a=\frac{w}{h}$ (代表了屏幕分辨率)，那么 $P_{OpenGL}$ 可以改为如下形式，其中 $c=\frac{1}{tan(\phi /2)}$

投影之后转换为 NDC 空间下，深度值其实是非线性变化的，导致远处点难以比较深度，可以通过反向z-buffer的手段等来提高深度值的精度

透视投影矫正

在使用光栅化的图形学方法中，法线，颜色，纹理坐标这些属性通常是绑定在图元的顶点上的，当我们需要除顶点外处的属性时，要通过插值的方式得到。

在3D空间中，这些属性值在图元应该是线性变换的。但是当3D顶点被透视投影到2D屏幕，如果在2D投影面上对属性进行线性插值，其对应的属性在3D空间中却不是线性变化的，下图可以明显看到， $c$ 是 $a$ 和 $b$ 的中点，但 $C$ 明显更靠近 $A$ ，这是因为透视投影是非线性变换

深度值插值

我们先以插值深度值为例，根据之前在透视投影的内容，我们知道 $X=\frac{Zu}{d}$ ，定义直线 AB 方程为 $ax+bz=c,c\ne0$

将 $X_t = \frac{Z_tu}{d}$ 代入AB的方程：

$a(Z_t\frac{u}{d})+bZ_t=c (10)$
$Z_t(a\frac{u}{d}+b)=c(11)$
$\frac{1}{Z_t}=\frac{au}{dc}+\frac{b}{c}(12)$

因为 $u=u_1+s(u_2-u_1)=u_1(1-s)+u_2s$ ，代入（12）

$\frac{1}{Z_t}=\frac{au_1(1-s)}{dc}+\frac{au_2s}{dc}+\frac{b}{c}=\frac{au_1}{dc}(1-s)+\frac{au_2}{dc}s+\frac{b}{c}(1-s)+\frac{b}{c}s(13)$
$\frac{1}{Z_t}=(\frac{au_1}{dc}+\frac{b}{c})(1-s)+(\frac{au_2}{dc}+\frac{b}{c})s(14)$

根据 (12) 有

$\frac{1}{Z_1}=\frac{au_1}{dc}+\frac{b}{c}(13)$
$\frac{1}{Z_2}=\frac{au_2}{dc}+\frac{b}{c}(14)$

代入（14）得

$\frac{1}{Z_t}=\frac{1}{Z_1}(1-s)+\frac{1}{Z_2}s(15)$

可以看出， $Z_t$ 的倒数是 $Z_1$ 倒数和 $Z_2$ 倒数的线性插值

考虑之前的透视投影矩阵 $P_{OpenGL}$ （这里 $r = - l, t = - b$ ，将第三列化简）我们将其应用到一个点可以得到

$P_{OpenGL}\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix}=\begin{pmatrix} \frac{2n'}{r-l}x\\ \frac{2n'}{t-b}y\\ -\frac{f'+n'}{f'-n'}z-\frac{2f'n'}{f'-n'}\\ -z \end{pmatrix}(16)$

z分量除以w分量，可以得到NDC空间下的z为 $\frac{A}{z}+B$ ，其中 $A=\frac{2f'n'}{f'-n'}$ ， $B=\frac{f'+n'}{f'-n'}$

所以NDC空间下的z，是和视图空间下的z成反比关系，可以直接在光栅化时进行插值。

我们将线性插值扩展到重心坐标插值，可以得到

$\frac{1}{Z_t}=\frac{1}{Z_1}(1-\alpha-\beta)+\frac{1}{Z_2}\alpha+\frac{1}{Z_3}\beta(17)$

顶点属性插值

对于顶点属性，我们可以有下面的比例关系
$\frac{I_t-I_1}{I_2-I_1}=\frac{Z_t-Z_1}{Z_2-Z_1}(18)$

而根据 (15)

$Z_t = \frac{1}{\frac{1}{Z_1}(1-s)+\frac{1}{Z_2}s}(19)$

代入到(18)，解出 $I_t$

$\frac{I_t-I_1}{I_2-I_1}=\frac{\frac{1}{\frac{1}{Z_1}(1-s)+\frac{1}{Z_2}s}-Z_1}{Z_2-Z_1}=\frac{1}{1+\frac{(1-s)Z_2}{sZ_1}}=\frac{Z_1s}{Z_1s+Z_2(1-s)}(20)$

$I_t = \frac{I_1Z_2(1-s)+I_2Z_1s}{Z_1s+Z_2(1-s)}(21)$

上下同除以 $Z_1 Z_2$ 得

$I_t=\frac{(1-s)\frac{I_1}{Z_1}+s\frac{I_2}{Z_2}}{(1-s)\frac{1}{Z_1}+s\frac{1}{Z_2}}(22)$

我们可以在透视投影之后的 w 分量取到视图空间中的 z 值，而不用单独保存下来

同样可以推广到重心坐标插值

$I_t=\frac{\frac{I_1}{Z_1}(1-\alpha-\beta)+\frac{I_2}{Z_2}\alpha+\frac{I_3}{Z_3}\beta}{\frac{1}{Z_1}(1-\alpha-\beta)+\frac{1}{Z_2}\alpha+\frac{1}{Z_3}\beta}(23)$