【 PMSM FOC、Clarke、Park、PI整定、前馈、弱磁、SVPWM、过调制、标幺化知识汇总】

weixin_44496201

已于 2024-03-22 00:10:28 修改

阅读量700

点赞数 3

文章标签：单片机嵌入式硬件

于 2024-03-20 00:14:36 首次发布

本文链接：https://blog.csdn.net/weixin_44496201/article/details/136858934

版权

`提示：本文为作者第一次发布博客，如有错误欢迎一起探讨！
本文为FOC框架的搭建,包括前馈、弱磁、PI参数、SVPWM、过调制以及系统标幺化。

# 前言

在写本文前，我一直在搭建FOC的模型，期间发现网上一些内容十分有帮助，我将其应用到模型中进行验证，最终分享给大家

---

# 一、FOC

在控制永磁同步电机时一般采用磁场定向控制，目的是控制电流电压产生旋转磁场带动转子进行转动，以下是我收集到的一些FOC的优点：
FOCField Oriented Control，磁场定向控制）控制方式具有以下优点：

转矩波动小
   FOC控制能够减少电机的转矩波动，从而提高电机的运行稳定性。
效率高
   通过精确控制磁场的大小和方向，FOC能够提高电机的效率，减少电能损耗。
噪声小
   由于电流波形的正弦化，FOC控制可以大幅减少电流谐波引起的噪声，从而使得电机运行更加安静。
动态响应快
   FOC控制能够快速响应负载变化，保持电机的平稳运行和快速加减速。
高精度控制
   FOC控制支持对电机转矩、速度、功率的精确控制，适用于多种应用场合。
可靠性和稳定性
   由于其高精度和快速响应的特性，FOC控制能够提供更稳定的电机运行和更长的使用寿命。
节能。通过精确控制磁场，FOC能够提高电机运行效率，节约电能。
无级调速
   FOC支持电机转速在一定范围内的无级调节，提供更灵活的控制选项。
保护机制健全
   FOC控制器包含多种保护功能，如过压、欠压、过流、过温等，以防止电机故障和安全事故。
寿命长
   由于采用电子换向技术，无电刷老化问题，同时减少轴承磨损，延长电机寿命。
尽管FOC控制具有众多优点，但其对控制器性能和电机参数的较高要求以及相对较高的硬件成本是其推广应用的挑战。

以下是网上抄的FOC的框图，先大概了解一下：

FOC框图

# 二、Clarke-Park 变换

在控制电机时，电机三相旋转电流计算起来总是太麻烦了，我们可以将之转化为直流电流，这就用到了clarke变换与Park变换
## 1.ClarkeTF

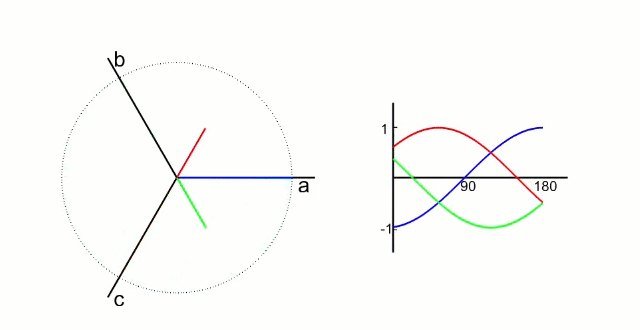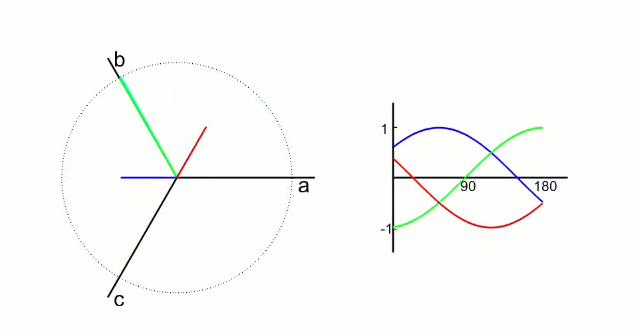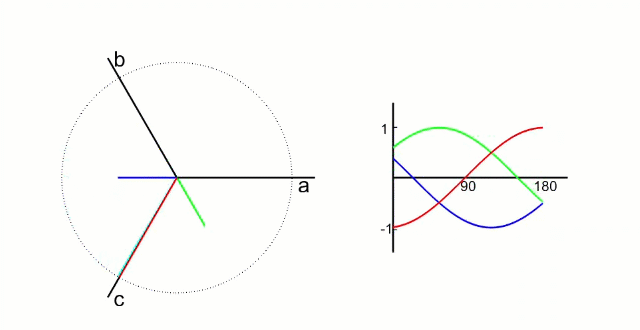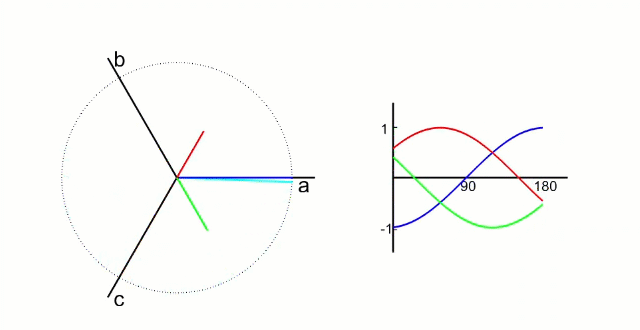
三相电流
上图可以直观的看到三相电流的波形

经过公式

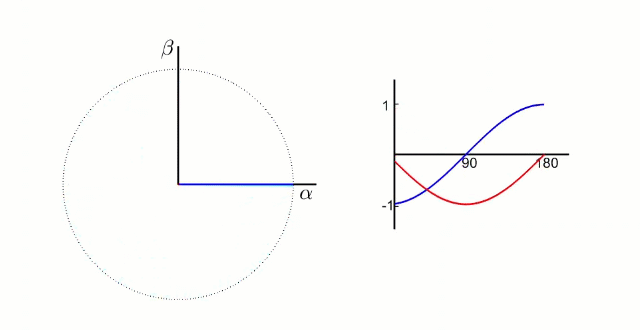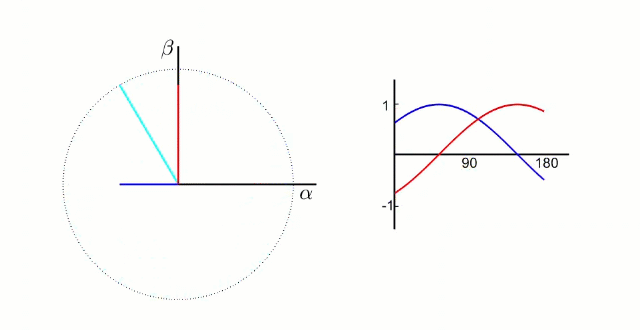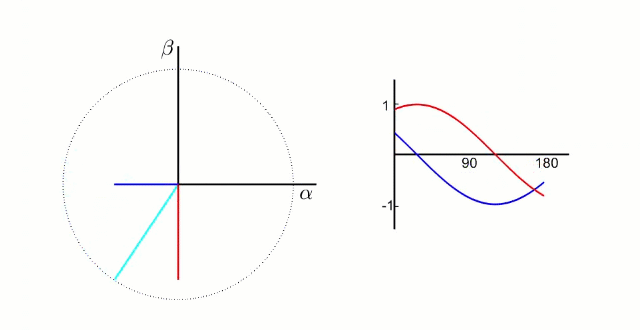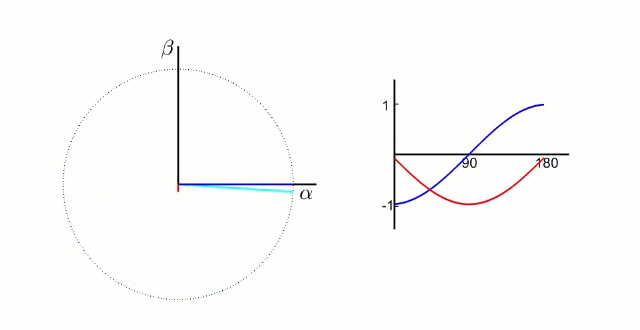
$\left\{\begin{matrix} I\alpha = Ia \\ I\beta =\frac{Ib - Ic}{\sqrt3}\end{matrix}\right.$

电流变为两相交流

闭路电路中，电流之和为0，也就是 Ia + Ib + Ic = 0,此为基尔霍夫电流定律

因此变换式可简化为：

$\left\{\begin{matrix} I\alpha = Ia \\ I\beta =\frac{Ia+2 \times Ib}{\sqrt3}\end{matrix}\right.$

Clarke变换公式

因为采电流时我采的是UW两相，因此这一步需要变换一下得到CurB

Matlab仿真

## 2.ParkTF

clark变换后经过下述公式将交流变为直流

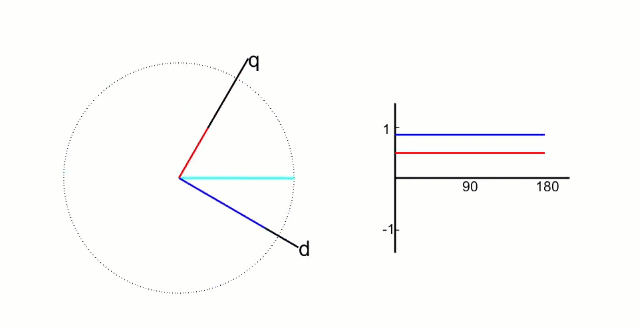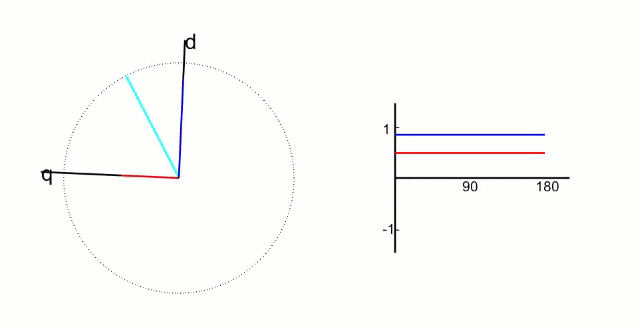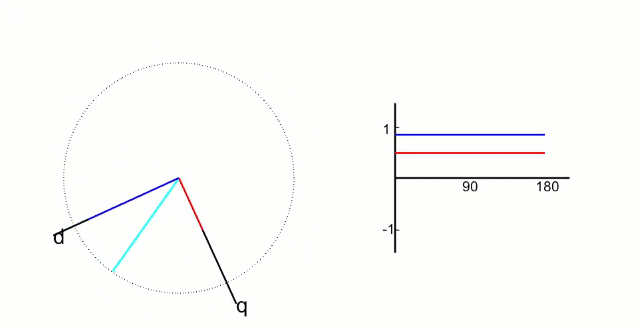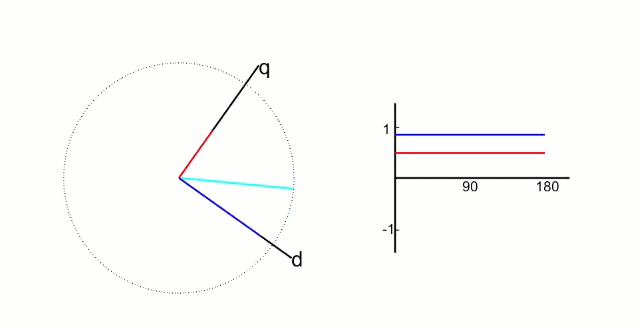
$\left\{\begin{matrix} Id = I\alpha \times cos\theta + I\beta \times sin\theta \\ Iq = I\beta \times cos\theta - I\alpha \times sin\theta \end{matrix}\right.$

Park变换交流变直流

Matlab仿真

#三、电流PI

2024.03.21更新

park变换出直流电后就可以进行电流环PI操作了，

#1、PID的模型搭建

我是用matlab搭建的PI，用的是位置式PID，还有增量式PID，增量式PID在写代码是可以省去一些资源，所以大多采样增量式。

$u\left ( k \right ) = k_{p} \times e\left(k\right) + k_{i} \times \sum _{i =0}^{k}e\left(i\right)+ k_{d}\times\left ([e\left(k\right) - e\left(k-1\right) \right ]$

位置式PID

$u\left ( k \right )-u\left ( k-1\right ) = k_{p} \times \left [e\left(k\right) - e\left(k-1\right) \right ]+ k_{i} \times e(k)+ k_{d}\times\left [e\left(k\right) - 2\times e\left(k-1\right) +e(k-2) \right ]$

增量式PID

位置式PID的Matlab仿真

# 2、Kp,Ki的整定

数学推导我就不讲的，网上一大堆，原理就是为了将电机的二阶系统降到一阶，最终对让

$\left\{\begin{matrix} K_{p} = \omega _{cc}Ls \\ K_{i}=\omega _{cc}T_{s}R_{s} \end{matrix}\right.$

其中wcc是PID截至频率，Ts是载波控制周期，Ls是电枢电感，Rs是电枢绕组电阻，

例如，我选的电机参数如下

%电机部分参数：
Rs = 0.05;
Ls = 0.000635;
Ts = 1e-4;
F = 1/Ts/20;
%Kp、Ki计算
Kp = 2*pi*F*Ls;
Ki = 2*pi*F*Ts*Rs;

其中截至频率F一般选择控制周期的1/20，也有选择1/10的，可以都试试效果，选择这个截至频率一般是看电机模型的频谱图得到的

例如如果系统为

则其Bode图为

可以根据图中的截至频率得到大概是wcc = 1000rad/s多点,因此F大概是300多，定一个附近的即可，也就是控制频率的1/20到1/10，

以上为我个人理解，具体细节不太清楚，我就是定了一个经验值1/20。

#四、前馈

电机的电压方程中可以了解到，DQ相有耦合的部分：

$U_{d} =I_{d}R_{s}+L_{d}\frac{dI_{d}}{dt}-\omega_{e}L_{q}I_{q}\\ U_{q} =I_{q}R_{s}+L_{q}\frac{dI_{q}}{dt}+\omega_{e}(\varphi _f+L_{d}I_{d})$

忽略动态项

$\left\{\begin{matrix} L_{d}\frac{dI_{d}}{dt} \\ L_{q}\frac{dI_{q}}{dt} \end{matrix}\right.$

可以看出其中

$\left\{\begin{matrix}\omega_{e}L_{q}I_{q} \\ \omega_{e}(\varphi _f+L_{d}I_{d}) \end{matrix}\right.$

为 Id Iq 耦合状态，将其解耦可以使PID相应更加迅速：

上图为Matlab的仿真模型。

在控制时，有时会发现其PI的结果不太理想，因此其中的Ld,Lq,Flux可以适当调整一番，

整定方法为，拖动电机至额定转速，开启电流环，给参考值均为0，此时会发现，只有Flux产生电压，Id Iq均为0，此时调节Flux参数，使PI输出在0附近。

调整好Flux后发现，稳态时前馈可完全代替PI输出，而PI基本不用起作用。

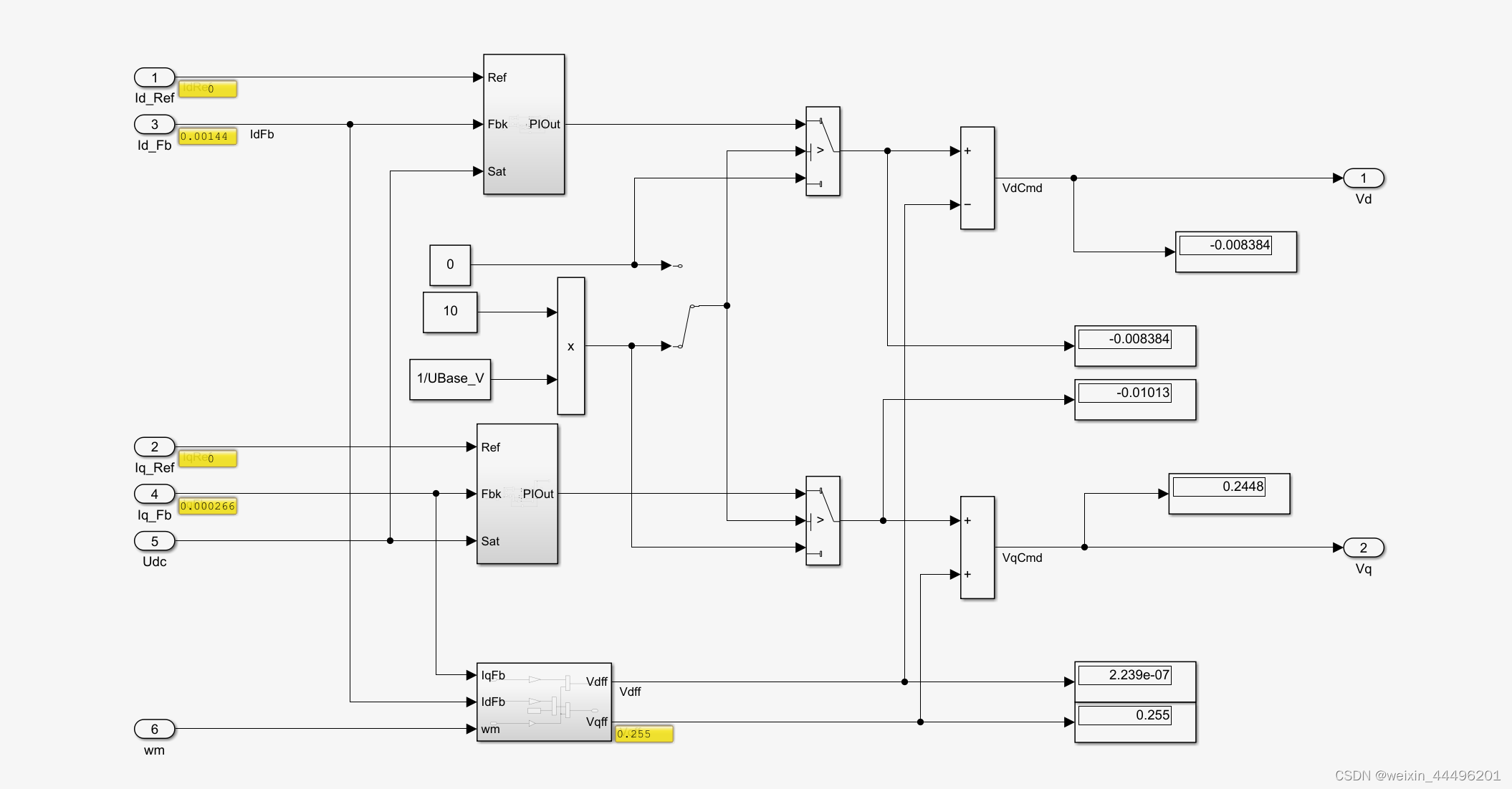
调整完Flux后，再调节Ld与Lq，调节方法为，给一个比较大的Q轴电流，此时D项为0，调整Lq,使D项PI为0左右，这时Lq就调整完毕。

同理，最后调Ld，给D轴电流，让Q项PI输出为0，至此前馈调节完毕。

2024.03.21,待续未完！

weixin_44496201

关注

3
点赞
踩
18

收藏

觉得还不错? 一键收藏
0
评论
【 PMSM FOC、Clarke、Park、PI整定、前馈、弱磁、SVPWM、过调制、标幺化知识汇总】

PMSM电机FOC控制算法研究
复制链接

扫一扫