【OpenCV 学习笔记】—— 基于拉普拉斯金字塔的图像融合原理以及C++实现【或许是全网最通俗易懂的讲解】

最新推荐文章于 2025-03-15 12:00:05 发布

凝望，划过星空.scut

最新推荐文章于 2025-03-15 12:00:05 发布

阅读量1w

点赞数 25

分类专栏： Learning OpenCV3 文章标签： opencv cv 计算机视觉

本文链接：https://blog.csdn.net/weixin_44586473/article/details/105893478

版权

Learning OpenCV3 专栏收录该内容

12 篇文章

订阅专栏

文章目录

一、高斯金字塔
- 1.1 什么是高斯金字塔
- 1.2 利用OpenCV求取高斯金字塔
二、拉普拉斯金字塔
- 2.1 什么是拉普拉斯金字塔
- 2.2 利用 OpenCV求取拉普拉斯金字塔
三、基于拉普拉斯金字塔的图像融合

一、高斯金字塔

1.1 什么是高斯金字塔

其实大家也不要被 “金字塔” 这样看起来高大上的名词给唬住了。其实说白了，高斯金字塔就是原始图像按照一定的方式缩小若干次所得到的一系列图像罢了。我们只是将缩小的每一幅图像比作金字塔的每一层。但是，我们还没说：到底是什么方式呢？

对同一尺寸的图像，进行高斯平滑以及下采样再平滑、、、构成的所有图像集合才构成了图像的高斯金字塔。

如下图所示，一般高斯金字塔从第 0 级开始，第 0 级就是原图大小，金字塔级数越高，图像的分辨率就越底。所以说，图像金字塔也是图像多尺度表达的一种方式。
在这里插入图片描述
那么，说到这儿，其实构建高斯金字塔的思路也很明确了：（以求取地 $i + 1$ 层高斯金字塔的步骤如下）

先对第 $i$ 层高斯金字塔图像做高斯平滑
将所有偶数行和列去除

我们可以发现第 $i + 1$ 层金字塔的图像是第 $i$ 层金字塔图像大小的四分之一。同时，因为下采样的原因，会造成图像信息的丢失。值得注意的是，对一张图像下采样之后再上采样回原来的大小，所得的图像将不再是原来的图像了，也就是说：下采样和上采样不是互为可逆的过程！

1.2 利用OpenCV求取高斯金字塔

Opencv 里面提供了 PyrUp 和 PyrDown 函数，不过在我们一会儿展示的代码中使用的是 PyrDown 函数。

void pyrDown(InputArray src, OutputArray dst, const Size& dstsize=Size());

第一个参数 scr：输入的图像
第二个参数 dst：返回的图像
第三个参数：这个参数指的是降采样之后的目标图像的大小，我们可以看出它是有默认值的，如果我们调用函数的时候不指定第三个参数，那么这个值是按照 Size((src.cols+1)/2, (src.rows+1)/2) 计算的

我们来看看这个 PyrDown 函数到底在干嘛—— PyrDown 的作用是先对图像进行高斯平滑，然后再进行降采样（将图像尺寸行和列方向缩减一半）； 这不正是我们构建高斯金字塔所需要的步骤嘛！

下面上代码：

//-------------------Function 1 高斯金字塔的构建------------------------//
vector<Mat> bulid_Gaussian_Pyr(Mat& input, vector<Mat> Img_pyr, int level)
{
	/*
	参数说明:
	参数1: 输入的 Mat 类型待求高斯金字塔图像
	参数2: 输出的高斯金字塔(以 vector<Mat> 类型保存, 可使用.at()获取某一层的内容)
	参数3: 高斯金字塔的级数( 此处应特别注意:真实的层数是 level + 1 !)
	*/
	
	Img_pyr.push_back(input);
	Mat dst;
	for(int i = 0; i < level; i++)
	{
		pyrDown(input, dst, Size(input.cols/2, input.rows/2));
		Img_pyr.push_back(dst);
		input = dst;
	}
	return Img_pyr;
}

二、拉普拉斯金字塔

2.1 什么是拉普拉斯金字塔

与其说是拉普拉斯金字塔，不如叫做残差金字塔。因为我们刚刚不是说了吗，图像的降采样和上采样不是可逆的。那么拉普拉斯金字塔的构建方法如下图所示：

假设高斯金字塔就 3 个 level（0， 1，2），那么，我们先把高斯金字塔的最高层（最小的那个）上采样（放大）。我们知道，上采样之后和原金字塔第 1 个 level相比是有信息丢失的，我们就把原高斯金字塔的第 1 个level 的图像和这个经过第 2 个level 图像上采样得到的图像相减（第 2 个 level 图像上采样之后就和原高斯金字塔第 1 个 level 图像的大小一样了），相减就会得到一个残差，这就是拉普拉斯金字塔的最高级（下图中就应该是 level 1）。

同样地，把原高斯金字塔的 level 0 的图像和原高斯金字塔 level 1 经过上采样得到的图像相减，就得到了拉普拉斯金字塔的第 0 层。至此，下图所示的拉普拉斯金字塔就构建完毕了。

值得注意的是：如果一幅图像的高斯金字塔有 N+1 层，那么其对应的拉普拉斯金字塔就有 N 层
在这里插入图片描述

2.2 利用 OpenCV求取拉普拉斯金字塔

这里我们就同时需要用到 PyrDown 和 PyrUp 了，我们下面看一下代码：

//---------------------------------Function 2 拉普拉斯金字塔的构建---------------------------------------------------------//
vector<Mat> bulid_Laplacian_Pyr(vector<Mat> Img_Gaussian_pyr, vector<Mat> Img_Laplacian_pyr, int level)
{
	/*
	参数说明:
	参数1: 输入的高斯金字塔 vector<Mat> 类型，每一个元素代表每一层
	参数2: 待求解的拉普拉斯金字塔
	参数3: 拉普拉斯金字塔的层数 level
	*/
	
	vector<Mat> Img_Gaussian_pyr_temp;
	Img_Gaussian_pyr_temp.assign(Img_Gaussian_pyr.begin(), Img_Gaussian_pyr.end());   //由于vector对象不能使用=拷贝，此处使用assign进行复制
	
	Mat for_sub, for_up;                  
	for(int i = 0; i < level; i++)
	{
		Mat for_up = Img_Gaussian_pyr_temp.back();       //获取高斯金字塔当前最高层的图像的引用
		Img_Gaussian_pyr_temp.pop_back();                //删除最后一个元素
		
		for_sub = Img_Gaussian_pyr_temp.back();          //获取被减数图像

		Mat up2;
		pyrUp(for_up, up2, Size(for_up.cols * 2, for_up.rows * 2));    //上采样

		Mat lp;
		/*
		cout<<"尺寸1"<<for_sub.size();
		cout<<"c尺寸2"<<up2.size();
		*/
		lp = for_sub - up2;
		Img_Laplacian_pyr.push_back(lp);
	}
	reverse(Img_Laplacian_pyr.begin(),Img_Laplacian_pyr.end());       //做一下反转(0->最大尺寸的金字塔层)
	return Img_Laplacian_pyr;
}

三、基于拉普拉斯金字塔的图像融合

3.1 融合原理

在说融合之前，我们需要说一下什么是 mask（掩膜），这里为了方便理解，请暂且允许我简单地先把它理解为融合图像的权重（因为融合其实可以看成是一个加权求和的过程）。下面我们一步一步看一下到底是如何通过拉普拉斯金字塔做图像融合的：（设待融合的两幅图像分别为 $I m g 1, I m g 2$ ）

【Step 1】：传入一个 mask掩膜（作为一会两幅待融合图像相加的权重，其实就是一个 Mat）

【Step 2】：分别计算 $I m g 1$ 和 $I m g 2$ 的高斯金字塔和拉普拉斯金字塔（以 $I m g 1$ 为例）
在这里插入图片描述
【Step 3】计算得到 mask 的高斯金字塔

【Step 4】将 $I m g 1$ 和 $I m g 2$ 高斯金字塔的顶层按照 mask 的权重（mask高斯金字塔的顶层）相加，得到复原的起点，记为 $S T A R T$

【Step 5】将 $I m g 1$ 和 $I m g 2$ 的拉普拉斯金字塔每一层按照 mask 权重相加（mask高斯金字塔对应的层），得到混合的拉普拉斯金字塔 $Blend\_lp$

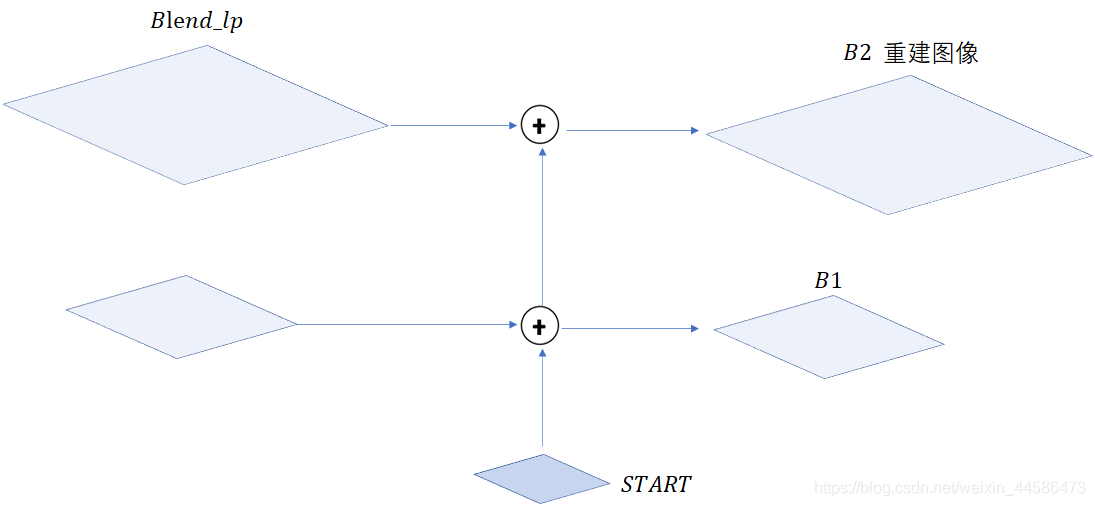
【Step 6】根据这个新的金字塔重建出最终的图像，具体来讲，先对 $S T A R T$ 进行上采样，然后跟混合拉普拉斯金字塔 $Blend\_lp$ 的顶层相加，得到 $B 1$ ，然后 $B 1$ 继续上采样，在和 $Blend\_lp$ 的下一层相加，得到 $B 2$ 、、、重复上述过程，最终得到融合的图像
在这里插入图片描述

3.2 代码实现

下面给出完整的代码：

//----------------------------基于拉普拉斯金字塔的图像融合算法---------------------------//
//Configuration: Visual Studio 2010 + Opencv2.4.10
//Author: 周子豪 / South China University of Technology 
//Date: 2020.5.2

#include <opencv2/opencv.hpp>
#include<vector>
#include<iostream>


using namespace std;
using namespace cv;

vector<Mat> bulid_Gaussian_Pyr(Mat& input, vector<Mat> Img_pyr, int level);
vector<Mat> bulid_Laplacian_Pyr(vector<Mat> Img_Gaussian_pyr, vector<Mat> Img_Laplacian_pyr, int level);
vector<Mat> blend_Laplacian_Pyr(vector<Mat> Img1_lp, vector<Mat> Img2_lp,vector<Mat> mask_gau, vector<Mat> blend_lp);
Mat blend(Mat& result_higest_level, vector<Mat> blend_lp);

int main()
{
	vector<Mat> Gau_Pyr, lp_Pyr, Gau_Pyr2, lp_Pyr2;
	vector<Mat> maskGaussianPyramid; 

	Mat input = imread("4.jpg", 1);
	Mat input2 = imread("test11.jpg", 1);

	imshow("待融合图像1", input);
	imshow("待融合图像2", input2);

	resize(input,input,Size(600, 600));
	
	int height = input.rows;
	int width = input.cols;
	//cout<<"width"<<width<<endl;
	//cout<<"height"<<height<<endl;

	resize(input2, input2, Size(600,600));

	input.convertTo(input, CV_32F);                  //转换成CV_32F, 用于和mask的类型匹配( 另外 CV_32F 类型精度高, 有利于计算)
	input2.convertTo(input2, CV_32F);

	Gau_Pyr = bulid_Gaussian_Pyr(input, Gau_Pyr,3);       //计算两张图片的高斯金字塔
	Gau_Pyr2 = bulid_Gaussian_Pyr(input2, Gau_Pyr2,3);
	
	/*
	imshow("高斯金字塔第0层", Gau_Pyr.at(0));
    imshow("高斯金字塔第1层", Gau_Pyr.at(1));
	imshow("高斯金字塔第2层", Gau_Pyr.at(2));
	imshow("高斯金字塔第3层", Gau_Pyr.at(3));
	*/
	lp_Pyr = bulid_Laplacian_Pyr(Gau_Pyr, lp_Pyr, 3);     //计算两者图像的拉普拉斯金字塔
	lp_Pyr2 = bulid_Laplacian_Pyr(Gau_Pyr2, lp_Pyr2, 3);
	
	/*
	imshow("拉普拉斯金字塔第0层", lp_Pyr.at(0));    //当然,使用blend_lp[0]也是可以的
	imshow("拉普拉斯金字塔第1层", lp_Pyr.at(1));
	imshow("拉普拉斯金字塔第2层", lp_Pyr.at(2));
        */

	
	Mat mask = Mat::zeros(height, width, CV_32FC1);           //构造掩膜mask, CV_32FC1类型, 大小和 Img1 一样
	mask(Range::all(), Range(0, mask.cols * 0.5)) = 1.0;      //mask的所有行,然后左半部分是1,右半部分是0 (意思是对半融合)

	cvtColor(mask, mask, CV_GRAY2BGR);                        //因为此时mask是单channel的,Img是3channel的,所以还需要cvtColor

	//cout<<"现在mask的type"<<mask.type()<<endl;
	//cout<<"现在的lp的type"<<lp_Pyr.at(0).type()<<endl;

	vector<Mat> mask_Pyr, blend_lp;

	Mat result_higest_level;                                  //图像融合的起点
	
	mask_Pyr = bulid_Gaussian_Pyr(mask, mask_Pyr, 3);         //mask的高斯金字塔也是 level+1 层的
	
	//下面将 Img1, Img2的高斯金字塔的顶层按照mask融合
	result_higest_level = Gau_Pyr.back().mul(mask_Pyr.back()) + ((Gau_Pyr2.back()).mul(Scalar(1.0, 1.0, 1.0) - mask_Pyr.back()));
	
	/*
	imshow("mask高斯金字塔的第0层", mask_Pyr.at(0));
	imshow("mask高斯金字塔的第1层", mask_Pyr.at(1));
	imshow("mask高斯金字塔的第2层", mask_Pyr.at(2));
	imshow("mask高斯金字塔的第3层", mask_Pyr.at(3));
	*/

	blend_lp = blend_Laplacian_Pyr(lp_Pyr, lp_Pyr2, mask_Pyr, blend_lp);

	/*
	imshow("融合拉普拉斯金字塔的第0层", blend_lp.at(0));
	imshow("融合拉普拉斯金字塔的第1层", blend_lp.at(1));
	imshow("融合拉普拉斯金字塔的第2层", blend_lp.at(2));
	*/
	imshow("图像融合的起点", result_higest_level);

	Mat output;
	output = blend(result_higest_level, blend_lp);
	output.convertTo(output, CV_8UC3);
	imshow("融合效果图", output);

	waitKey();
	return 0;
}

//-------------------Function 1 高斯金字塔的构建------------------------//
vector<Mat> bulid_Gaussian_Pyr(Mat& input, vector<Mat> Img_pyr, int level)
{
	/*
	参数说明:
	参数1: 输入的 Mat 类型待求高斯金字塔图像
	参数2: 输出的高斯金字塔(以 vector<Mat> 类型保存, 可使用.at()获取某一层的内容)
	参数3: 高斯金字塔的级数( 此处应特别注意:真实的层数是 level + 1 !)
	*/
	
	Img_pyr.push_back(input);
	Mat dst;
	for(int i = 0; i < level; i++)
	{
		pyrDown(input, dst, Size(input.cols/2, input.rows/2));
		Img_pyr.push_back(dst);
		input = dst;
	}
	return Img_pyr;
}

//---------------------------------Function 2 拉普拉斯金字塔的构建---------------------------------------------------------//
vector<Mat> bulid_Laplacian_Pyr(vector<Mat> Img_Gaussian_pyr, vector<Mat> Img_Laplacian_pyr, int level)
{
	/*
	参数说明:
	参数1: 输入的高斯金字塔 vector<Mat> 类型，每一个元素代表每一层
	参数2: 待求解的拉普拉斯金字塔
	参数3: 拉普拉斯金字塔的层数 level
	*/
	
	vector<Mat> Img_Gaussian_pyr_temp;
	Img_Gaussian_pyr_temp.assign(Img_Gaussian_pyr.begin(), Img_Gaussian_pyr.end());   //由于vector对象不能使用=拷贝，此处使用assign进行复制
	
	Mat for_sub, for_up;                  
	for(int i = 0; i < level; i++)
	{
		Mat for_up = Img_Gaussian_pyr_temp.back();       //获取高斯金字塔当前最高层的图像的引用
		Img_Gaussian_pyr_temp.pop_back();                //删除最后一个元素
		
		for_sub = Img_Gaussian_pyr_temp.back();          //获取被减数图像

		Mat up2;
		pyrUp(for_up, up2, Size(for_up.cols * 2, for_up.rows * 2));    //上采样

		Mat lp;
		/*
		cout<<"尺寸1"<<for_sub.size();
		cout<<"c尺寸2"<<up2.size();
		*/
		lp = for_sub - up2;
		Img_Laplacian_pyr.push_back(lp);
	}
	reverse(Img_Laplacian_pyr.begin(),Img_Laplacian_pyr.end());       //做一下反转(0->最大尺寸的金字塔层)
	return Img_Laplacian_pyr;
}

//------------------------------------Function 3 混合拉普拉斯金字塔的构建-----------------------------------------//
vector<Mat> blend_Laplacian_Pyr(vector<Mat> Img1_lp, vector<Mat> Img2_lp,vector<Mat> mask_gau, vector<Mat> blend_lp)
{
	/*参数说明:
	参数1: 待融合图像1的拉普拉斯金字塔 vector<Mat> 类型(level 层)
	参数2: 待融合图像2的拉普拉斯金字塔 vector<Mat> 类型
	参数3: mask掩膜的高斯金字塔 (level+1层)
	参数4: 待返回的混合拉普拉斯金字塔 vector<Mat> 类型
	*/

	int level = Img1_lp.size();

	//cout<<"level"<<level;  确认level级数 

	for(int i = 0; i < level; i++)                                        //注意 0 表示最大的图，说明是从底开始融合lp
	{  
		Mat A = (Img1_lp.at(i)).mul(mask_gau.at(i));                      //根据mask(作为权重) 
		
		Mat antiMask = Scalar(1.0, 1.0, 1.0) - mask_gau[i];
		Mat B = Img2_lp[i].mul(antiMask);
		Mat blendedLevel = A + B;                                         //待融合图像的拉普拉斯金字塔对应层按照mask融合
		blend_lp.push_back(blendedLevel);                                 //存入blend_lp, 作为第 i 层
	}
	return blend_lp;
}

//--------------Function 4 图像融合---------------------//
Mat blend(Mat& result_higest_level, vector<Mat> blend_lp)
{
	/*参数说明:
	参数1: 图像混合的起点Mat (也就是两个带融合图像高斯金字塔最高层按mask加权求和的结果
	参数2: Function 3所求得的混合拉普拉斯金字塔 vector<Mat> 类型
	*/

	int level = blend_lp.size();      
	Mat for_up, temp_add;
	for(int i = 0; i < level; i++)
	{	
		pyrUp(result_higest_level, for_up, Size(result_higest_level.cols * 2, result_higest_level.rows * 2));
		temp_add = blend_lp.back() + for_up;
		blend_lp.pop_back();              //因为此处是直接删除最后一个元素,所以在调用本函数之前如后续的代码还需要blend_lp, 需要先行保存拷贝
		result_higest_level = temp_add;
	}
	return temp_add;
}