工程/物理光学
【工程/物理光学(一)——光的电磁理论基础】
【工程/物理光学(三)——光的干涉】
【工程/物理光学(四)——光的衍射技术】
【工程/物理光学(五)——激光技术】
本文作为个人《物理光学》的学习记录,仅希望能够用较为简单的方法来阐述和理解物理光学,不涉及许多高深的物理公式推导,本文主要参考书为清华大学出版社1、范希智老师的《物理光学》和2、田芊等老师的《工程光学》
一、几何光学原理
1、实验三定律
实验三定律由人们在长期科学实践当中总结得出,包括:光的直线传播定律、反射定律和折射定律。
- 光的直线传播定律:光在均匀介质中沿直线传播;
- 反射定律:当光入射至两种不同透明介质的分界面上时,一部分光会反射回入射光所在的介质,且入射角等于反射角;
- 折射定律:当光入射至两种不同透明介质的分界面上时,除了反射回去的反射光外,还有另外一部分折射光会越过界面进入另一种介质,即发生折射现象。
折射定律和反射定律详细可参看上一篇《工程/物理光学——光的电磁理论基础》
注:另外光路可逆原理指的是,当光沿反方向传播,必定沿原光路返回。
2、费马原理
费马在1650年将上述实验三定律总结归纳为费马原理。首先引入光程的概念:将光在介质中传播的路程
d
d
d与介质折射率
n
n
n的乘积定义为光程
δ
\delta
δ:
δ
=
n
d
\delta=nd
δ=nd
其中
t
t
t为光的传播时间,根据折射率的定义(即真空中光速与介质中光速的比值)不难得到,即光传播的光程完全由其传播时间
t
t
t决定:
δ
=
c
t
\delta=ct
δ=ct
进一步,就可以将费马原理表示为:光总是沿着光程为极值的路径传播。注意:一般为极值为极小值和恒定值,也可能为极大值。
二、光学成像
1、基本概念
通过物点和光轴的截面叫子午面,轴上物点的子午面有无数个,而轴外物点的子午面只有一个。在子午面内,物方光线 A E AE AE的位置由以下两参数确定(如下图所示):
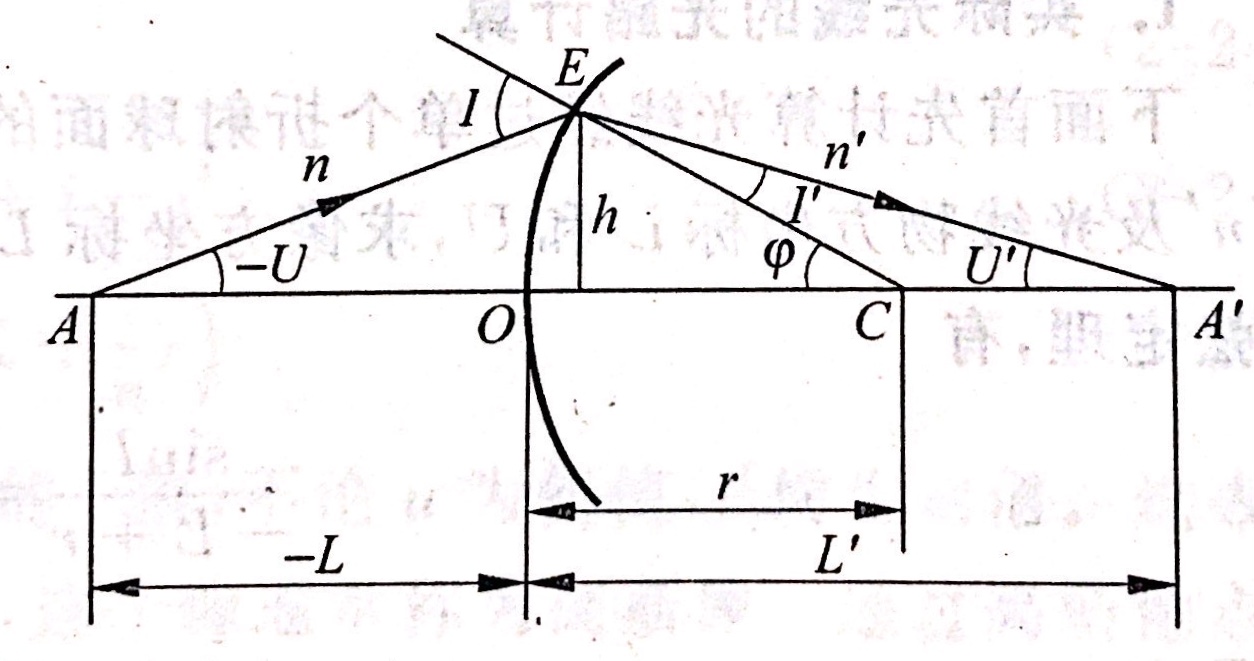
- 物方截距:顶点 O O O到光线与光轴交点 A A A的距离 L = O A L=OA L=OA;
- 物方孔径角:入射光线与光轴的夹角
U
=
∠
O
A
E
U=\angle OAE
U=∠OAE
与物方对应,光线经折射面 O E OE OE折射后,与光轴相交于 A ′ A^{'} A′点,像方也有像方截距 O A ′ OA^{'} OA′和像方孔径角 ∠ O A ′ E \angle OA^{'}E ∠OA′E。另外要注意,在进行光路分析时,需要有一套规定好的符号规则来确定其中各参数的负号正负关系,并在运用过程中始终遵循这样一套规则,保证分析和设计的正确性。
2、单一球面透镜及薄透镜成像
(1)单一球面透镜成像
以上图为例推导单一球面的光路,已知物方各参数以及折射率和球面半径求像方截距和像方孔径角。在
Δ
A
E
C
\Delta AEC
ΔAEC和
Δ
A
′
E
C
\Delta A^{'}EC
ΔA′EC中应用正弦定理和
E
E
E点折射定律,可以得出:
s
i
n
I
−
L
+
r
=
s
i
n
(
−
U
)
r
\frac{sinI}{-L+r}=\frac{sin(-U)}{r}
−L+rsinI=rsin(−U)
s
i
n
I
′
L
′
−
r
=
s
i
n
U
′
r
\frac{sinI^{'}}{L^{'}-r}=\frac{sinU^{'}}{r}
L′−rsinI′=rsinU′
s
i
n
I
′
=
n
n
′
s
i
n
I
sinI^{'}=\frac{n}{n^{'}}sinI
sinI′=n′nsinI
结合几何关系,联立后即可得到像方截距和像方孔径角分别为:
U
′
=
U
+
I
−
I
′
U^{'}=U+I-I^{'}
U′=U+I−I′
L
′
=
r
(
1
+
s
i
n
I
′
s
i
n
U
′
)
L^{'}=r(1+\frac{sinI^{'}}{sinU^{'}})
L′=r(1+sinU′sinI′)
由上式可以看出,以
A
A
A为顶点
2
U
2U
2U为顶角的圆锥面上的光线经过球面折射后都会汇聚于
A
′
A^{'}
A′点上,但是由于
L
′
L^{'}
L′是
U
U
U的函数,当物方截距
L
L
L固定而物方孔径角
U
U
U变化时,即同一物点发出的不同孔径角的光经折射后会汇聚在不同像方截距
L
′
L^{'}
L′处,这表面单一球面对轴上物点的成像不是完善的,存在“球差”。
当光线在光轴附近很小区域内时称为近轴光线,对应的孔径角也很小,所以,将角度的正弦值用弧度来代替,可以发现在近轴区内对于给定的
l
l
l,对应的
l
′
l^{'}
l′均为定值,与
u
u
u无关,表明近轴区内细光束的成像是完善的,这个像称为 高斯像,构成这一物像关系的两点称为共轭点。可以进一步推出近轴区单一折射球面的光线成像公式,
Q
Q
Q为阿贝不变量,
Φ
\Phi
Φ为光焦度:
n
′
(
1
r
−
1
l
′
)
=
n
(
1
r
−
1
l
)
=
Q
n^{'}(\frac{1}{r}-\frac{1}{l^{'}})=n(\frac{1}{r}-\frac{1}{l})=Q
n′(r1−l′1)=n(r1−l1)=Q
n
′
u
′
−
n
u
=
(
n
′
−
n
)
h
r
n^{'}u^{'}-nu=(n^{'}-n)\frac{h}{r}
n′u′−nu=(n′−n)rh
n
′
l
′
−
n
l
=
n
′
−
n
r
=
Φ
\frac{n^{'}}{l^{'}}-\frac{n}{l}=\frac{n^{'}-n}{r}=\Phi
l′n′−ln=rn′−n=Φ
总结: 对于一个有 k k k个面组成的光学系统,其成像特性由以下结构参数确定:
- 各球面的曲率半径;
- 相邻球面顶点的间隔;
- 各面之间介质的折射率;
(2)薄透镜成像
薄透镜由两个折射球面组成,两面的间距为
d
d
d(
d
d
d<<球面曲率半径
r
r
r),在计算中可以忽略。物点
A
A
A经经第一折射球面成像于
A
′
A^{'}
A′,再经第二折射球面成像于
A
′
′
A^{''}
A′′。
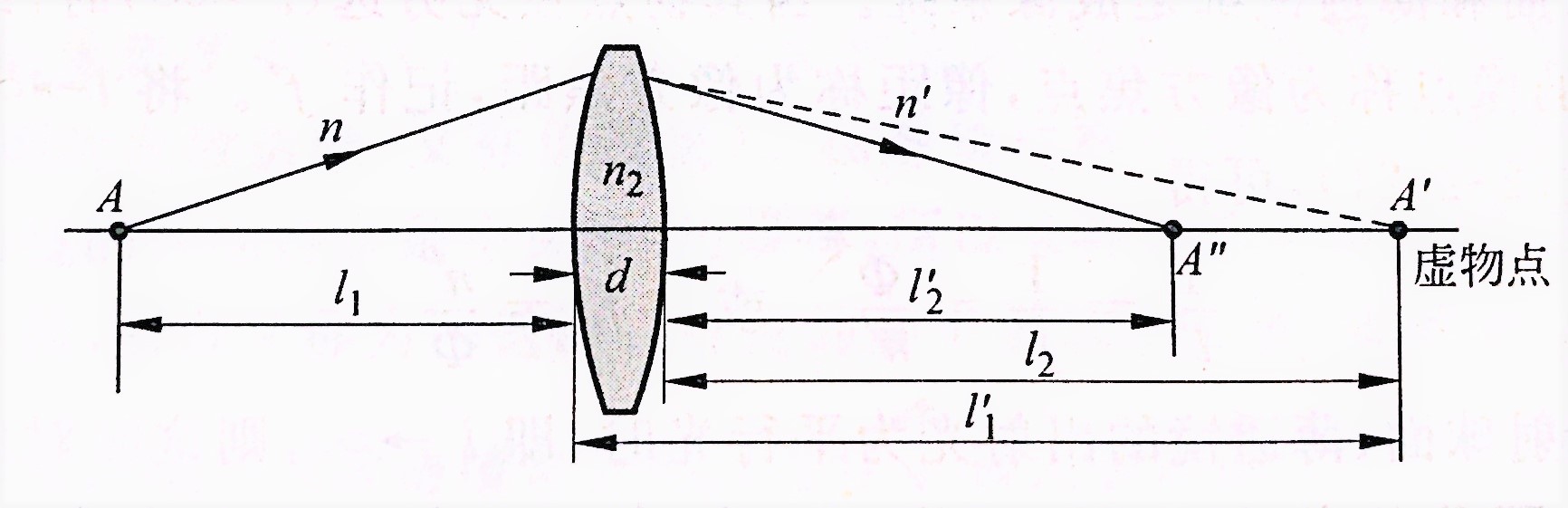
根据上面推出的近轴区折射球面的光线成像公式,可以得到薄透镜的成像公式(
Φ
\Phi
Φ为薄透镜的光焦度):
n
′
l
′
−
n
l
=
n
2
−
n
r
1
+
n
′
−
n
2
r
2
=
Φ
1
+
Φ
2
=
Φ
\frac{n^{'}}{l^{'}}-\frac{n}{l}=\frac{n_2-n}{r_1}+\frac{n^{'}-n_2}{r_2}=\Phi_1+\Phi_2=\Phi
l′n′−ln=r1n2−n+r2n′−n2=Φ1+Φ2=Φ
当物点在无穷远处时,即以平行光入射时,对应的像点称为像方焦点,像距称为像方焦距
f
′
f^{'}
f′。相反,出射光为平行光时对应的物点称为物方焦点,物距称为物方焦距
f
f
f。单一折射折射球面近轴区和薄透镜的焦距公式可将
l
l
l令为无穷大带入上式中得到:
f
′
=
n
′
Φ
f^{'}=\frac{n^{'}}{\Phi}
f′=Φn′
f
=
−
n
Φ
f=-\frac{n}{\Phi}
f=−Φn
薄透镜的光焦度大于0时,则为会聚透镜,光焦度小于0时为发散透镜。当透镜在空气(同一介质)当中时,物方焦距于像方焦距大小相等,符号相反。将这两式子带入上面的薄透镜的成像公式,可以得到透镜成像公式的高斯形式:
f
′
l
′
+
f
l
=
1
\frac{f^{'}}{l^{'}}+\frac{f}{l}=1
l′f′+lf=1
3、光阑
(1)孔径光阑
决定着从物面通过光学系统能到达其像面或聚光面的光束横截面大小(注意“到达”二字,与下面的视场光阑重点区分)的元件即为 孔径光阑(如:照相机镜头的光圈)。进一步根据孔径光阑在光学系统中的位置将其分为孔阑入瞳和孔阑出瞳,如下图所示。
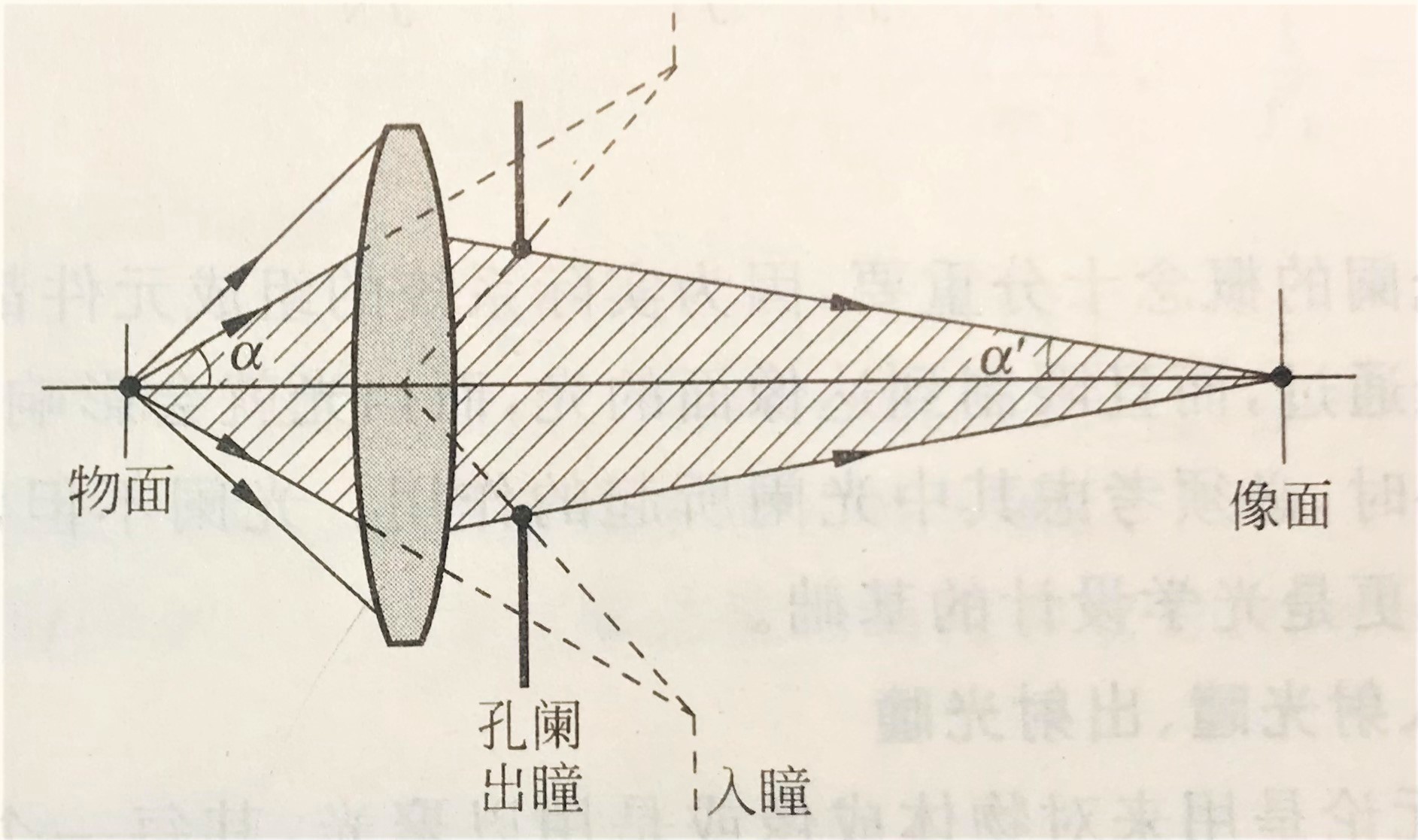
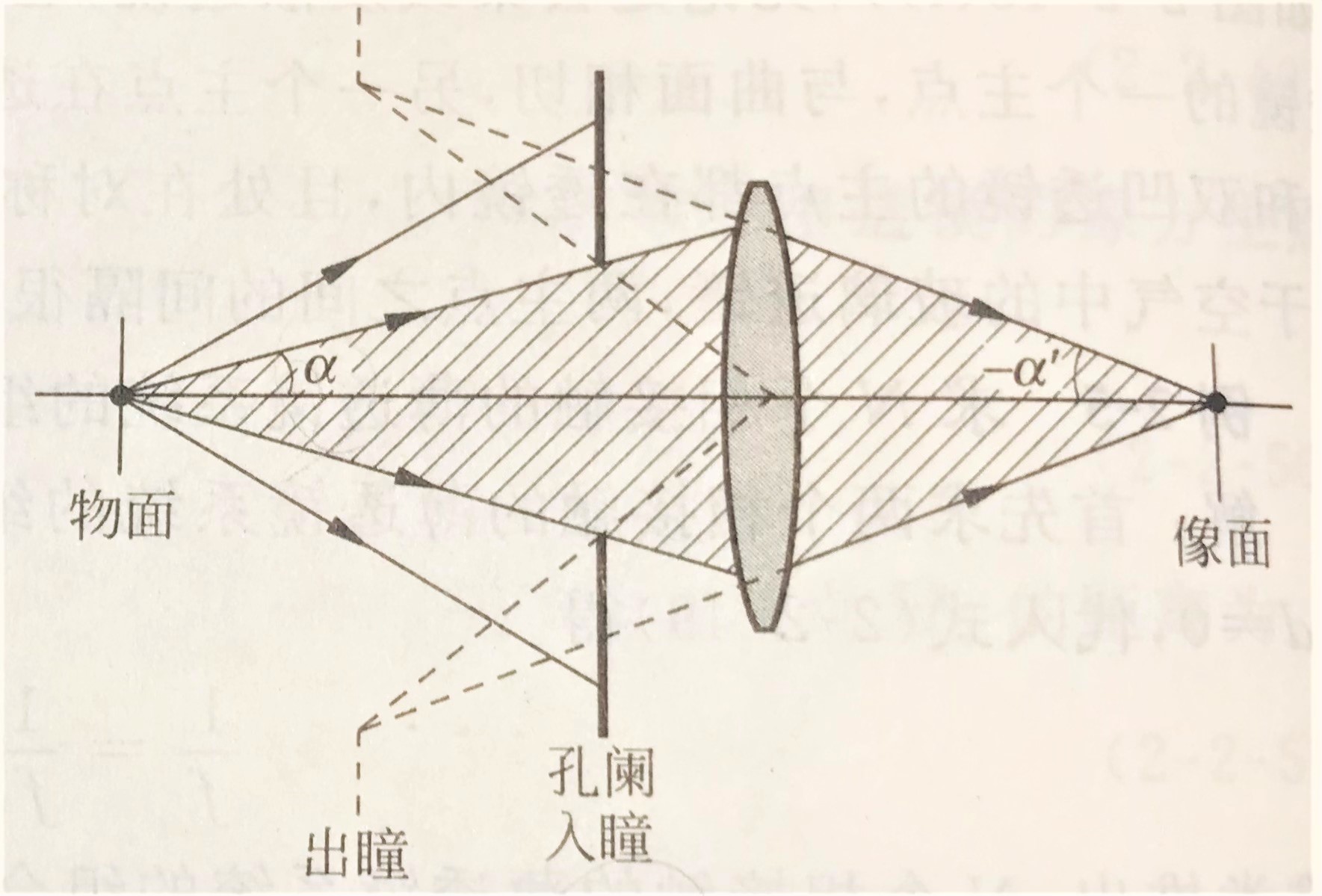
在此基础上,引入相对孔径和 f f f数的概念:相对孔径为系统入瞳直径 D D D与系统像方焦距 f ′ f^{'} f′的比值,而 f f f数为系统相对孔径的倒数(记为: f f f/n),即
f
/
n
=
f
′
D
f/n=\frac{f^{'}}{D}
f/n=Df′
照相机的曝光时间正比于其
f
f
f数的平方,
f
f
f数越大,则曝光时间越长。
(2)视场光阑
决定着光学系统像面或聚光面大小的元件即为 视场光阑。如下图所示,定义从某物点发出的经过入瞳中心的光线为此物点的主光线。当轴外物点离光轴的距离增加时,其主光线最终会与某一元件的边缘相交,这一元件即为视场光阑。视场光阑被前方系统所成的像称为入射窗,被后方系统所成的像称为出射窗。
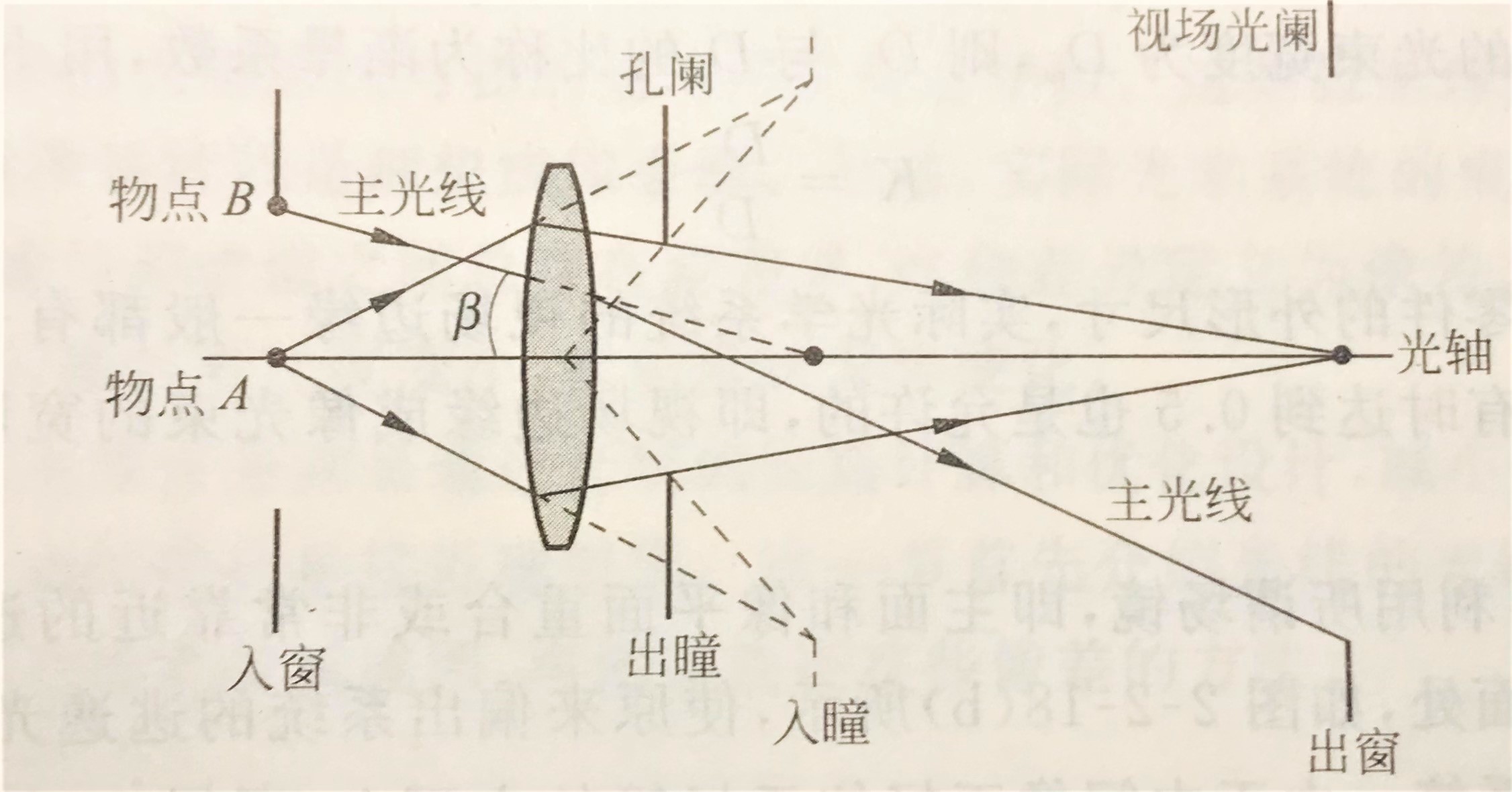
通过上面分析,我们可以知道视场光阑限制了最边缘物点的主光线的通过,但还是会有更边缘物点的部分光通过,另外对于主光线能正常通过的不同位置处的物点也会有不同程度的光束无法通过。因此,就导致像面上各点光强不均匀的现象,即渐晕现象。利用主面和像平面位置非常接近的透镜(即场镜)可以减少渐晕。
三、光学设计及光学材料
1、光学设计
光学设计的主要任务是通过光线光路的计算和优化设计,减小光学系统的像差,使实际光学系统所成的像尽量接近理想的像。按理说从物点发出进入光学系统并成像的光线有无数条,故不可能对每一条光线都进行光路计算。一般来说,对于实际的光学系统,已知其结构参数、物体大小位置和孔径光阑的大小位置,需要进行以下光线的计算:
- 计算近轴光线求理想像的位置和大小;
- 计算子午面内实际光线光路,求实际像的位置大小及有关像差;
- 计算轴外点沿主光线的细光束光路求细光束的像散和场曲;
- 子午面外的空间光线光路计算,求空间光线的子午像差分量和弧矢像差分量。
随着光学系统的设计指标不断提高,光线光路计算一般要通过相应的CAD软件进行设计,目前国际上常用的有美国Focus Software公司研制的 ZEMAX 等(之后准备写一篇该软件的基本使用教程)。在时间较急的情况下,建议读者可以考虑直接入手该软件进行光学设计,省去利用公式用手计算的步骤。讲到光学设计,就有必要了解一下像差理论,像差可分为单色像差和色差两大类,其中单色像差包括:球差、慧差、像散、场曲和畸变。
1)球差:像差在第二节的单一球面透镜成像中涉及过,它指的是主光轴上一物点发出的光束,经过光学系统(如凸透镜)后不再交于一点,近轴光线交于较远处,而边缘光线交于较近处(正球差),若将一个屏幕放在成像处将观察到一个弥散斑,这一现象被称为球差。对于单个透镜而言,可以证明当透镜的曲率(同样焦距的透镜曲率比可以不同)比为:
r
1
r
2
=
−
4
+
n
−
2
n
2
n
(
1
+
2
n
)
\frac{r_1}{r_2}=-\frac{4+n-2n^2}{n(1+2n)}
r2r1=−n(1+2n)4+n−2n2
时,球差最小,上式被称为最小球差条件,这种减小球差的方法称为配曲法。
2)彗差:球差针对的是主光轴上的物点,但近轴物点经过系统后也依旧无法相较于一点,而是在理想平面上形成如彗星的亮斑,也因此这种像差被称为慧差。在显微镜成像时,由于物距很短,因此必须要想办法消除球差和慧差。
3)畸变:球差、慧差、像散和场曲一般只会影响成像的清晰度,而由于光束倾斜导致离轴距离不同的各点垂轴放大率不同,进而使得像与原物在形状上失真,这种影响成像形状的像差被称为畸变。放大率随离轴距离的增大而增大的畸变为正畸变(光阑位于透镜之前),反之为负畸变(光阑位于透镜后面)。
4)色差:由于光学材料的折射率与光波长有关,故光学系统的焦距也和波长有关,不同颜色的光所成的像,其位置和大小都可能不同,与位置有关的称为轴向色差,与大小有关的称为横向色差。轴向色差和横向色差通常用氢光谱中的C、F、D线对应的像距和像高之差来表示。可以选用两种不同材料的胶合透镜来对两种选定的波长消除色差。
2、光学玻璃
光学玻璃是最常用的光学材料,与普通玻璃相比,光学玻璃具有以下特点:高度的透明性、高度的均匀性、好的化学稳定性以及特定的光学常数。大多数光学玻璃以二氧化硅为主要成分(硅酸盐玻璃),其次是以氧化硼为主的硼酸盐玻璃。光学材料的折射特性一般用夫琅禾费特征谱线的折射率和色散系数来表示。
1)无色光学玻璃
无色光学玻璃按光学常数可分为:冕牌玻璃和火石玻璃。冕牌玻璃折射率较低(
n
D
n_D
nD=1.50~1.55),色散小(
ν
D
=
\nu_D=
νD= 55~62),而火石玻璃折射率高 (
n
D
n_D
nD=1.53~1.85),色散小(
ν
D
\nu_D
νD =30~45)。在制造要求较高的光学仪器时需要重点考虑的指标有:
- 折射率、色散系数的允差及一致性:目视仪器的常规光学玻璃以D光、F光和C光的折射率为主要特征,这是因为C、F光位于人眼敏感区两端,而D光位于其中接近人眼最敏感的谱线。
- 光学均匀性:同一玻璃中各部分折射率变化的不均匀程度;
- 应力双折射:存在内应力的光学玻璃破坏了各向同性,会发生双折射现象;
- 光吸收系数:1cm厚光学玻璃吸收白光的光通量与进入玻璃的白光光通量之比;
- 条纹度和气泡度:条纹是玻璃内部的局部缺陷,气泡是玻璃熔融过程中气体来不及溢出所致,它们的存在会导致光的散射和折射。
2)有色光学玻璃
有色光学玻璃是在无色光学玻璃的成分中加入少量着色剂制成,用以改变光强或光谱成分,提高光学仪器的能见度。有色光学玻璃可分为:选择吸收玻璃(吸收特定波段的光谱,曲线2),中性玻璃(在可见光范围内较均匀地降低透射光强度,曲线1)和晒镉玻璃(有较宽的高透过区和高吸收区,曲线3)。
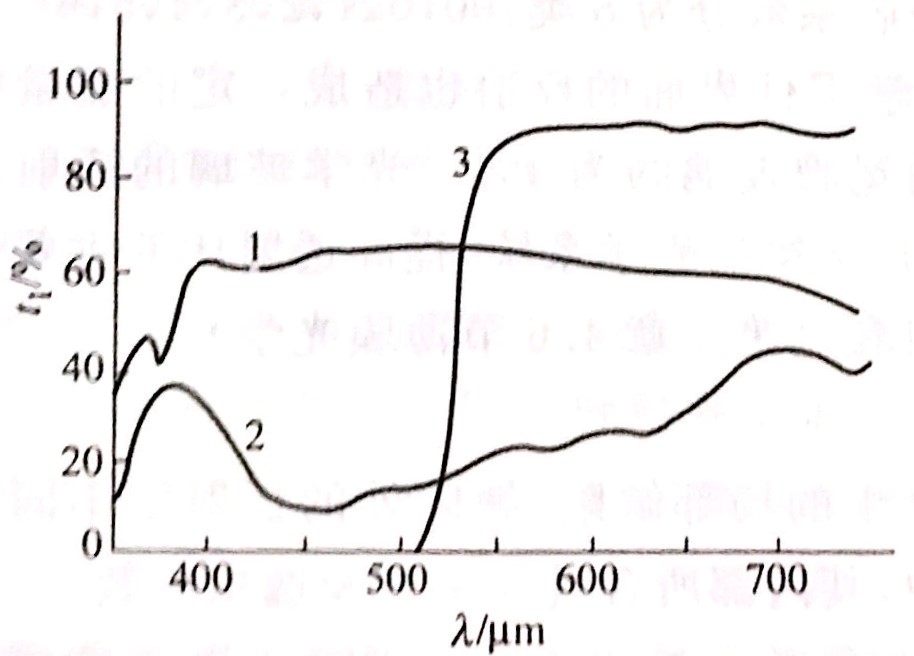
3)特种光学玻璃
随着仪器使用范围的扩大,对光学玻璃提出了许多特殊的要求,特种光学玻璃的品类也在逐渐增加,如:光学石英玻璃、红外光学玻璃、耐辐射光学玻璃和防辐射光学玻璃、微晶玻璃(热膨胀系数极低)。








 本文介绍了物理光学的基础,包括光的电磁理论、几何光学原理、成像方法和光学设计。讨论了光的直线传播定律、反射定律、折射定律以及费马原理。详细阐述了单一球面透镜和薄透镜的成像公式,解释了像差的概念,如球差、慧差、像散和畸变,并提到了光学材料如光学玻璃的选择。此外,还涉及了光学设计中的像差校正和光学系统的优化。
本文介绍了物理光学的基础,包括光的电磁理论、几何光学原理、成像方法和光学设计。讨论了光的直线传播定律、反射定律、折射定律以及费马原理。详细阐述了单一球面透镜和薄透镜的成像公式,解释了像差的概念,如球差、慧差、像散和畸变,并提到了光学材料如光学玻璃的选择。此外,还涉及了光学设计中的像差校正和光学系统的优化。

















 2914
2914

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










