在看论文过程中,常常会遇到一些文章对gnss观测方程进行了参数重整,获得新的有偏参数,如何判断这些新参数是否可估呢?
判断参数可估性并在不可估(即设计矩阵秩亏)时给出参数重整方案,Teunissen在1985年将S变换理论应用到了gnss领域,用于解决上述问题。
S变换理论的核心思想为:有一个观测方程,其中y为观测值,维度m*1;x为待估参数,维度n*1;A为设计矩阵,维度m*n,m>n。当
时,矩阵秩亏,无法估得无偏参数,只有进行参数重整,减少待估参数数量(可估参数数量为A的秩,即r)才可进行求解。
这里回顾线性代数中矩阵的子空间,已知,零空间
;列空间
;行空间
;左零空间
。如何利用这些子空间获得可估参数的形式呢?
由于参数无法无偏估计得到,我们将
拆分为可估参数
(r*1)和不可估参数
((n-r)*1),即
,其中V维度(n-r)*1,即A的零空间,满足
;S维度n*r,为V的补空间,带入原式
,构成了新的观测方程。参数重整的目的就是获得可估参数
但这里存在的难点是补空间S不是唯一的,如何获得简单的S从而得到简洁的可估参数形式笔者觉得需要技巧。
例子:



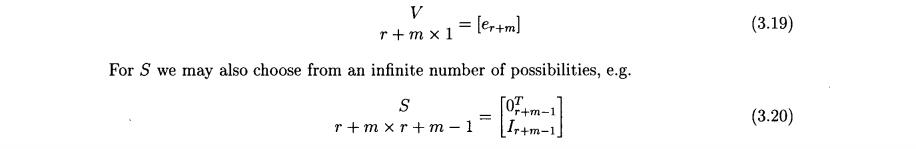






















 830
830











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








