【论文笔记】 VIT论文笔记，重构Patch Embedding和Attention部分

0 前言

相关链接：

1. VIT论文：https://arxiv.org/abs/2010.11929
2. VIT视频讲解：https://www.bilibili.com/video/BV15P4y137jb/?spm_id_from=333.999.0.0&vd_source=fff489d443210a81a8f273d768e44c30
3. VIT源码：https://github.com/vitejs/vite
4. VIT源码(Pytorch版本，非官方，挺多stars，应该问题不大)：https://github.com/lucidrains/vit-pytorch

重点掌握：

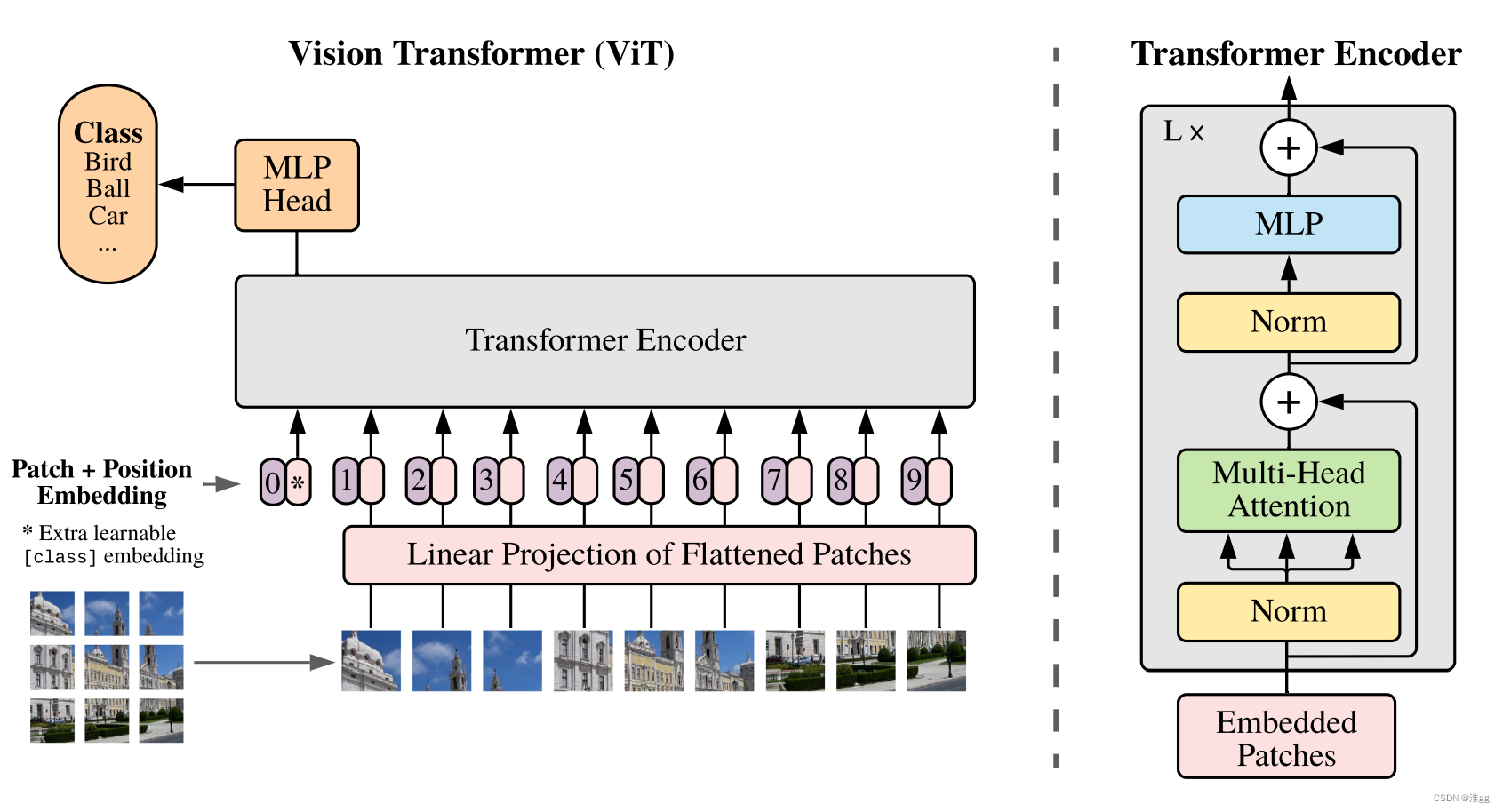
5. 如何将2-D的图像变为1-D的序列，操作：PatchEmbedding，并且加上learnbale embedding 和 Position Embedding
6. Multi-Head Attention的写法，其中里面有2个Linear层进行维度变换~

VIT历史意义： 展示了在CV中使用纯Transformer结构的可能，并开启了视觉Transformer研究热潮。

1 总体代码

说明： 本文代码是针对VIT的Pytorch版本进行重构修改，若有不对的地方，欢迎交流~
原因： lucidrains的源码中调用了比较高级的封装，如einops包中的rerange等函数，写的确实挺好的，但不好理解shape的变化；

import torch
import torch.nn as nn

class PatchAndPosEmbedding(nn.Module):
    def __init__(self, img_size=256, patch_size=32, in_channels=3, embed_dim=1024, drop_out=0.):
        super(PatchAndPosEmbedding, self).__init__()

        num_patches = int((img_size/patch_size)**2)
        patch_size_dim = patch_size*patch_size*in_channels

        # patch_embedding, Note: kernel_size, stride
        # a
        self.patch_embedding = nn.Conv2d(in_channels=in_channels, out_channels=patch_size_dim, kernel_size=patch_size, stride=patch_size)
        self.linear = nn.Linear(patch_size_dim, embed_dim)

        self.cls_token = nn.Parameter(torch.randn(1, 1, embed_dim))   # 添加一个cls_token用于整合信息
        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches+1, embed_dim)) # 给patch embedding加上位置信息

        self.dropout = nn.Dropout(drop_out)

    def forward(self, img):
        x = self.patch_embedding(img) # [B,C,H,W] -> [B, patch_size_dim, N, N] # N = Num_patches = (H*W)/Patch_size,
        x = x.flatten(2)
        x = x.transpose(2, 1)  # [B,N*N, patch_size_dim]
        x = self.linear(x)     # [B,N*N, embed_dim]  # patch_size_dim -> embed_dim = 3072->1024 to reduce the computation when encode.

        cls_token = self.cls_token.expand(x.shape[0], -1, -1)  # cls_token: [1,1 embed_dim] -> [B, 1, embed_dim]
        x = torch.cat([cls_token, x], dim=1) # [B,N*N, embed_dim] -> [B, N*N+1, embed_dim]
        x += self.pos_embedding  # [B, N*N+1, embed_dim]  Consider why not concat , but add?  Trade off due to the computation.

        out = self.dropout(x)

        return out

class Attention(nn.Module):
    def __init__(self, dim, heads=16, head_dim=64, dropout=0.):
        super(Attention, self).__init__()
        inner_dim = heads * head_dim  # 可以通过FC将 input_dim 映射到inner_dim作为注意力表示维度
        self.heads = heads
        self.scale = head_dim ** -0.5

        project_out = not (heads == 1 and head_dim == dim)

        # 构建 k,q,v，可根据VIT原项目中的rerange进行变化
        # 写法一：直接定义to_q, to_k, to_v
        self.to_q = nn.Linear(dim, inner_dim, bias = False)
        self.to_k = nn.Linear(dim, inner_dim, bias = False)
        self.to_v = nn.Linear(dim, inner_dim, bias = False)

        # 写法二：先定义qkv，在forward进行chunk拆开
        # self.to_qkv = nn.Linear(dim, inner_dim*3, bias = False)

        self.atten = nn.Softmax(dim=-1)
        self.dropout = nn.Dropout(dropout)

        self.to_out = nn.Sequential(nn.Linear(dim, inner_dim), nn.Dropout(dropout)) if project_out else nn.Identity()

    def forward(self, x):
        # 续上面写法1：
        q = self.to_q(x)  # [3,65,1024]
        k = self.to_k(x)  # [3,65,1024]
        v = self.to_v(x)  # [3,65,1024]

        # 续上面写法2：
        # toqkv = self.to_qkv(x)  # [3, 65, 3072]
        # q, k, v = toqkv.chunk(3, dim=-1)  # q, k, v.shape    [3,65,1024]

        q = q.reshape(q.shape[0], q.shape[1], self.heads, -1).transpose(1, 2)  # [3,65,1024]  -> [3,16,65,64]
        k = k.reshape(k.shape[0], k.shape[1], self.heads, -1).transpose(1, 2)  # [3,65,1024]  -> [3,16,65,64]
        v = v.reshape(v.shape[0], v.shape[1], self.heads, -1).transpose(1, 2)  # [3,65,1024]  -> [3,16,65,64]


        dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale

        atten = self.atten(dots)
        atten = self.dropout(atten)

        out = torch.matmul(atten, v)    # [3, 16, 65, 64]
        out = out.transpose(1, 2)   #
        out = out.reshape(out.shape[0], out.shape[1], -1)   # [3, 65, 16*64]

        return self.to_out(out)

class MLP(nn.Module):  # 搭建2层FC， 使用GELU激活
    def __init__(self, dim, hidden_dim, dropout=0.):
        super(MLP, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(dim, hidden_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(hidden_dim, dim),
            nn.GELU(),
            nn.Dropout(dropout)
        )

    def forward(self, x):
        return self.net(x)

class PreNorm(nn.Module):  # Encoder结构中先LayerNorm再进行Multihead-attention或MLP
    def __init__(self, dim, fn):
        super(PreNorm, self).__init__()
        self.norm = nn.LayerNorm(dim)
        self.fn = fn
    def forward(self, x, **kwargs):
        return self.fn(self.norm(x), **kwargs)

class Transformer(nn.Module):  # 整个Encoder结构
    def __init__(self, dim, depth, heads, head_dim, mlp_hidden_dim, dropout=0.):
        super(Transformer, self).__init__()
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(
                nn.ModuleList([
                    PreNorm(dim, Attention(dim, heads, head_dim, dropout=dropout)),
                    PreNorm(dim, MLP(dim, mlp_hidden_dim, dropout=dropout))
                ]))

    def forward(self, x):
        for attn, ff in self.layers:
            x = attn(x) + x
            x = ff(x) + x
        return x

class VIT(nn.Module):
    def __init__(self, num_classes=10, img_size=256, patch_size=32, in_channels=3,
                 embed_dim=1024, depth=6, heads=16, head_dim=64, mlp_hidden_dim=2048, pool='cls', dropout=0.1):
        super(VIT, self).__init__()

        assert pool in {'cls', 'mean'}, 'pool type must be either cls (cls token) or mean (mean pooling)'
        self.pool = pool

        self.patchembedding = PatchAndPosEmbedding(img_size, patch_size, in_channels, embed_dim, dropout)

        self.transformer = Transformer(embed_dim, depth, heads, head_dim, mlp_hidden_dim, dropout)

        self.to_latent = nn.Identity()

        self.mlp_head = nn.Sequential(
            nn.LayerNorm(embed_dim),
            nn.Linear(embed_dim, num_classes)
        )
    def forward(self, x):
        x = self.patchembedding(x)
        x = self.transformer(x)

        x = x.mean(dim=1) if self.pool == 'mean' else x[:, 0]

        out = self.mlp_head(x)

        return out


net = VIT()
x = torch.randn(3, 3, 256, 256)
out = net(x)
print(out, out.shape)

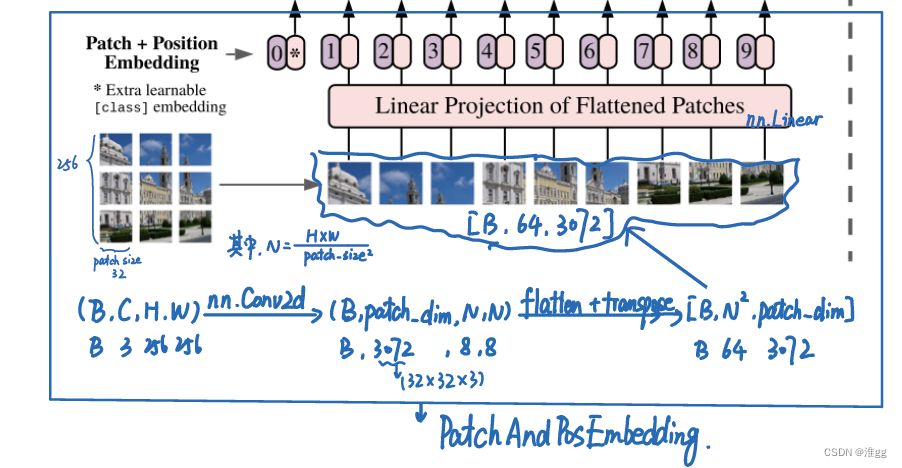
2 PatchandPosEmbedding

说明：
1.将256x256x3的图像分为32x32x3大小的patches，主要使用nn.Conv2d实现，主要是ernel_size==patch_size 和stride==patch_size， 多看代码就能理解这个图了；
2.由于图像切分重排后失去了位置信息，并且Transformer的运算是与空间位置无关的，因此需要把位置信息编码放进网络，使用一个向量进行编码，即PosEmbedding；

问题：
1. 为什么要在Embedding时加上一个patch0，即代码中的cls_tocken？
原因：假设原始输出的9个向量（以图中假设），若随机选择其中一个用于分类，效果都不好。若全用的话，计算量太大；因此加上一个可学习的向量，即learnable embedding用于整合信息。
2.为什么Position Embedding是直接add，而不是concat？
原因：实际上add是concat的一种特例，而concat容易造成维度太大导致计算量爆炸，实际上，该部分的add是对计算量的一种妥协，但在论文中的Appendix部分可以看出，这种方法的定位效果还是不错的。

class PatchAndPosEmbedding(nn.Module):
    def __init__(self, img_size=256, patch_size=32, in_channels=3, embed_dim=1024, drop_out=0.):
        super(PatchAndPosEmbedding, self).__init__()

        num_patches = int((img_size/patch_size)**2)
        patch_size_dim = patch_size*patch_size*in_channels

        # patch_embedding, Note: kernel_size, stride
        # a
        self.patch_embedding = nn.Conv2d(in_channels=in_channels, out_channels=patch_size_dim, kernel_size=patch_size, stride=patch_size)
        self.linear = nn.Linear(patch_size_dim, embed_dim)

        self.cls_token = nn.Parameter(torch.randn(1, 1, embed_dim))   # 添加一个cls_token用于整合信息
        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches+1, embed_dim)) # 给patch embedding加上位置信息

        self.dropout = nn.Dropout(drop_out)

    def forward(self, img):
        x = self.patch_embedding(img) # [B,C,H,W] -> [B, patch_size_dim, N, N] # N = Num_patches = (H*W)/Patch_size,
        x = x.flatten(2)
        x = x.transpose(2, 1)  # [B,N*N, patch_size_dim]
        x = self.linear(x)     # [B,N*N, embed_dim]  # patch_size_dim -> embed_dim = 3072->1024 to reduce the computation when encode.

        cls_token = self.cls_token.expand(x.shape[0], -1, -1)  # cls_token: [1,1 embed_dim] -> [B, 1, embed_dim]
        x = torch.cat([cls_token, x], dim=1) # [B,N*N, embed_dim] -> [B, N*N+1, embed_dim]
        x += self.pos_embedding  # [B, N*N+1, embed_dim]  Consider why not concat , but add?  Trade off due to the computation.

        out = self.dropout(x)

        return out

3. Attention

实现Attention机制，需要Q(Query),K(Key),V(Value)三个元素对注意力进行计算，实际上是对各个patches之间计算注意力值，公式为

class Attention(nn.Module):
    def __init__(self, dim, heads=16, head_dim=64, dropout=0.):
        super(Attention, self).__init__()
        inner_dim = heads * head_dim  # 可以通过FC将 input_dim 映射到inner_dim作为注意力表示维度
        self.heads = heads
        self.scale = head_dim ** -0.5

        project_out = not (heads == 1 and head_dim == dim)

        # 构建 k,q,v，可根据VIT原项目中的rerange进行变化
        # 写法一：直接定义to_q, to_k, to_v
        self.to_q = nn.Linear(dim, inner_dim, bias = False)
        self.to_k = nn.Linear(dim, inner_dim, bias = False)
        self.to_v = nn.Linear(dim, inner_dim, bias = False)

        # 写法二：先定义qkv，在forward进行chunk拆开
        # self.to_qkv = nn.Linear(dim, inner_dim*3, bias = False)

        self.atten = nn.Softmax(dim=-1)
        self.dropout = nn.Dropout(dropout)

        self.to_out = nn.Sequential(nn.Linear(dim, inner_dim), nn.Dropout(dropout)) if project_out else nn.Identity()

    def forward(self, x):
        # 续上面写法1：
        q = self.to_q(x)  # [3,65,1024]
        k = self.to_k(x)  # [3,65,1024]
        v = self.to_v(x)  # [3,65,1024]

        # 续上面写法2：
        # toqkv = self.to_qkv(x)  # [3, 65, 3072]
        # q, k, v = toqkv.chunk(3, dim=-1)  # q, k, v.shape    [3,65,1024]

        q = q.reshape(q.shape[0], q.shape[1], self.heads, -1).transpose(1, 2)  # [3,65,1024]  -> [3,16,65,64]
        k = k.reshape(k.shape[0], k.shape[1], self.heads, -1).transpose(1, 2)  # [3,65,1024]  -> [3,16,65,64]
        v = v.reshape(v.shape[0], v.shape[1], self.heads, -1).transpose(1, 2)  # [3,65,1024]  -> [3,16,65,64]


        dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale

        atten = self.atten(dots)
        atten = self.dropout(atten)

        out = torch.matmul(atten, v)    # [3, 16, 65, 64]
        out = out.transpose(1, 2)   #
        out = out.reshape(out.shape[0], out.shape[1], -1)   # [3, 65, 16*64]

        return self.to_out(out)