布尔定理及证明（完整版）

这篇文章的目的是以布尔代数公理证明定理。

对偶原理：0with1,+ with · 互换以后，公理（定理）任然成立。

布尔代数的公理如下

单变量的布尔代数定理如下

单变量的布尔代数定理很容易用真值表证明。

多变量的布尔定理如下

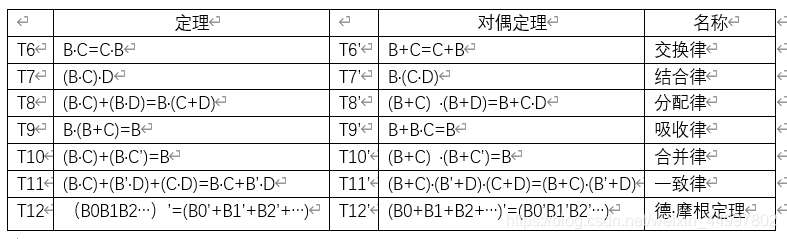
交换律，结合律，分配律同样容易用真值表证明。其中T8’最好用对偶法则记忆。

吸收律的证明需要用到分配律：
B·(B+C)=(B+B)·(B+C)=B+B·C=B·1+B·C=B·(1+C)=B·1=B 证毕

合并律也很容易用分配律证得，不再赘述。

一致律的一种证明方式是展开：
B·C+B’·D+C·D
=B·C·(D+D’)+B’·(C+C’)·D+(B+B’)·C·D
=BCD+BCD’+B’CD+B’C’D+BCD+B’CD
(容易发现第5项和第1项重复，第6项和第3项重复，根据重叠定理可以消去)
= BCD+BCD’+B’CD+B’C’D
= B·C+B’·D

一种证明方式是添项：
(B+C)(B’+D)(C+D)
=(B+C) (C+D) (B’+D)(C+D)
=(C+BD)(D+B’C)
=CD+BD+B’C
=CD+BD+B’C+B’B
=(B+C)D+(B+C)B’
=(B+C)(B’+D)