Python实现时间序列中的ARIMA模型(学习笔记)

最新推荐文章于 2024-01-27 10:56:59 发布

HarvestII

最新推荐文章于 2024-01-27 10:56:59 发布

阅读量2.8k

点赞数 3

分类专栏： python

本文链接：https://blog.csdn.net/weixin_45008173/article/details/107469022

版权

python 专栏收录该内容

9 篇文章 3 订阅

订阅专栏

文章目录

本篇文章仅为学习笔记，阅读本文章您很难获得收获。😊

ARIMA模型

ARIMA模型其实就是3个模块的缩写:AR(自回归模型)、I(整合)、MA(移动平均模型)。

AR

AR自回归模型描述的是当前值和历史值之间的一个关系，用变量自身的历史数据对未来进行预测，这个AR模型必须是平稳的才能使用，平稳通俗来说就是变化在上下某个区间内浮动(后面的图会解释)，如果不平稳，我们可以通过差分的方法使得数据变得平稳。然后再通过一定的关系来进行数据的预测。
回归模型中用来描述当前数据和历史数据的关系的方程如下： $y_t = \mu+\sum\limits_{i=1}^p\gamma_iy_{t-i}+\epsilon_t$
其中 $y_t$ 表示当前数据， $\mu$ 是常数项， $p$ 是一个阶数，表示的是用t前多少个单位的数据来分析 $y_t$ ， $\epsilon_t$ 表示的是误差。
自回归模型在使用时要注意：

自回归模型使用的数据必须是和要预测数据
要求数据与时间的关系，即相关系数必须大于0.5，否则预测则不准确。
数据必须具有平稳性，不平稳则必须进行前期处理。

MA模型

MA模型即移动平均模型，移动平均模型的主要作用就是为了消除图像的误差，大致思路就是用误差来消除误差并表示目标变量的思路。模型方程如下：
$y_t = \mu+\epsilon_t +\sum\limits_{i=1}^q\theta_i\epsilon_{t-i}$
其中q表示与前面p的含义一致，都是为了表示用前面的q个误差。

ARMA模型

将两者结合在一起形成的。
$y_t= \mu+\sum\limits_{i=1}^p\gamma_iy_{t-i}+\epsilon_t +\sum\limits_{i=1}^q\theta_i\epsilon_{t-i}$

基本步骤

首先应当对数据进行平稳性检验，已确定数据符合平稳性，若不符合则要进行差分。

平稳检验

检验数据平稳的方法，常规上使用ADF检验法来进行检验，验证是否满足ADF检验的结果。数学原理这里不再阐释(ADF算法)，说明一下python中的方法的参数。

statsmodels.tsa.stattools.adfuller(x, maxlag=None, regression='c', autolag='AIC', store=False, regresults=False)

这个方法是在statsmodels模块中的一个方法，在使用时注意引入对应的package。

x指的是，需要进行检测的数列，
maxlag指的是最大的滞后参数，应该是个整数，如果不设置就是当前数列的长度。
autolag这个指的是自动确定滞后参数的方法，这个我也不懂怎么确定的，默认使用的是AIC 详细解释传送门

返回值还是挺重要的，这个东西实我们判断是否稳定的依据：
返回值:

p值，和假设检验里面的一样
adf统计值，根据前面设定的p值算出的adf统计值，这个主要作用是和后面的一些数值进行对比用的。
uselag，表示的是使用的滞后系数
critical values，表示的是一个根据当前数据所对应的参考值，是一个字典，字典的key是参考p值，value是参考p值对应的adf统计值。根据我们得到的实际的p值和实际的adf值与参考值进行对比可以判断，我们的数据是否是平稳的。

举个例子：

# ADF test on random numbers
series = np.random.randn(100)
result = adfuller(series, autolag='AIC')
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')
for key, value in result[4].items():
    print('Critial Values:')
    print(f'   {key}, {value}')

结果：

ADF Statistic: -7.4715740767231456
p-value: 5.0386184272419386e-11
Critial Values:
   1%, -3.4996365338407074
Critial Values:
   5%, -2.8918307730370025
Critial Values:
   10%, -2.5829283377617176

对比参考数据和实际数据，我们发现这个数组的ADF统计值要小于参考统计值的任何一个，并且p值还远小于任何一个参考值。
再举个例子：

# ADF Test
result = adfuller(series, autolag='AIC')
print(f'ADF Statistic: {result[0]}')
print(f'n_lags: {result[1]}')
print(f'p-value: {result[1]}')
for key, value in result[4].items():
    print('Critial Values:')
    print(f'   {key}, {value}')

结果：

ADF Statistic: 3.1451856893067296
n_lags: 1.0
p-value: 1.0
Critial Values:
   1%, -3.465620397124192
Critial Values:
   5%, -2.8770397560752436
Critial Values:
   10%, -2.5750324547306476

在这个里面ADF统计值非常的大，并且p值为100%，也就是说100%不能相信他是自回归的，这时必须进行差分。

数据差分

差分的算法就是让数据变得平稳，也就是前面给出的值变小。
我们引入一下数据集来观察一下数据在被差分后，ADF统计值的变化情况。

#未进行差分平衡
ADF Statistic: -3.5278725839643386
n_lags: 0.007299465259245383
p-value: 0.007299465259245383
Critial Values:
   1%, -3.4502615951739393
Critial Values:
   5%, -2.8703117734117742
Critial Values:
   10%, -2.5714433728242714
#已进行差分平衡
ADF Statistic: -6.704551166222008
n_lags: 3.814225674445304e-09
p-value: 3.814225674445304e-09
Critial Values:
   1%, -3.4502615951739393
Critial Values:
   5%, -2.8703117734117742
Critial Values:
   10%, -2.5714433728242714

图像变化情况：
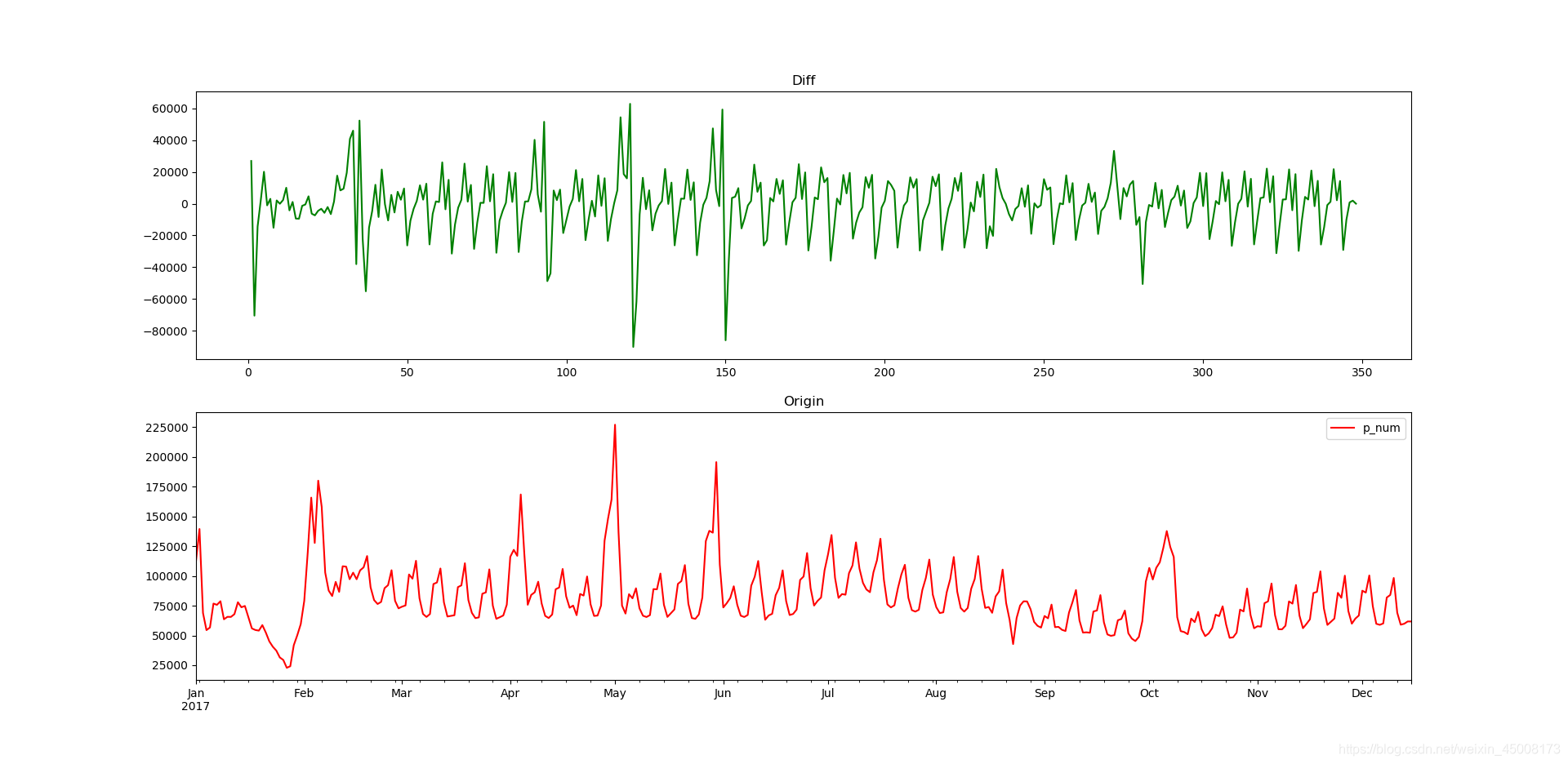
在这里插入图片描述

数据差分代码：

#参考自某GitHub博客，具体找不到是哪个兄弟写的了，如果冒犯了请见谅
def do_diff(timeSeries, maxdiff = 8):
    p_set = {}
    for i in range(0, maxdiff):
        temp = pd.DataFrame(timeSeries).copy() #每次循环前，重置
        if i == 0:
            temp['diff'] = temp[temp.columns[0]]
        else:
            temp['diff'] = temp[temp.columns[0]].diff(i)
            temp = temp.drop(temp.iloc[:i].index)  #差分后，前几行的数据会变成NaN，所以删掉

        pvalue = adfuller(temp['diff'])[1]
        p_set[i] = pvalue
        p_df = pd.DataFrame.from_dict(p_set, orient="index")
        p_df.columns = ['p_value']
        
    return temp["diff"]

ACF和PACF

两个变量的数学原理，可以参考这篇博客，写的很好
在进行ARIMA模型预测时，保证了数据的平稳之后，就是确定相关参数进行ARIMA模型建模。在AR模型中我们需要的参数时p参数，在MA模型中我们处理的是q参数，还有数据差分的次数d，这个根据需求来看。
确定p和q的方法就是通过ACF图和PACF图来进行区分。

ACF

ACF指的是自相关函数，指的是 $y_t$ 与前面 $y_{t-i}$ 之间的相关关系。公式： $\cfrac{cov(y_t,y_{t-k})}{var(y_t)}$
他的值在 $[- 1, 1]$ 之间徘徊，在平稳的数据中，随着阶数的增加该项逐渐趋向于0。

PACF

对于一个平稳AR模型，我们求出的ACF其实并不是真正的 $y_t$ 与 $y_{t-k}$ 之间严格的影响关系，这个 $y_t$ 变量还是会受到 $y_t$ 与 $y_{t-k}$ 之间数据的影响。
为了解决这个问题，我们引入了PACF这个变量，这种算法可以剔除 $y_t$ 与 $y_{t-k}$ 之间数据的影响。

代码实现

#注意，这里要引入
import statsmodels.graphics.tsaplots as sm 
def draw_acf_and_pacf(serise,lag=20):
	# 绘图
	f = plt.figure()
	ax1 = f.add_subplot(211)
	sm.plot_acf(serise, lags=20, ax=ax1)

	ax2 = f.add_subplot(212)
	sm.plot_pacf(serise, lags=20, ax=ax2)
	plt.show()

出图结果：
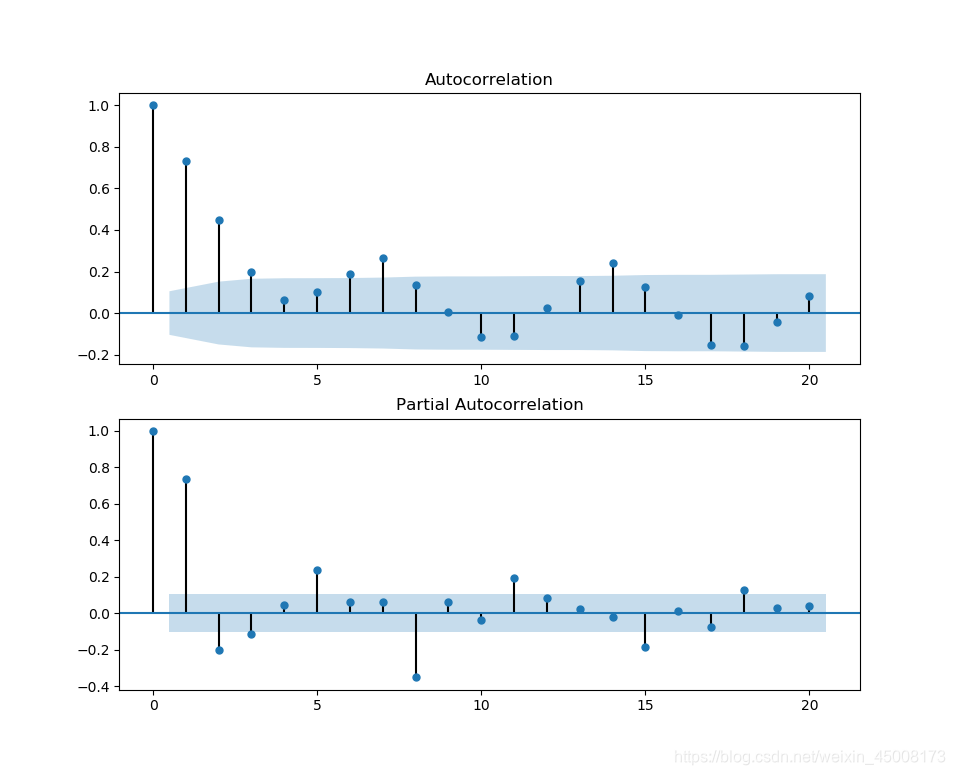
在这里插入图片描述

上图表示的是在不同阶数下，ACF和PACF系数的变化情况。

图1为ACF，图2是PACF，这个图的横坐标表示的是k的值，也就是 $y_t$ 与 $y_{t-k}$ 的那个k。
阴影区域表示的是置信区间，由于这时我们要对q和p这两个参数进行估计，我们选择p/q时，系数是否落到置信区间作判断。

选择p和q的原则：
看第三行
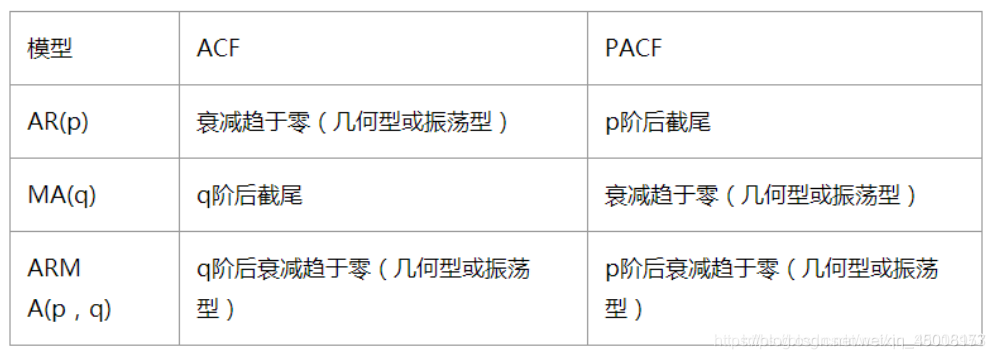
在这里插入图片描述

由上图分析我们选择

p 可以选 4，6差不多合适
q 可以选 4，5差不多合适
d = 0 由于没有作差分，故为0

接下来为了判断我们选的p和q是否正确，可以通过一些标准来进行判断。

但是这个标准是否符合我们的需求，我们需要通过AIC进行检验来判断，这里给出AIC检验的热力图：
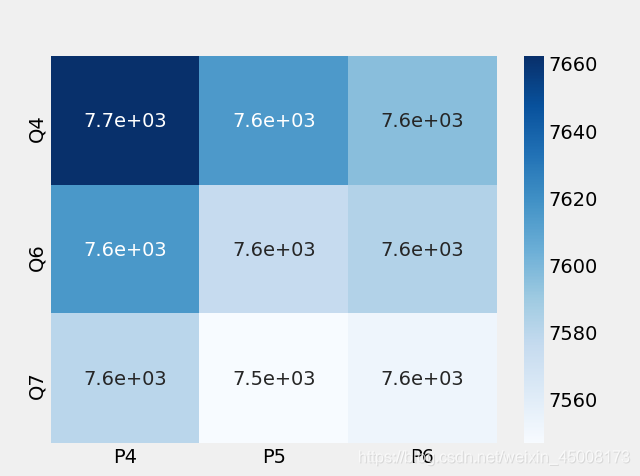
在这里插入图片描述
通过上图比较可以发现，P5，Q7是比较符合我们的需求的，同时我们也可以给出诊断图：

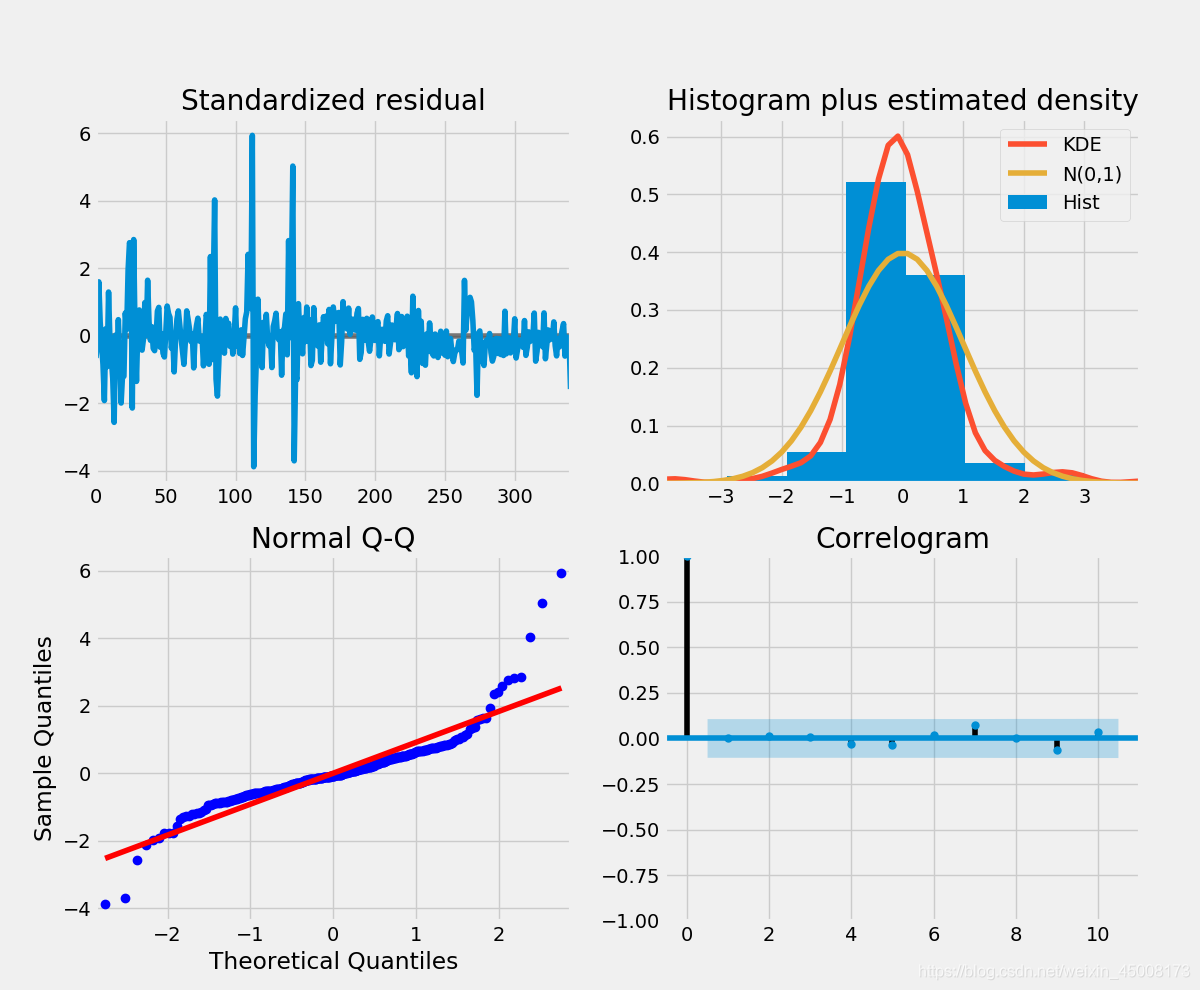
在QQ图中发现点除了一些点不在该条线上，其他的效果还好。
将参数导入模型中，进行拟合，我们可以获得结果:
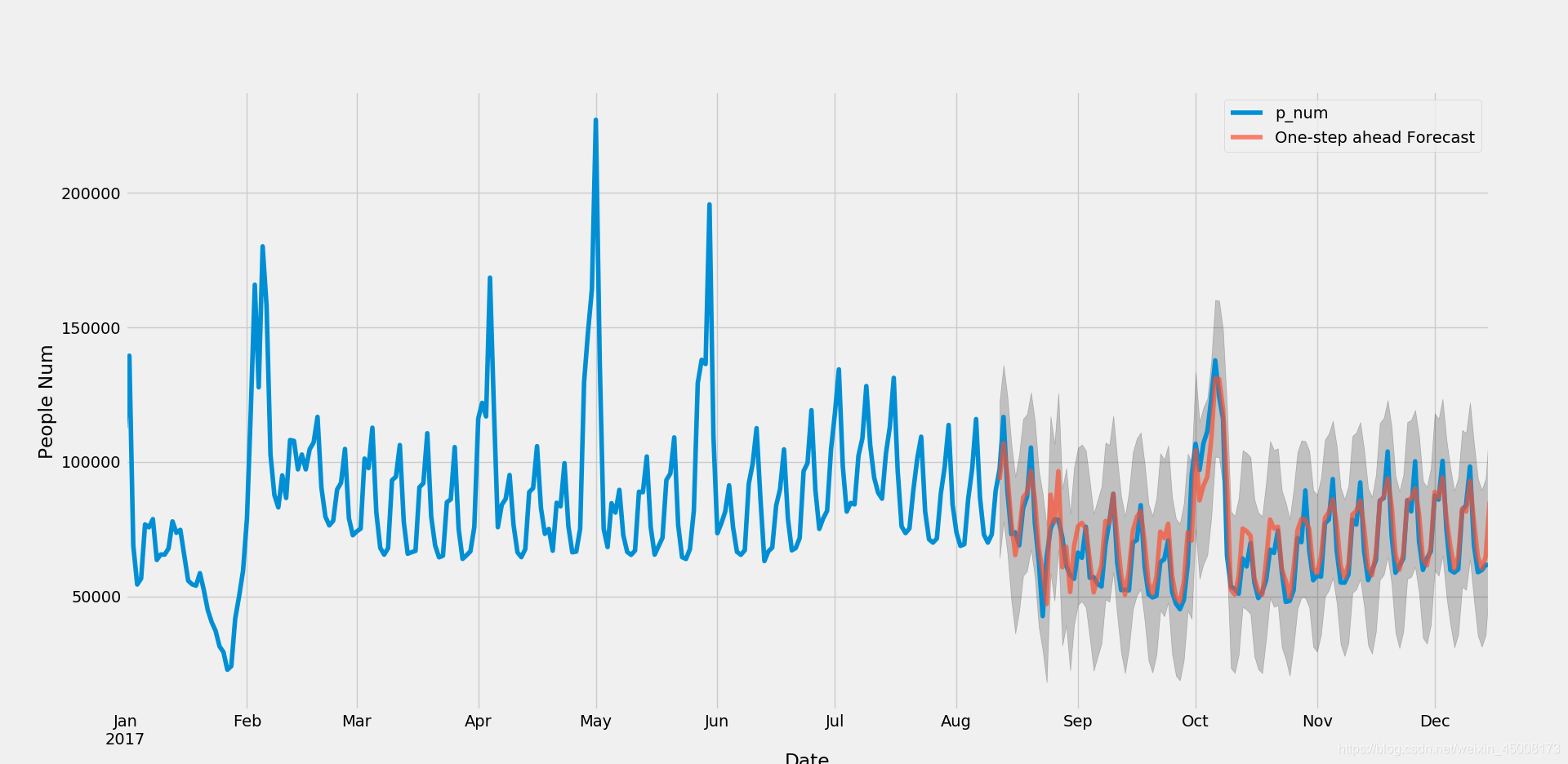
在这里插入图片描述

全代码解释：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
import statsmodels as sm 
from statsmodels.tsa.arima.model import ARIMA
import itertools
import seaborn as sns
plt.style.use('fivethirtyeight')
def do_diff(timeSeries, maxdiff = 8):
    p_set = {}
    for i in range(0, maxdiff):
        temp = pd.DataFrame(timeSeries).copy() #每次循环前，重置
        if i == 0:
            temp['diff'] = temp[temp.columns[0]]
        else:
            temp['diff'] = temp[temp.columns[0]].diff(i)
            temp = temp.drop(temp.iloc[:i].index)  #差分后，前几行的数据会变成nan，所以删掉

        pvalue = adfuller(temp['diff'])[1]
        p_set[i] = pvalue
        p_df = pd.DataFrame.from_dict(p_set, orient="index")
        p_df.columns = ['p_value']
        
    return temp["diff"]

def draw_acf_pacf(serise,lag=20):
	# 绘图
	f = plt.figure(facecolor='white')
	ax1 = f.add_subplot(211)
	sm.plot_acf(serise, lags=20, ax=ax1)

	ax2 = f.add_subplot(212)
	sm.plot_pacf(serise, lags=20, ax=ax2)
	plt.show()
	return serise
# df = pd.read_csv('./TimeSeries/all.csv',encoding='gb2312')#gb2312是中文编码,utf-8不能解决中文编码的问题
     
# df_new = pd.DataFrame({"p_num":list(df['人数'])},index=list(df['时间']))
# df_new.plot()
# plt.show()
#读取数据
xls = './TimeSeries/all_1.xlsx'
df = pd.read_excel(xls,sheet_name=0)
df = df[(df['出发地']=='广州')&(df['目的地']=='深圳')]
df_mod = pd.DataFrame({"p_num":list(df["人数"])},index=list(df["时间"]))

#平稳性检验
serise = df_mod.loc[:,"p_num"].values
result = adfuller(serise, autolag='AIC')
# print(f'ADF Statistic: {result[0]}')
# print(f'n_lags: {result[1]}')
# print(f'p-value: {result[1]}')
# for key, value in result[4].items():
#     print('Critial Values:')
#     print(f'   {key}, {value}')  

#分析发现，ADF统计值小于任何一个得到的统计值，并且p值也小于任何一个置信区间的值，我们可以确定曲线是平稳的

#如果不平稳则要进行差分计算,函数best_diff
diff_s = do_diff(serise)
diff_s_2 = do_diff(diff_s)
result = adfuller(serise, autolag='AIC')
# print(f'ADF Statistic: {result[0]}')
# print(f'n_lags: {result[1]}')
# print(f'p-value: {result[1]}')
# for key, value in result[4].items():
#     print('Critial Values:')
#     print(f'   {key}, {value}')
    
# fig,axes = plt.subplots(nrows=2,ncols=1)
# diff_s.plot(style='g-',ax=axes[0],title ='Diff')
# df_mod.plot(style='r-',ax=axes[1],title ='Origin') 
# draw_acf_pacf(serise)
p = [4,5,6]
q = [4,6,7]
d = [0,0,0]
pdq = list(itertools.product(p, d, q))

# seasonal_pdq = [(x[0], x[1], x[2], 12)#季节性的
#                 for x in list(itertools.product(p, d, q))]
# print(seasonal_pdq)
import warnings
warnings.filterwarnings("ignore") # specify to ignore warning messages
dataF = pd.DataFrame({"P4":[0,0,0],"P5":[0,0,0],"P6":[0,0,0]},index=["Q4","Q6","Q7"])
for param in pdq:
    model = ARIMA(df_mod,order=param,enforce_stationarity=False,enforce_invertibility=False)
    results = model.fit()
    AIC = results.bic
    dataF.loc["Q"+str(param[2]),"P"+str(param[0])] = int(AIC)
    print('ARIMA{} - AIC:{}'.format(param,AIC))

sns.heatmap(dataF,annot=True,cmap="Blues",cbar=True)
model = ARIMA(df_mod,order=(6,0,7),enforce_stationarity=False,enforce_invertibility=False)
results = model.fit()
#results.plot_diagnostics(figsize=(12, 12))
#获取预测结果
pred = results.get_prediction(start=pd.to_datetime('2017-08-12'), dynamic=False)
pred_ci = pred.conf_int()
#画图
ax = df_mod['2017/1/1':].plot(label='Observed',figsize=(12, 6))
pred.predicted_mean.plot(ax=ax, label='One-step ahead Forecast', alpha=.7)
#置信区间
ax.fill_between(pred_ci.index,
                pred_ci.iloc[:, 0],
                pred_ci.iloc[:, 1], color='k', alpha=.2)
 
ax.set_xlabel('Date')
ax.set_ylabel('People Num')
plt.legend()
 
plt.show()