Python基于季节性自回归移动平均模型(SARIMA模型)进行时间序列分析建模项目实战

说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景

SARIMA是季节性自回归移动平均模型。对于周期性时间序列，首先需要去除周期性，去除的方式是在周期间隔上做一次ARIMA，此时可以得到一个非平稳非周期性的时间序列，然后在此基础之上再一次使用ARIMA进行分析。

本项目应用SARIMA算法进行建模、预测、分析，形成一个完整的项目实战内容。

2.数据获取

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

 

数据详情如下(部分展示)：

3.数据预处理

3.1 用Pandas工具查看数据

使用Pandas工具的head()方法查看前五行数据：

 关键代码：

3.2数据缺失查看

使用Pandas工具的info()方法查看数据信息：

从上图可以看到，总共有2个变量，数据中无缺失值，共65条数据。

关键代码：

 

3.3数据描述性统计

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

 关键代码如下：

4.探索性数据分析

4.1 x1变量时间序列分析图

5.构建SARIMA时序模型

5.1 SARIMA模型关键点介绍

SARIMA结构参数有七个：(p,d,q) (P,D,Q,s)

p：代表预测模型中采用的时序数据本身的滞后数(lags) ,也叫做AR/Auto-Regressive项。

d：代表时序数据需要进行几阶差分化，才是稳定的，也叫Integrated项。

q：代表预测模型中采用的预测误差的滞后数(lags)，也叫做MA/Moving Average项。

P: 周期性自回归阶数。

D: 周期性差分阶数。

Q: 周期性移动平均阶数。

s: 周期时间间隔。

5.2序列平稳性检验

图5.2-1 原始序列的时序图

此图显示该序列2017年波动很大，2021年到2022年波动相对平稳，可以判断为弱平稳序列。

图5.2-2 原始序列的自相关图

此图的自相关图显示自相关系数整体在-0.2到0.2之间徘徊，说明序列间具有弱短期相关性。

表5.2-1　原始序列的单位根检验

此表单位根检验统计量对应的p值小于0.05，说明该序列为平稳序列。

5.3对原始序列进行一阶差分，并进行平稳性和白噪声检验

1）对一阶差分后的序列再次做平稳性判断。

 图5.3-1　一阶差分之后序列的时序图

图5.3-2　一阶差分之后序列的自相关图

表5.3-1 一阶差分之后序列的单位根检验

结果显示，一阶差分之后序列的时序图在均值附近比较平稳地波动、自相关图有很强的短期相关性、单位根检验p值小于0.05，所以一阶差分之后的序列是平稳序列。

2）对一阶差分后的序列做白噪声检验

表5.3-2　一阶差分之后序列的白噪声检验

此表输出的p值远小于0.05，所以一阶差分之后的序列是平稳非白噪声序列。

5.4对一阶差分后的序列拟合SARIMA模型

下面进行模型定阶。模型定阶就是确定p、d、q、P、D、Q、s。

第一种方法：人为识别，根据下图进行模型定阶。 

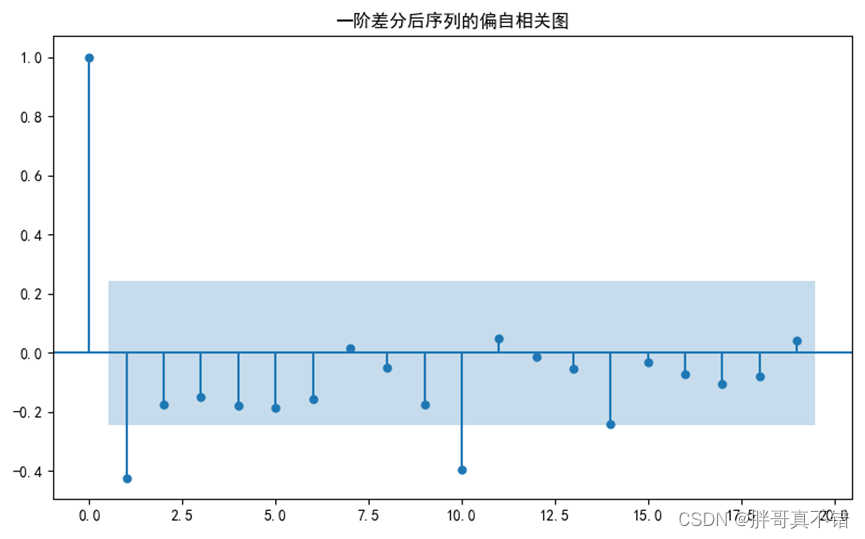
图5.4-1　一阶差分后序列的偏自相关图

一阶差分后自相关图显示出1阶截尾，偏自相关图显示出拖尾性，所以可以考虑用MA(1)模型拟合1阶差分后的序列，即对原始序列建立SARIMA(order=(0，1，1))模型。

第二种方法：相对最优模型识别(建议大家使用这种方式)。

计算SARIMA(order=(p，d，q), seasonal_order=(P,D,Q,s))，采用多种组合的方式，获取所有组合的BIC信息量，取其中BIC信息量达到最小的模型阶数。

计算完成BIC矩阵如下：

当p值为0、q值为0、P值为0、Q值为1、s值为12时，最小BIC值为143.5571。此时模型定阶完成。

用AR(0)模型拟合一阶差分后的序列，即对原始序列建立SARIMA(order=(0，0，0), seasonal_order=(0,1,1,12))模型。下面对一阶差分后的序列拟合SARIMA模型进行分析: 

1.参数检验和参数估计见下表:

表5.4-1 模型参数

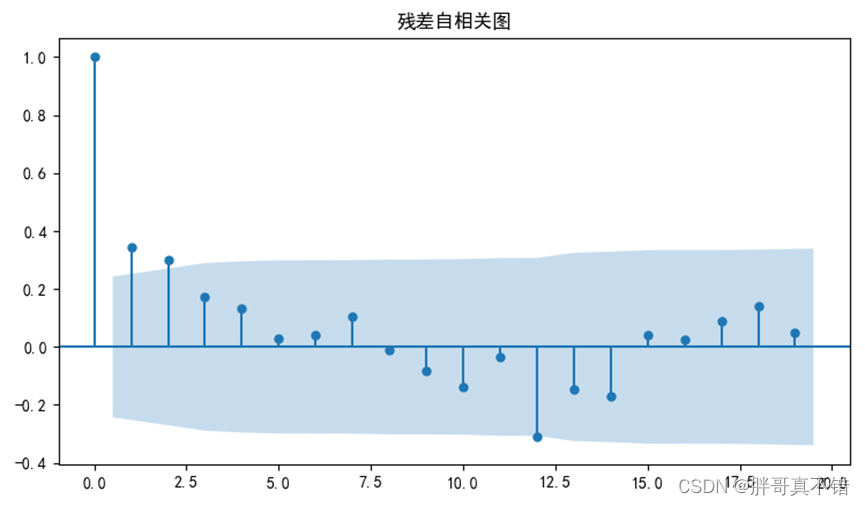
2.模型检验之残差检验：

 图5.4-2　残差自相关图

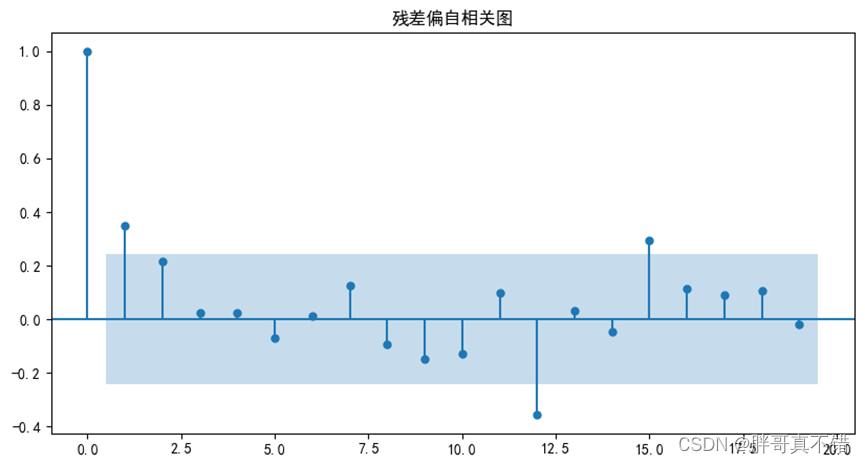
图5.4-3　残差偏自相关图 

图5.4-4　残差偏自相关图

D-W检验：

DW值显著的接近于0或４时，则存在自相关性，而接近于２时，则不存在（一阶）自相关性。

D-W检验的结果为：1.3132。因此，模型预测的残差不存在自相关性性，这说明拟合的模型预测效果很好。

残差序列的白噪声检验结果为：([8.01950276]), ([0.00462763])，可以看出p值为0.00462， P<0.05。

5.5 SARIMA模型预测

应用SARIMA(order=(0，0，0), seasonal_order=(0,1,1,12))对项目数据做为期5个月的预测，结果如下表所示：

表5.5-1 预测未来5个月的数据

6.结论与展望

综上所述，本文采用了季节性自回归移动平均模型算法来构建时间序列分析模型，通过计算BIC信息量找到最优的参数值，最终证明了我们提出的模型效果很好。

# 本次机器学习项目实战所需的资料，项目资源如下：
 
# 项目说明：

# 链接：https://pan.baidu.com/s/14CNWQ7QZscLvS-yrRJBLkg 
# 提取码：pwx9

print('****************查看数据前5行********************')
print(data.head())
print('****************数据缺失查看********************')
print(data.info())
print('****************数据描述性统计分析********************')
print(data.describe())

data = data.set_index('月份')

# 时序图

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
data.plot(color='green', marker='o', linestyle='dashed', linewidth=1, markersize=6)
plt.ylabel('x1')
plt.title("x1时间序列分析图")
plt.show()