关于EM算法（Expectation Maximization）

EM算法是一个解决类似先有鸡还是先有蛋的问题

EM算法想解决的问题：手里有一堆sample data，但是data的部分信息缺失，称这部分丢失的信息为隐变量（隐变量是真实存在的客观信息，只是因丢失而不被知道），同时产生这些data的distribution含有未知参数。即data信息有缺失，originating distribution信息也有缺失的情况下如何同时得到两者的信息。

X表示data，Z表示隐变量, θ表示概率分布的参数

motivation：1.已知distribution时，即知道(X, Z)的联合概率，可以容易地计算隐变量的后验概率P(Z|X)，只需要使用贝叶斯公式即可                 

                     2.已知数据的全部信息时，只需要使用极大似然估计，即可获得分布参数的最佳估计

因此将两者结合起来，迭代进行求解。

标准的EM算法：

1.初始化参数θold

2.E步：E表示E(log likelyhood)，E[ log P((X, Z)|  θ)]是对完整数据的似然函数求期望,下式即似然函数的期望

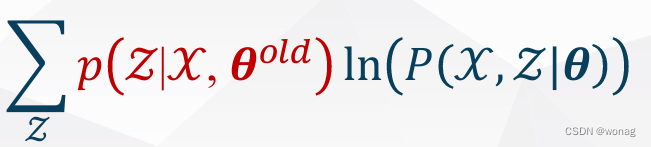   #z连续情况改求和为积分即可

#Z的后验概率使用贝叶斯定理计算，该式整体是对完整数据似然函数的一种加权，利用θold得到的z分布对data进行加权，得到期望的完整数据

                助力理解的小例子：z后验取1/-1概率均为1/2   手头的data为(1,2)   则可以认为完整数据为0.5个((1,2),  1)和0.5个((1, 2),  -1)，此时的似然函数也就分裂成了两个，需要对他们求期望

3.M步： 对上面求得的函数求极值即可，E步得到θ的单参量函数，即期望似然函数，记为Q

4.返回2步循环

GMM:高斯混合模型

使用了一种启发式的EM算法，不是标准的EM算法，因为其极大化的是不完整数据的似然函数

一维情况：

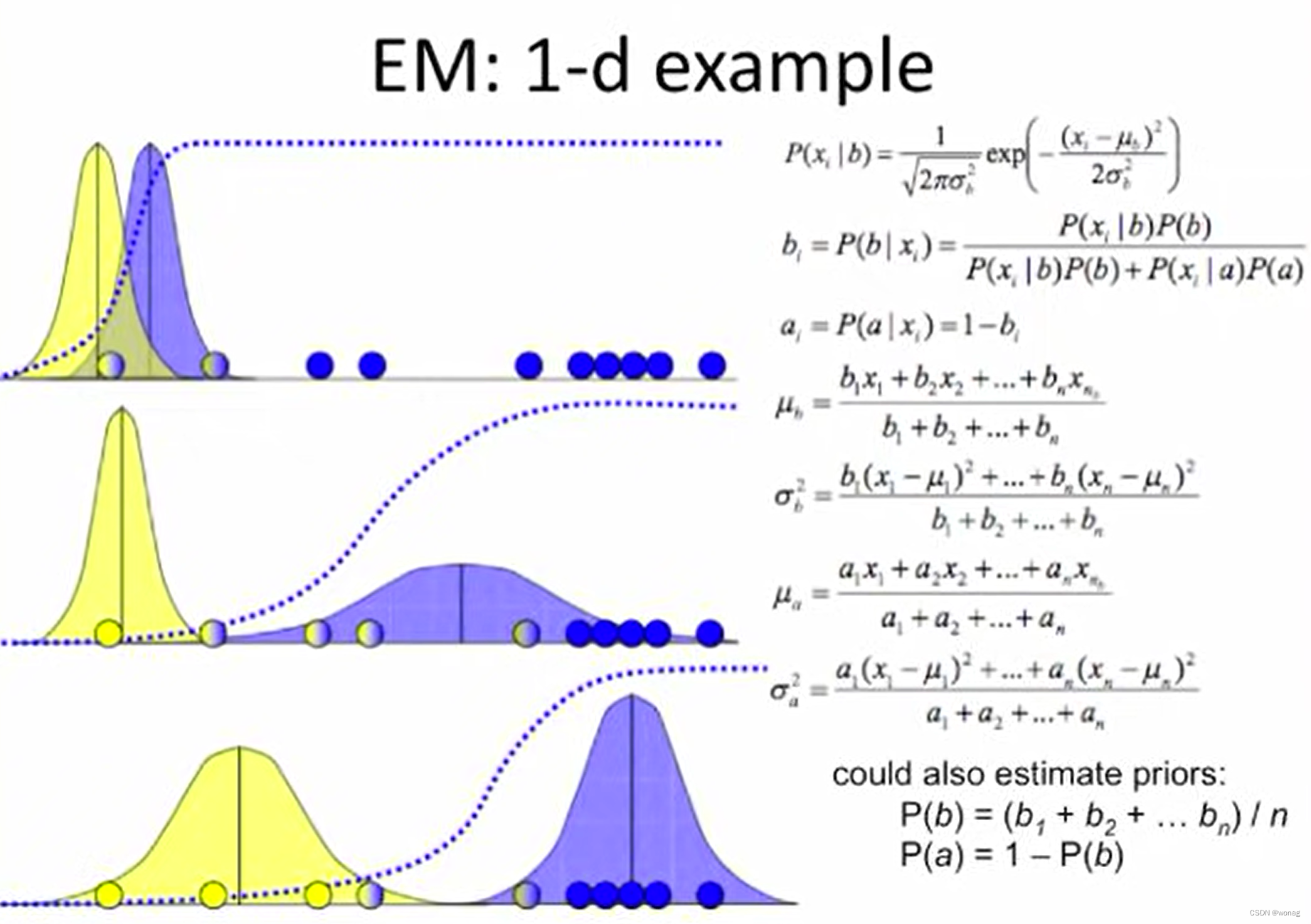
高维情况：

另一种常见写法：ri,k即xi样本属于class k的后验概率

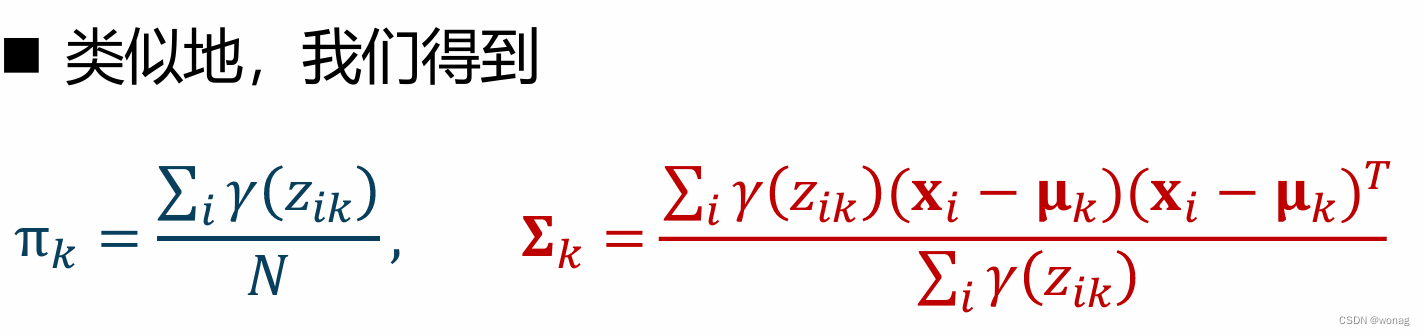
本质上其实没有得到什么迭代关系，而是函数取极值时的三个耦合在一起的三参量方程，我们硬把三个参量单独挪到等式一边，以期望得到迭代关系，这和迭代求解线性方程组十分相似。

后续：GMM算法使用的是标准的EM算法，只是推导较为冗长，结果竟然和上述迭代方程一致

注：详细推导见B站白板推导up