矩阵的特征值估计

特征值实虚部估计：

矩阵越不对称，特征值的虚部越大，反Hermite矩阵的特征值为纯虚数。

矩阵的行列式/特征值之积估计：

行列式不大于各列模长之积

严格对角占优矩阵的行列式估计

矩阵的特征值平方和估计：

特征值平方和不大于Frobenius范数的平方

正规矩阵上式取等

特征区域估计：

特征区域估计：矩阵的盖尔圆以最大连通分量为单元，连通分量里有几个盖尔圆，就有几个特征值

更强的盖尔圆定理：矩阵的特征值λ在矩阵的第i行盖尔圆中，i为特征向量x中最大模元素index

特征值的隔离：利用相似矩阵具有相同特征值，求相似矩阵的盖尔圆，利用对角阵作P等效于调节盖尔圆半径，使不同盖尔圆不相交

找到一个控制矩阵B，可以利用B调整盖尔圆半径

利用行半径和列半径共同调节盖尔圆半径，取定二者比例α，就得到一组盖尔圆

用一组卡西尼卵形线作区域

可约矩阵与不可约矩阵

可约矩阵：存在P置换阵，使得下式成立，其中C11,C22为方阵，则称方阵A是可约的

不可约矩阵:找不到P

矩阵的可约与不可约的图判别方法：以n个顶点代表n个对角元。若 一个非对角元素非零，则作一条从与它 同行对角元的那个顶点到与它同列对角 元的顶点的有向线段。不可约矩阵的任意两节点之间都存在有向路径连通，可约矩阵存在节点p，q，无法从p到达q。

矩阵按行/列严格对角占优，则矩阵可逆

谱半径的估计：

对谱半径不大于矩阵1范数和无穷范数的推广，α=0即1范（1范数：max列和；∞范数：max行和）

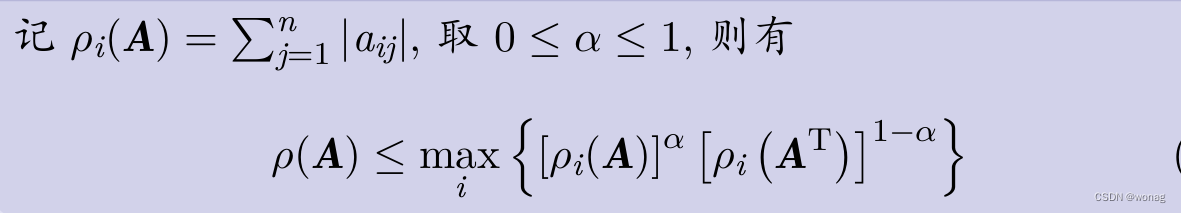
α取1/2，利用i行之和，i列之和计算

注：

广义特征值问题：

该问题存在n个特征值及n个完备的（线性无关的）特征向量

一组向量满足如下条件称为按B标准正交（B为任何矩阵）

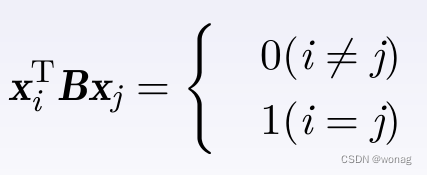
无论B为何矩阵，都有：所有向量非0，且为线性无关向量组

Rayleigh商：

实对称矩阵的Rayleigh商

R(kx) = R(x) 

max R(x) = max λ   min R(x) = min λ    (针对实对称阵成立，所有向量都可以向标准正交特征向量组投影，向量x的R(x)为各个特征向量分量对应的特征值的加权平均，以投影系数的平方为权重)

R(x)的驻点是矩阵的特征向量

利用Rayleigh商求特征值的极大极小原理：

(针对广义特征值问题，更改R(x)为即可，结论不变)