矩阵常识与jordan标准型

1.换基过渡矩阵，坐标变换公式

        [y1, y2, y3] = [x1, x2, x3]C  #y为新基，x为旧基，注意y1对应于C中的一列

        新坐标= 旧坐标

2.线性变换的矩阵表示，在不同基下的矩阵表示

        

        

关于矩阵A的最小零化多项式：

最小多项式（最高次系数为1）可以整除任何零化多项式（最高次系数为1）

最小多项式的零点分布和特征多项式的零点分布相同（不考虑零点重数）

最小多项式求法：=最大不变因子

selvester定理：AB和BA的特征值只差在0特征值的个数上，非0特征值的数量和分布完全一致

jordan标准型：

特征多项式的零点分布重数情况直接决定了jordan标准型中块的可能大小，其实就是把特征多项式拆拆合合

矩阵A的jordan标准型在不考虑块之间的顺序的情况下是唯一的

 Jordan标准型是一整个“相似矩阵大家族”的典型代表，即表示同一个线性变换大家族的典型代表

计算方法：计算矩阵的各阶行列式因子（k阶子式的最大公因式）Dk，计算不变因子,将所有不变因子拆分为初等因子组，每个初等因子对应一个jordan块

jordan块的幂次计算：将幂次看作函数作用于jordan块上

正规矩阵

任何方阵都可以正交相似于上三角矩阵，但是只有正规矩阵可以正交相似于对角阵

1.对称变换是定义在内积上的

2.正交变换也可以定义在内积上，本质是线性变换前后范数不变

3. 2个子空间的和是直和即2个子空间没有交集（除了0元素），两个子空间之间线性无关

关于内积

        欧几里得空间：实内积实线性空间

        酉空间：复内积复线性空间（复内积满足正定性，<x, x> >=0 自己和自己的内积均为实数）

        cauchy-schwarz不等式是使用内积书写的，作为内积的一条性质，以内积形式记忆

<x,  y> <y,  x> <=  <x,  x>  <y,  y>(复)            <x,  y>^2  <=  <x,  x>  <y,  y>(实)

       度量矩阵：基内积矩阵，恒对称正定(由于内积的正定性)，在此基下，计算任意两个向量x,  y的内积为x^TAy(x,  y为基下坐标)

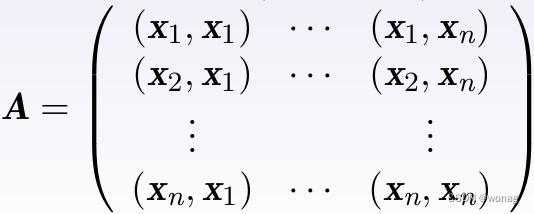
        任意对称正定矩阵都可以作为一组基的度量矩阵，于是定义一个内积等价于，定义一个对称正定矩阵(再任选一组基)

        一个内积在不同基下的度量矩阵合同，C取过渡矩阵（应用：与正定矩阵合同的矩阵正定）

        线性无关是向量自身的性质，和基无关，线性无关的向量在任意一组基下的坐标均线性无关

        线性变换的特征向量和特征值是线性变换自身的性质，不依赖于基的选择

求解微分方程：

上图中的积分号为不带+C的结果，即只有最后c一个自由量