概率幅和概率(Probability Amplitude and Probability)

概率幅

在量子力学里，概率幅，又称为量子幅（英语：Probability amplitude），是一个描述量子行为的复数量。事实上是表示初始量子态（ψi）和终末量子态(ψf)的两个希尔伯特矢量的内积（<ψf, ψi>）；而这个概率幅的绝对值平方就是与从状态ψi跃迁到状态ψf的概率密度P：

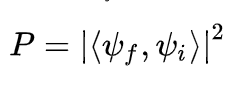
非相对论量子力学

在不可考虑狭义相对论的状况下，物理上假设微观粒子的纯态都可以用波函数代表，而在这种情况下，若ψ:R^3→C和ϕ:R^3→C各为两个表纯态的平方可积波函数，那这样两者间的概率幅就是：

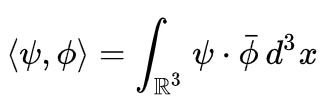
概率幅（Probability amplitude）和概率（Probability）

概率幅（Probability amplitude）和概率（Probability）是量子力学中密切相关的两个概念，但它们有着不同的物理意义和数学定义。

1. 概率幅（Probability Amplitude）

在量子力学中，系统的状态由一个波函数（wave function）或态矢量来描述，通常表示为 ψ（或 ∣ψ〉 ）。这个波函数的每个位置 x 或动量 p 对应的复数值称为概率幅，记为ψ(x)或〈x∣ψ〉。

• 性质：

• 概率幅是一个复数，通常写成 ψ(x)=a+bi（其中 a 和 b 是实数，i 是虚数单位）。

• 概率幅的大小与一个事件发生的可能性相关，但本身并不能直接表示概率。

• 在数学上，概率幅的平方的模值（绝对值的平方）给出概率。

• 数学表达： 如果粒子处于状态 ∣ψ〉，那么该粒子在位置 x 处被发现的概率幅是： ψ(x)=〈x∣ψ〉

其中，〈x∣ψ〉 是量子态 ∣ψ〉 在位置态 ∣x〉 下的投影。

2. 概率（Probability）

概率是一个实数，表示某个事件发生的可能性，数值范围为 0 到 1。在量子力学中，粒子在某个位置被发现的概率与概率幅的绝对值平方相关联。

• 数学定义： 如果某个量子态的概率幅为 ψ(x)，那么粒子在位置 x 被找到的概率 P(x) 是： P(x)=∣ψ(x)∣^2 其中，∣ψ(x)∣^2 是概率幅的复数模平方，即： ∣ψ(x)∣^2=ψ(x)ψ∗(x)

这里 ψ∗(x) 是概率幅的共轭复数。

概率幅与概率的关系

• 概率幅是一个复数，包含了事件发生的幅度和相位信息。

• 概率是概率幅的模平方，即 ∣ψ(x)∣^2，是一个实数，表示某事件发生的可能性。

举例

假设一个粒子的波函数 ψ(x)=0.6+0.8i，则：

• 概率幅 ψ(x)=0.6+0.8i，这是一个复数。

• 概率 P(x)=∣ψ(x)∣2=(0.6)^2 + (0.8)^2 =1，表示该粒子在该位置的概率为 1（即该位置确定有粒子）。

参考资料：

https://zh.wikipedia.org/wiki/%E6%A9%9F%E7%8E%87%E5%B9%85