关于梯度提升树残差（李航机器学习）的一些理解（附代码）

LegendNeverDied-24

已于 2024-11-23 20:44:48 修改

阅读量1.1k

点赞数 3

分类专栏：机器学习文章标签：算法机器学习

于 2020-01-27 23:34:02 首次发布

本文链接：https://blog.csdn.net/weixin_45424997/article/details/104095424

版权

机器学习专栏收录该内容

3 篇文章

订阅专栏

本文基于李航的《统计学习方法》探讨了梯度提升树中残差与负梯度的关系。在平方误差损失函数下，残差等同于负梯度。对于一般损失函数，每个决策树学习的是负梯度。文章对比了GBDT和XGBoost的优化方法，指出XGBoost利用二阶导数信息进行牛顿法优化。同时，提供了书上例题的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

恰逢最近在学习提升树（boosting tree）算法，参考了李航统计学习方法（第二版），但仍觉有一些疑惑，遂上网看了很多资料但仍感觉有些细节不清楚，主要原因是网上的公式符号使用自成一体，且一些结论缺少具体推理，于是以李航统计学习书上的公式表达为基础，记录一些思考。
一：采用平方误差损失函数时损失函数的负梯度就是提升树的残差
首先在书8.4节，167页，当损失函数为负梯度时：
在这里插入图片描述
其中

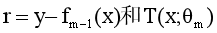
分别代表真实值与第m-1个模型预测值的残差，以及第m课我们想要学习的树。
从损失函数（1）中可以看出，第m棵树学习的是如何逼近残差r。当学习了第m个树T以后，由加法模型第m个模型为：

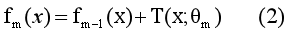
因为这里损失函数为平方误差损失函数，所以对于学到的第(m-1)个模型f_m-1(x) 有
在这里插入图片描述
可以看出（3）对f_m-1(x) 导数的负值（负梯度）就是残差r，所以为什么采用平方误差损失函数时损失函数的负梯度就是提升树的残差。

网上还有人用二阶泰勒展开来解释上面的结论。
在这里插入图片描述
这里提供一个详细推到版：由式（2）(4),将第m个模型的损失函数写为

将g和h带入得（6）

我们希望学习一个树T(x; $\theta~m~$ )来使得损失函数（6）最小化，很明显（6）是关于T(x; $\theta~m~$ )的二元二次凹函数（f_m-1(x)为上一步学习的模型），其极小点在“-b/2a”处取得（牛顿法）所以
在这里插入图片描述
每一次树学习的（叶子节点的值）都是第上一个模型结果与真实标签的残差。
二：当采用一般损失函数时，第m棵树学习的是损失函数对第m-1个模型的负梯度
梯度下降算法：对于损失函数L( $\theta$ ),我们希望通过迭代 $\theta$ 来最小化损失函数以求得最优的 $\theta$ 即：
在这里插入图片描述
而对于梯度提升算法的损失函数L(y,f_m(x)),同样我们也可以通过迭代f(x)获得一个使损失函数最小的模型f_m(x).

比较(2)和(8)可得

所以对于一般损失函数，每个决策树拟合的都是负梯度。

三：GBDT与XGboost的区别
GBDT的原理实际上是函数空间的梯度下降法：
在这里插入图片描述
XGboost的原理实际上是函数空间的牛顿法：

因为牛顿法的推导是基于损失函数二阶泰勒展开，而梯度下降法只需要一阶导数的信息.“牛顿法是用一个二次曲面拟合你当前所处位置的局部曲面，梯度下降法是用一个平面去拟合当前局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径”.

GBDT每次迭代，都会根据模型f_m-1(x)，计算出损失函数的负梯度，去更新叶节点，然后更新f_m(x)得到当前模型
XGboost每次迭代，都会根据模型f_m-1(x)，算出损失函数对其的一阶导和二阶导，去更新叶节点，然后更新f_m(x)得到当前模型。
GBDT和XGboost在更新叶结点时，都是通过牛顿法得到使L(y,f_m-1(x)+T(x, $\theta$ _m))最小的T的叶子节点的值

XGboost的高度概括：“把样本从根分配到叶子结点，本质是一个排列组合，而不同的组合对应不同的损失函数，我们要优化寻找的，就是使得损失函数达到最小值的那一种组合方案”

代码（书上例题）：

# coding=utf-8
import numpy as np

label = np.array([5.56, 5.7, 5.91, 6.4, 6.8, 7.05, 8.9, 8.7, 9, 9.05])
feature = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

class Tree_model(object):
    def __init__(self, split, mse, left_value, right_value, residual):
        '''
        split: 为feature最佳切割点
        mse: 为每棵树的平方误差
        left_value: 为决策树左值
        right_value: 为决策树右值
        residual: 为每棵决策树生成后余下的残差
        '''
        self.split = split
        self.mse = mse
        self.left_value = left_value
        self.right_value = right_value
        self.residual = residual

"""
第一步：
设置特征的切分点
输入:特征feature
输出：切分点splitpoint
"""
def Split_point(feature):
    f1=list(feature.copy())
    f2=list(feature.copy())
    splitpoint=(np.array(f1)[0:-1]+np.array(f2)[1:])/2
    return splitpoint

"""
第二步：
建立CART回归树
输入：分裂点：split_point,特征值：feature（list）,残差：label(矩阵)
输出：子树：Tree，残差：Residual
"""
def Build_desicion_tree(split_point,feature,label):
    m_s=[]
    c1=[]
    c2=[]
    #建立三个表：m(s),c1,c2，对每一个分裂点计算m(s)，c1,c2
    for i in range(split_point.shape[0]):
        label_left=label[0:int(split_point[i])]#位于分裂点左边的label
        label_right = label[int(split_point[i]):]#位于分裂点右边的label
        c1.append(np.mean(label_left))
        c2.append(np.mean(label_right))
        m_s.append(np.sum((label_left-c1[i])**2)+np.sum((label_right-c2[i])**2))
    spilt_posi=np.argmin(m_s)#返回m_s最小值所在的位置
    best_split=split_point[spilt_posi]#最佳分裂位置
    best_mse=m_s[int(spilt_posi)]#最佳均方误差
    left_value=np.mean(label[0:int(best_split)])#左树的label值
    right_value=np.mean(label[int(best_split):])#右树的label值
    residual=np.concatenate((label[0:int(best_split)]-left_value,label[int(best_split):]-right_value,))
    Tree=Tree_model(best_split, best_mse, left_value, right_value, residual)
    return Tree,residual

"""
第三步：
建立提升树
输入:特征feature，标签label，树的个数tree_unm
输出：回归的提升树Trees
"""
def Build_boosting_tree(feature,label,tree_num=6):
    split_point=Split_point(feature)
    Trees=[]
    residual=label.copy()
    for num in range(tree_num):
        Tree,residual=Build_desicion_tree(split_point,feature,residual)
        Trees.append(Tree)
    return Trees


"""
第四步：
对feature的每个值进行预测
输入：Trees，feature
输出：prediction
"""
def Predict_Tree(Trees,feature):
    prediction=np.zeros((feature.__len__()))
    for Tree in Trees:
        for i in range(feature.__len__()):
            if feature[i]<Tree.split:
                prediction[i]=prediction[i]+Tree.left_value
            else:
                prediction[i]=prediction[i]+Tree.right_value
    return prediction

if __name__ == '__main__':
    Trees=Build_boosting_tree(feature,label)
    prediction=Predict_Tree(Trees,feature)
    print(prediction)