一致代价搜索问题（含样例推导+伪代码）

最新推荐文章于 2022-03-03 13:26:28 发布

gtl0110

最新推荐文章于 2022-03-03 13:26:28 发布

阅读量3.4k

点赞数 2

本文链接：https://blog.csdn.net/weixin_45472668/article/details/120679792

版权

一致代价搜索图搜索最短路径算法实现路径优化

关键词由CSDN通过智能技术生成

一致代价搜索问题

问题描述

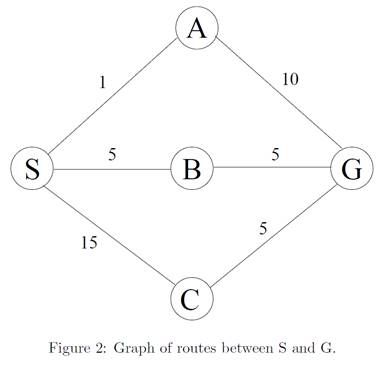
 Consider the graph shown in Figure 2. Let S be the initial state and G be the goal state.
The cost of each action is as indicated. （搜索求解☆☆☆☆）
(a) Give a trace of uniform-cost search.
(b) When A generates G which is the goal with a path cost of 11, why doesn’t the algorithm halt and return the search result since the goal has been found? With your observation, discuss how uniform-cost search ensures that the shortest path solution is selected.

问题分析

本次讨论的主题是一致代价搜索（UCS uniform-cost search）

基本原理

一致代价搜索是在广度优先搜索上进行扩展的，也被成为代价一致搜索，他的基本原理是：一致代价搜索总是扩展路径消耗最小的节点N。N点的路径消耗等于前一节点N-1的路径消耗加上N-1到N节点的路径消耗。

算法实现

数据结构：探索集(closed表表示已扩展的结点集合)、边缘（开节点表 open表表示待扩展的结点）、parent表

算法步骤：

如果边缘为空，则返回失败。
否则从边缘中选择一个叶子节点。
目标测试：通过返回，否则将叶子节点的状态放入中。
遍历叶子节点操作：
1. 产生子节点，如果不在open也不在close中，则插入open
2. 如果close中存在且有更高的路径消耗，则用子节点代替close中的状态

样例推导

初始化 $closed={\empty},open=\{S\}$
$o p e n . i s e m p t y () = = f a l s e$ ，从 $o p e n$ 中选择S。

S不是目标节点，生成子节点A(1)，B(5)，C(15)三者都不在open和closed中，因此插入open，并进行排序。 $open=\{A,B,C\},closed=\{S\}$

A S B G C
S -1 S -1 S
$o p e n . i s e m p t y () = = f a l s e$ ，从 $o p e n$ 中选择A。

A不是目标结点，生成子节点S、G(11)，S在closed中不插入open,G不在closed和open中，因此插入open，并进行排序。 $open=\{B,G,C\},closed=\{S,A\}$

A S B G C
S -1 S A S
$o p e n . i s e m p t y () = = f a l s e$ ，从 $o p e n$ 中选择B。

B不是目标节点，生成子节点G，G在open表中，且g(G in open)=11

g(G) = 10, g(G in open)>g(G)，所以需要更新open表中的G，并进行排序。

$open=\{G,C\},closed=\{S,A,B\}$

A S B G C
S -1 S B S
$o p e n . i s e m p t y () = = f a l s e$ ，从 $o p e n$ 中选择G。

G是目标节点，通过测试，返回路径：S->B->G

A	S	B	G	C
S	-1	S	-1	S

A	S	B	G	C
S	-1	S	A	S

A	S	B	G	C
S	-1	S	B	S

代码实现

bool list[20];
vector<node> openList;
bool closeList[20];
int parent[20];
void UCS(int goal,node &src,Graph &graph)
{
    openList.push_back(src);
    list[src.name]=true;
    while (!openList.empty())
    {
        /********** Begin **********/
        sort(openList.begin(), openList.end());
		node curr = openList.front();
		closeList[curr.name] = true;
        if(curr.name==goal) {return;}
        else{
            for(int i=0;i<=5;i++)
            {
                if((graph.getEdge(curr.name,i)!=-1) && (closeList[i]==false) && (i!=parent[curr.name])  )
                {
                    node chld(i,curr.g+graph.getEdge(curr.name,i),h[i]);
                    if(list[i]==true)
                    {
                    	int Gopen = 0;
                    	//寻找到openList中的该点
						for(int j=0;j<openList.size();j++)
						{
							if(openList[j].name==i)
							{
								gpen = openList[j].g;
							}
						 } 
						//计算新的值
						int gnew = 0;
						int pa = parent[i];
						//寻找closeList中的父亲
						gnew = curr.g+graph.getEdge(curr.name,i);
						if(gnew<gopen){
							parent[i]=curr.name;
						}
					}
					else
					{
						parent[i]=curr.name;
						list[i]=true;
						node nnode = node(i,curr.g+graph.getEdge(curr.name,i));
						openList.push_back(nnode); 
					}
                }
            }
            openList.erase(openList.begin());
        }
		/********** End **********/  
    }
}