Python之建模规划篇--线性规划

基本介绍

在人们的生产实践中，经常会遇到如何利用现有资源来安排生产，以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支—数学规划，而线性规划(Linear Programming 简记LP)则是数学规划的一个重要分支。自从1947 年G. B. Dantzig 提出求解线性规划的单纯形方法以来，线性规划在理论上趋向成熟，在实用中日益广泛与深入。特别是在计算机能处理成千上万个约束条件和决策变量的线性规划问题之后，线性规划的适用领域更为广泛了，已成为现代管理中经常采用的基本方法之一。

线性规划的实例与定义

例1 某机床厂生产甲、乙两种机床，每台销售后的利润分别为4000 元与3000 元。生产甲机床需用 A、B机器加工，加工时间分别为每台 2 小时和 1 小时；生产乙机床需用 A、B、C三种机器加工，加工时间为每台各一小时。若每天可用于加工的机器时数分别为A 机器10 小时、B 机器8 小时和C 机器7 小时，问该厂应生产甲、乙机床各几台，才能使总利润最大？
上述问题的数学模型：设该厂生产x₁ 台甲机床和x₂ 乙机床时总利润最大，则 x₁,x₂应满足

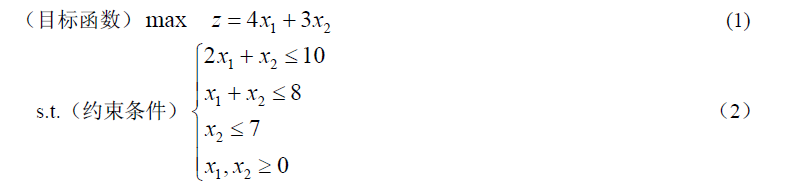
这里变量x₁, x₂ 称之为决策变量，(1)式被称为问题的目标函数，(2)中的几个不等式是问题的约束条件，记为s.t.(即subject to)。由于上面的目标函数及约束条件均为线性函数，故被称为线性规划问题。
总之，线性规划问题是在一组线性约束条件的限制下，求一线性目标函数最大或最小的问题。
在解决实际问题时，把问题归结成一个线性规划数学模型是很重要的一步，但往往也是困难的一步，模型建立得是否恰当，直接影响到求解。而选适当的决策变量，是我们建立有效模型的关键之一。

线性规划问题的解的概念

可行解 满足约束条件（4）的解 x=(x₁ ,x₂ ,… ,x_n ) ，称为线性规划问题的可行解，而使目标函数（3）达到最大值的可行解叫最优解。
可行域 所有可行解构成的集合称为问题的可行域，记为R 。

图解法简单直观，有助于了解线性规划问题求解的基本原理。我们先应用图解法来求解例1。对于每一固定的值z ，使目标函数值等于z 的点构成的直线称为目标函数等位线，当z 变动时，我们得到一族平行直线。对于例1，显然等位线越趋于右上方，其上的点具有越大的目标函数值。不难看出，本例的最优解为x* = (2,6)^T ，最优目标值z* = 26。

求解线性规划的Matlab 解法

Matlab 中线性规划的标准型为

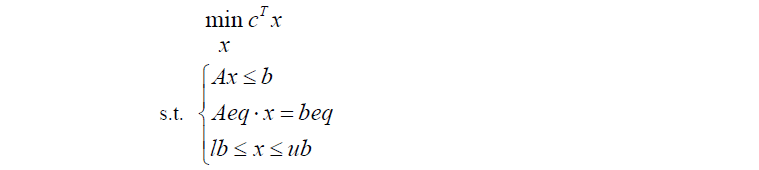
基本函数形式为 linprog(c,A,b)，它的返回值是向量x 的值。还有其它的一些函数调用形式（在 Matlab 指令窗运行 help linprog 可以看到所有的函数调用形式），如：
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
这里fval 返回目标函数的值，LB 和UB 分别是变量x 的下界和上界， x₀ 是x 的初始值，OPTIONS 是控制参数。

现在给个例子

f=[-2; -3; 5];
a=[-2,5,-1;1,3,1]; b=[-10;12];
aeq=[1,1,1];
beq=7;
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1));
x, y=-y

执行后便可得到结果

Python解法

Python Scipy库实现

同样的问题，我也可以用python实现
首先，我可以用Scipy库进行求解
大概的模板如下

# Scipy 库求解
from scipy import optimize
import numpy as np

res = 
optimize.linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIOS)
# 目标最小值
print(res.fun)
# 最优解
print(rea.x)

如果针对上面的那题,他的正确解法应该是

from scipy import optimize
import numpy as np
c = np.array([2,3,-5])
A = np.array([[-2,5,-1],[1,3,1]])
B = np.array([-10,12])
Aeq = np.array([[1,1,1]])
Beq = np.array([7])

res = optimize.linprog(-c,A,B,Aeq,Beq)
print(res)

会出现以下结果

Python plup库实现

除此之外,还可以利用plup库求解

# pulp库求解
import pulp
# 目标函数的系数
z = [2,3,1]
#约束
a = [[1,4,2],[3,2,0]]
b = [8, 6]
#确定最大化最小化问题，最大化只要把Min改成Max即可
m = pulp.LpProblem(sense=pulp.LpMinimize)
#定义三个变量放到列表中
x = [pulp.LpVariable(f'x{i}', lowBound=0) for i in [1,2,3]]
#定义目标函数，lpDot可以将两个列表的对应位相乘再加和
#相当于z[0]*x[0]+z[1]*x[1]+z[2]*x[2]
m += pulp.lpDot(z, x)
#设置约束条件
for i in range(len(a)):
    m += (pulp.lpDot(a[i], x) >= b[i])
#求解
m.solve()
#输出结果
print(f'优化结果：{pulp.value(m.objective)}')
print(f'参数取值：{[pulp.value(var) for var in x]}')

依然可以得到正确的结果

一个十分有趣的例子

最后我看到了一个十分十分有趣的例子,是二维的线性规划问题,依旧用python实现

import pulp
import numpy as np
from pprint import pprint
def transportation_problem(costs, x_max, y_max):
    row = len(costs)
    col = len(costs[0])
    prob = pulp.LpProblem('Transportation Problem',sense = pulp.LpMaximize)
    var = [[pulp.LpVariable(f'x{i}{j}', lowBound=0,cat=pulp.LpInteger) for j in range(col)] for i in range(row)]
    flatten = lambda x: [y for l in x for y in flatten(l)] if type(x) is list else [x]
    prob += pulp.lpDot(flatten(var), costs.flatten())
    for i in range(row):
        prob += (pulp.lpSum(var[i]) <= x_max[i])
    for j in range(col):
        prob += (pulp.lpSum([var[i][j] for i in range(row)]) <= y_max[j])
#     print(prob)
    prob.solve()
    return {'objective':pulp.value(prob.objective),'var':[[pulp.value(var[i][j])for j in range(col)]for i in range(row)]}

if __name__ == '__main__':
    costs = np.array([[500, 550, 630, 1000, 800, 700],
                        [800, 700, 600, 950, 900, 930],
                        [1000, 960, 840, 650, 600, 700],
                        [1200, 1040, 980, 860, 880, 780]])
    max_plant = [76, 88, 96, 40]
    max_cultivation = [42, 56, 44, 39, 60, 59]
    res = transportation_problem(costs, max_plant,
    max_cultivation)
    print(f'最大值为{res["objective"]}')
    print('各变量的取值为：')
    pprint(res['var'])

就这样,我们可以得到最优方案

插一句,如果你把prob打印出来,你可以看到太他的内部是这样的

每日一句
Giving is a reward in itself.(给予本身就是一个奖赏)