衡量特征变量对模型的贡献度，试下这类数据探索交叉分析方法

在日常建模过程中，针对模型训练前的样本探索分析，我们往往需要投入一定的时间，其主要目的一方面是了解样本数据的整体分布情况，另一方面是为了探索分析各特征字段的属性，例如样本数量、特征数量、特征类型、缺失占比等。当然，样本的描述性统计分析过程，是数据分析最简单也是非常有必要的环节。但是，在实际建模场景中，对于有监督模型的构建，除了要熟悉特征数据的分布情况之外，还需要对特征变量与目标变量的关系进行交叉分析，这样可以便于了解特征字段对模型的潜在贡献价值，从而实现特征变量筛选与模型性能优化。
对于特征变量X与目标变量Y的交叉探索分析，由于字段从分布类型可以划分为连续型与离散型，且离散型又可以进一步区分二分类与多分类，因此在本文将根据这些细分维度，来全面介绍特征变量与目标字段之间关系的分析思路，具体包括以下几种情况：
（1）目标变量为连续型：
Case1：离散变量X与连续变量Y；
Case2：连续变量X与连续变量Y；
Case3：时间变量X与连续变量Y。

（2）目标变量为离散型：
Case1：离散变量X与二分类变量Y；
Case2：连续变量X与二分类变量Y；
Case3：离散变量X与多分类变量Y；
Case4：离散变量X与多分类变量Y。

为了实现以上各场景下的X与Y的交叉分析，我们围绕具体的测试样本数据，来依次介绍各case的分析过程，同时会结合可视化形式对相关结果进行展示。本文选取的数据包含100条样本和6个字段，部分样例如图1所示。其中，ID为样本主键，X1、X2为特征变量（X1为离散型、X2为连续型），Y1、Y2、Y3为目标变量（Y1为连续型、Y2为二分类型、Y3为多分类型）。
​

                                                                 图1 样本数据样例

以上对样本各字段类型的设置，是为了满足前边各case场景下的数据类型要求，以实现相关特征字段之间的联系，接下来我们依次对其进行介绍。
1、离散变量X与连续变量Y
离散型变量X、连续型变量Y分别选取图1中的字段X1、Y1，二者的关系，可以整体分析每个类别变量与数值标签之间的分布关系，具体了解每个类别情况下的标签变量均值，可通过pandas方法绘制数据分布图，而且也可以考虑采用boxplot方法来分析。以上分析思路的具体实现过程如图2所示，输出的可视化结果分别如图3、图4所示。
​
图2 离散型X与连续型Y分析
​

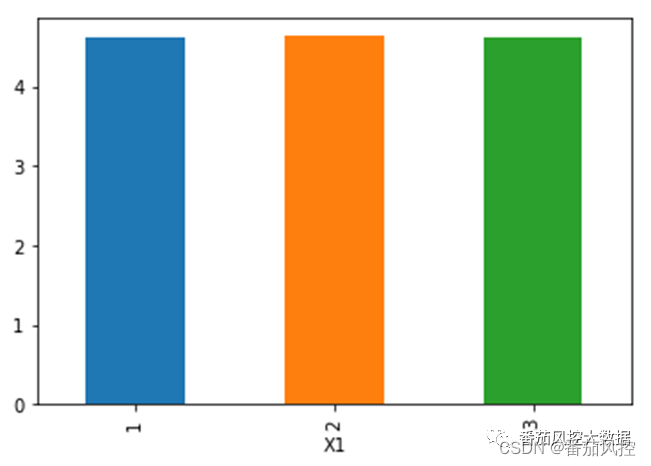
                                              图3 离散型X与连续型Y结果（pandas）

​

图4 离散型X与连续型Y结果（boxplot）

通过以上可视化结果可以得知，特征变量X1各取值（1、2、3）对应目标变量Y的均值比较接近，尤其是X1为1和2时，二者标签的中位数分布也非常接近，尽管X1为3时的中位数较低，但整体上特征X1对标签Y1没有明显的区分度。

2、连续变量X与连续变量Y
连续型变量X、连续型变量Y分别选取图1中的字段X2、Y1，可以通过常见的person相关系数来量化分析二者的关系。同时也可以考虑采用scatter或regplot绘图方法来进行可视化分析。以上分析思路的具体实现过程如图5所示，输出的可视化结果分别如图6、图7所示。
​
图5 离散型X与连续型Y分析

​
图6 连续型X与连续型Y结果（scatter）

​

图7 连续型X与连续型Y结果（regplot）

图5的变量相关性分析，字段X2与Y1的系数分布为二维矩阵类型，在本文测试数据情形下的结果是0.013591，相关性系数数值较低，说明二者相关程度很弱。通过scatter和regplot的可视化绘图结果可以直观再次确认，字段X2与Y1的变化趋势没有明显的联系。

3、时间变量X与连续变量Y
由于本文数据没有时间型变量，为了更好的展示时序数据分布，这里选取样本数据的索引index作为时间变量X，而连续型变量Y为图1中的字段Y1。针对时间变量X与连续变量Y的分布，可以采用plot来绘制可视化结果。以上分析思路的具体实现过程如图8所示，输出的可视化结果分别如图9所示。

图8 时间型X与连续型Y分析

​
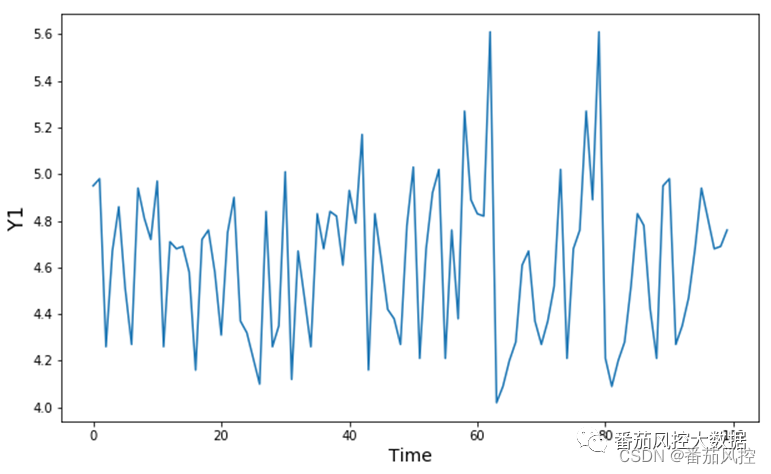
图9 时间型X与连续型Y结果

从上图的可视化结果可以看出，时间型变量X（Time）与连续型变量Y1的变化趋势整体表现平稳，但Time在60~80之间稍有明显波动，在实际场景中，可以重点研究时间型字段的具体分布。

4、离散变量X与二分类变量Y
离散型变量X、二分类型变量Y分别选取图1中的字段X1、Y2，一方面可以通过groupby方式来分组了解特征取值的标签分布，另一方面也可以考虑将二者的数据分布通过boxplot绘图方式来展示可视化结果。以上分析思路的具体实现过程如图10所示，输出的可视化结果分别如图11所示。
​
图10 离散型X与二分类型Y分析

​
图11 离散型X与二分类型Y结果

图10针对特征变量X1取值（1、2、3）的标签均值分布，其结果依次为0.50、0.48、0.45，数值整体上比较接近。因此，在图11的可视化分布上也非常类似，主要体现在特征X1各取值情况下的最大值（1）与最小值（0）是完全一致的，但X1为1的中位数分布较为均匀，而X1为2或3时比较偏离中部位置。

5、连续变量X与二分类变量Y
连续型变量X、二分类型变量Y分别选取图1中的字段X2、Y2，这里可以按照上个case（离散型X与二分类型Y）的分析思路来探索，但这里需要注意的是，为了使boxplot可视化结果更有可读性，图表的横坐标X设置为目标变量Y2。以上分析思路的具体实现过程如图12所示，输出的可视化结果分别如图13所示。
​
图12 连续型X与二分类型Y分析

​

                                                       图13 连续型X与二分类型Y结果

图12针对二分类型标签Y2取值（0、1）的特征变量X2均值分布，其结果依次为557、552，数值差异并非很明显。同时，从对应图13的可视化结果也可以得到直观了解，Y2在0和1两种取值情况下的分布比较接近。

6、离散变量X与多分类变量Y
离散型变量X、多分类型变量Y分别选取图1中的字段X1、Y3，对于二者的关系可以通过countplot方式来展示直方图进行分析。以上分析思路的具体实现过程如图14所示，输出的可视化结果分别如图15所示。
​

                                                       图14 离散型X与多分类型Y分析

​
）
图15 离散型X与多分类型Y结果
从上图的可视化结果可以得知，对于多分类标签Y3的取值情况（1、2、3、4），对应离散型变量X1的数量汇总count分布上有一定差异，各组特点较为明显。

7、连续变量X与多分类变量Y
连续型变量X、多分类型变量Y分别选取图1中的字段X2、Y3，二者关系可以通过boxplot方式绘制其数据分布。以上分析思路的具体实现过程如图16所示，输出的可视化结果分别如图17所示。
​

                                                       图16 连续型X与多分类型Y分析

​

                                                         图17 连续型X与多分类型Y结果

从上图的可视化结果可以得知，对于多分类标签Y3的取值情况（1、2、3、4），对应连续型变量X2的分布差异较为明显，区分度表现较好。
综合以上内容，我们从目标变量为连续型与离散型两个场景，分别从离散变量X与连续变量Y、连续变量X与连续变量Y、时间变量X与连续变量Y、离散变量X与二分类变量Y、连续变量X与二分类变量Y、离散变量X与多分类变量Y、离散变量X与多分类变量Y共7个case分析了特征变量与目标字段之间的关系，同时采用相关绘图方法实现了可视化分析与解读。
本文的介绍内容，对于数据建模场景中特征与标签的交叉探索分析，是非常重要的环节，为特征字段筛选与模型性能优化提供很的的信息参考价值。
为了便于大家对以上特征交叉探索分析的进一步了解与熟悉，本文额外附带了与以上内容同步的python代码与样本数据，详情请移至知识星球查看相关内容。

…

~原创文章