四十七、Fluent近壁面处理

0. 前言

今天这篇文章，我们介绍一下近壁面处理的方式来求解湍流壁面物理规律。

前文四十五、四十六及本文四十七这三篇文章可以说是非常详细而系统的把壁面函数及相关理论全都介绍了一遍，大家可以参考进行设置。也希望大家能多多转发，点赞呀，感谢感谢

1. 近壁面处理

前面介绍了壁面函数的由来及相关的理论，我们已经知道，壁面函数只考虑了对数律的适用范围，而完全忽略了粘性底层的影响。

但是对于一些工况，我们所关注的点就是粘性底层物理量的规律，比如边界层分离现象，这时候壁面函数就不再适用了。参考文章四十六Fluent壁面函数的选取依据，只要有以下的情况，壁面函数就不可用了。很低的雷诺数流动，如毛细现象
壁面相变问题，如壁面沸腾现象
大压力梯度导致的边界层分离现象
依靠体积力驱动的流动，如自然对流，浮力等
对于3D模型，边界层歪斜度较大也不适用壁面函数
那应该如何处理呢？？？
我们只能回到最初的想法----对边界层网格进行加密，同时对湍流模型进行修正，使其能够对粘性底层进行求解。

2. Enhanced Wall Treatment

增强近壁面处理方式将两层模型和增强的壁面函数结合，对于壁面粗网格（y+>15，完全湍流区）和精细网格（y+≈1，粘性底层）都不会产生太大的误差。

2.1 Two-Layer Model

两层模型将边界层划分为粘性底层和完全湍流层，两层的分界线用雷诺数Rey区分

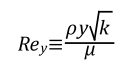
y为网格中心到壁面的距离。
如果Rey<200，流体处于粘性底层区，使用Wolfstein一方程求解；如果Rey>200，流体处于完全湍流区，使用k-e模型或者雷诺应力模型求解。

增强的壁面处理（Enhanced Wall Treatment）能够在整个近壁区域（即粘性底层，缓冲区和完全湍流外区域）都适用，这种方式将线性律和对数律组合在一起，从而扩大模型的使用范围。

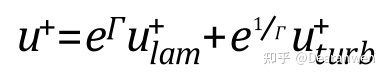
2.2 混合函数

其中a=0.01，b=5。
当y+很小约等于1时流体处在粘性底层，流动规律符合线性律。此时混合函数：

同理y+≈15时，流体处在完全湍流区，流动规律符合对数律。此时混合函数：

从上能够看出，Enhanced Wall Treatment能够自动根据y+的值选择不同的湍流规律，因此Enhanced Wall Treatment适用于整个湍流区域，对y+不敏感。但是如果想要研究粘性底层，还是必须要将网格划分的足够细才可以。

注：
Enhanced Wall Treatment适用于所有基于e方程的湍流模型，如k-e模型，雷诺应力模型

2.3 壁面函数VS Enhanced Wall Treatment

选用文章四十五的案例，将Standard Wall Functions、Scalable Wall Functions和 Enhanced Wall Treatment进行对比，一侧y+=1，另一侧y+>15。

可以看出，Scalable Wall Functions和 Enhanced Wall Treatment的速度曲线明显比较接近，而Standard Wall Functions在y+=1一侧，出现了较大的误差。

3. Menter-Lechner treatment

有两种方式可以用来求解壁面边界层流动，分别是壁面函数法和低雷诺数模型。

壁面函数法文章四十五、四十六进行了详细介绍，它对y+要求很严格；而所谓低雷诺数模型，就是考虑到粘性底层的流动，要求y+<1，如果y+>=1，则求解不准确。

这两种模型对于y+要求苛刻，那么有没有一种模型能够对y+不敏感呢？？Menter-Lechner treatment就是这样一种模型。当壁面网格很细，使用低雷诺模型，当壁面网格较粗时，使用壁面函数。

实际上Enhanced Wall Treatment对y+也不敏感。

上文提到Enhanced Wall Treatment依据Rey是否大于200将流动区域划分为粘性底层和完全湍流层。这种划分方法存在一些问题：
1）当湍流强度较低时，流体距离壁面较远，Rey仍然小于200。但Enhanced Wall Treatment方法仍然将这部分流体划分为粘性底层，这显然不正确。
2）当流动处于粘性底层时，一方程用于求解湍流规律，但一方程求解非平衡现象存在问题。

Menter-Lechner treatment方法就是为了解决Enhanced Wall Treatment在低雷诺数时出现的问题。门特-莱克纳近壁处理在湍流动能的输运方程中增加一个源项

式中，Snear-wall仅作用在粘性低层中，用于代替低雷诺数模型。在对数律区域内，Snear-wall自动变为零。


注：
Menter-Lechner treatment方法可用于standard、realizable和RNG k-e湍流模型

4. ω方程--y+不敏感近壁面处理

所有ω方程都可以对粘性底层进行积分，而不需要像e方程那样采用两层模型的方法。因此ω方程默认的就是将粘性底层和对数律层的规律通过混合函数进行混合，从而达到对y+不敏感的近壁面处理。

ω方程将粘性底层与对数律的混合方法与Enhanced Wall Treatment相同，默认对于近壁面的处理就是这种方式。

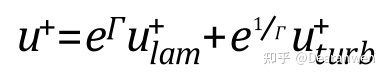
混合函数

因此对于所有基于ω方程的湍流模型，都不需要考虑近壁面的处理方式，同样也不需要考虑壁面函数。

如k-ω模型，Transition k-kl-omega ( 3 eqn )模型等。Fluent中基于ω方程的湍流模型界面都没有壁面函数的选项。

5. LES Near-Wall Treatment

对于大涡模型LES，Fluent也提供了一种近壁面处理方式LES Near-Wall Treatment。这种处理方式由Werner和Wengle提出，因此也被称为werner-wengle wall function。

这种近壁面处理方式并不能通过界面打开。需要在打开LES模型的前提下，在控制面板输入文本命令：define/models/viscous/near-wall-treatment/werner-wengle-wall-fn?


注：
LES大涡模型在三维模型可以在Fluent湍流模型界面打开，但是二维模型时，需要输入文本命令才能打开LES模型。
文本命令：(rpsetvar 'les-2d? #t)

6. Fluent壁面处理推荐设置

总结：对于k-e模型和雷诺应力模型，可以选择壁面函数，也可以设置近壁面处理；
对于k-ω模型和Spalart-Allmaras，默认方式就是y+不敏感的近壁面处理方式，不需要进行任何设置。

大家选择壁面函数时，推荐使用以下设置：

1) 对于基于e方程的模型，直接使用Menter-Lechner(ML- e)或者Enhanced Wall Treatment。尽量不使用壁面函数。

2) 对于e方程模型，如果必须使用壁面函数，那就选择scalable wall functions

3) 对于k-ω模型，使用默认的y+不敏感的壁面处理方式。实际上所有基于ω方程的湍流模型都是如此，不需要进行任何壁面函数设置。

4) 对于Spalart-Allmaras模型，使用默认的y+不敏感的壁面处理方式，也不需要进行任何壁面函数设置。



点赞+转发+在看，让更多的人看到这篇文章，是我更新的动力，大家多多支持啊。

原文链接：

四十七、Fluent近壁面处理对于k-e模型和雷诺应力模型，可以选择壁面函数，也可以设置近壁面处理；对于k-ω模型和Spalart-Allmaras，默认方式就是y+不敏感的近壁面处理方式，不需要进行任何设置。https://mp.weixin.qq.com/s/3CGFZPJFAMVTY4hIiMH2nA