《数据结构》天勤和王道 第五章 树

天勤部分

1. 树的基础知识

树是一种递归定义的数据结构。递归特性：当前每一层都跟上一层有类似的结构，每一个子结构跟其父结构都类似。

1.1 结点的度

1.2 树的度

所有结点中最大的分支数就是树的度。

1.3 叶子结点

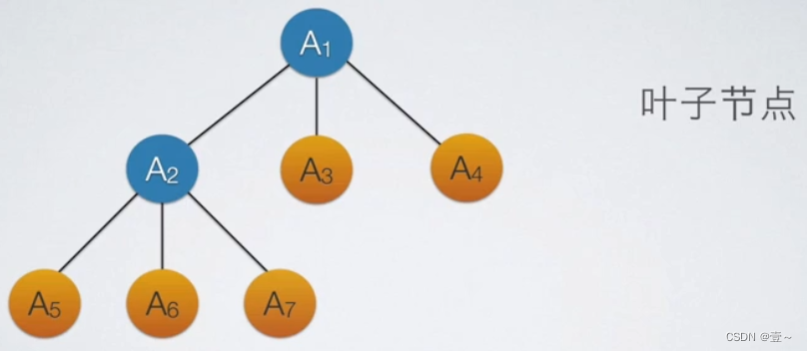
度为0的结点就是叶子结点。

1.4 双亲结点、孩子结点、祖先结点和子孙结点

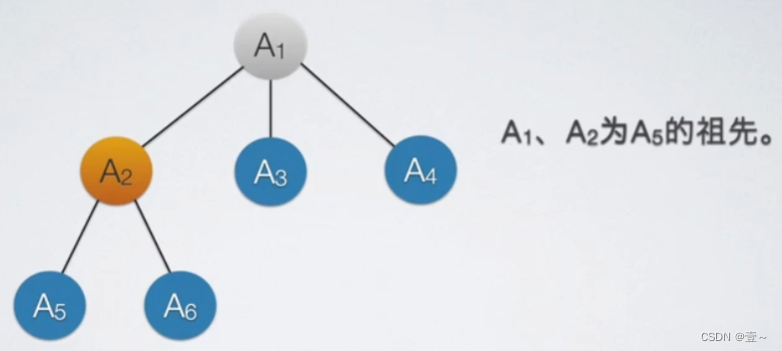
1.5 兄弟结点和堂兄弟结点

1.6 高度和深度

1.7 存储结构

这部分直接看下面王道的“10. 树的存储结构”。

2. 二叉树的逻辑结构和存储结构

2.1 性质

2.2 叶子结点数=双分支结点数+1的灵活运用

当求一棵树中的空指针个数等时，我们可以先在每个结点上填充上空指针，使得每个结点的度都为2，然后就可以运用公式了。

2.3 m叉树的性质

王道部分

1. 树的定义和基本术语

2. 树的常考性质

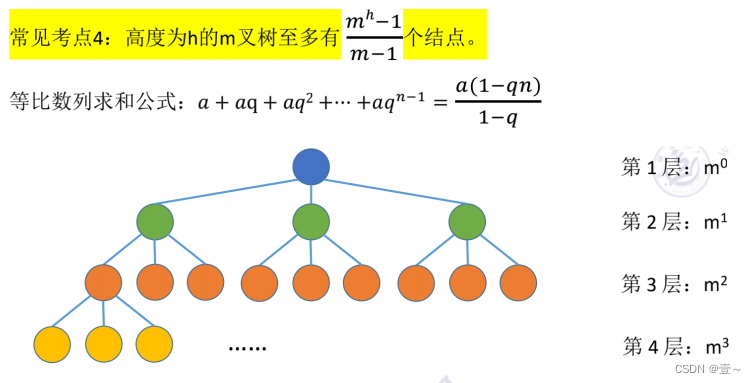
3. 二叉树的定义和基本术语

3.1 满二叉树和完全二叉树

满二叉树是一种特殊的完全二叉树。

3.2 二叉排序树

3.3 平衡二叉树

4. 二叉树的性质

4.1 二叉树的常考性质

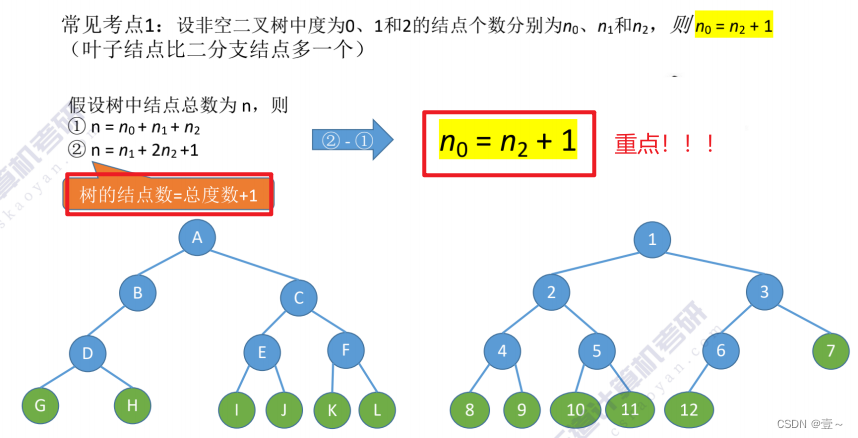
结点树=总度数+1；这的“1”表示的是根结点。

4.2 完全二叉树的常考性质

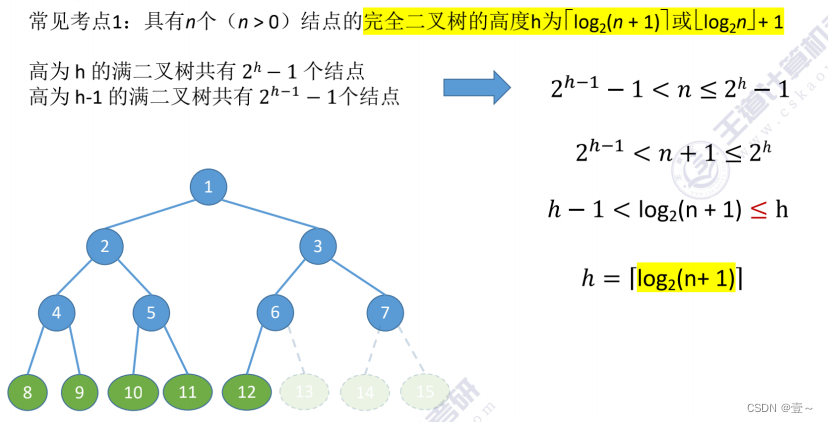
这里的 h-1<log₂ (n+1)<=h，表示的是log₂ (n+1)在 h-1 和 h 之间相差不到一的小数，由于是<=h，所以向上取整。

5. 二叉树的存储结构

5.1 顺序存储

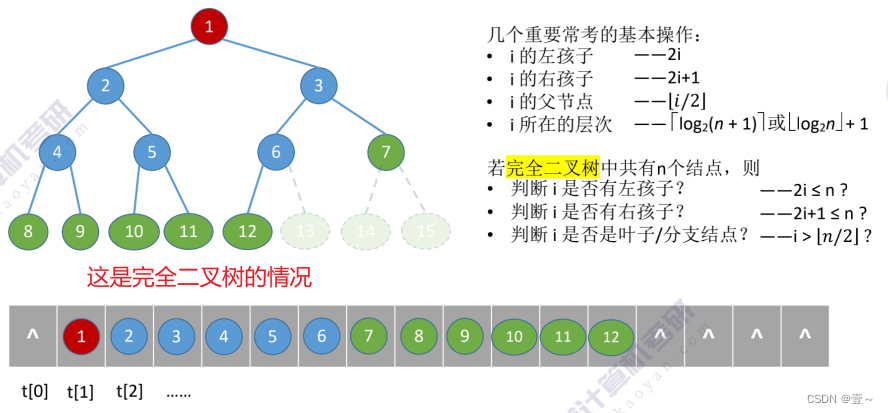
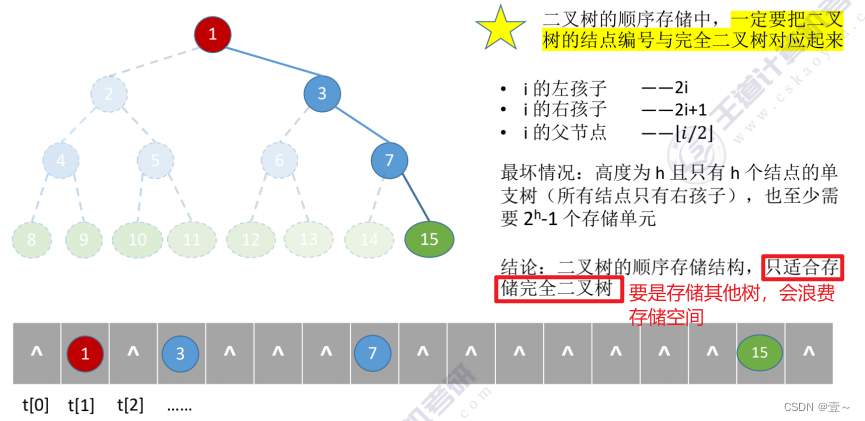
5.2 链式存储

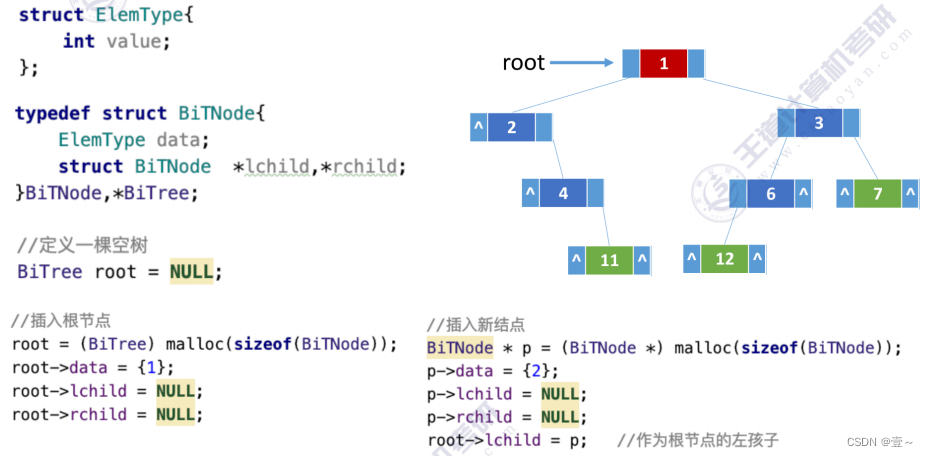
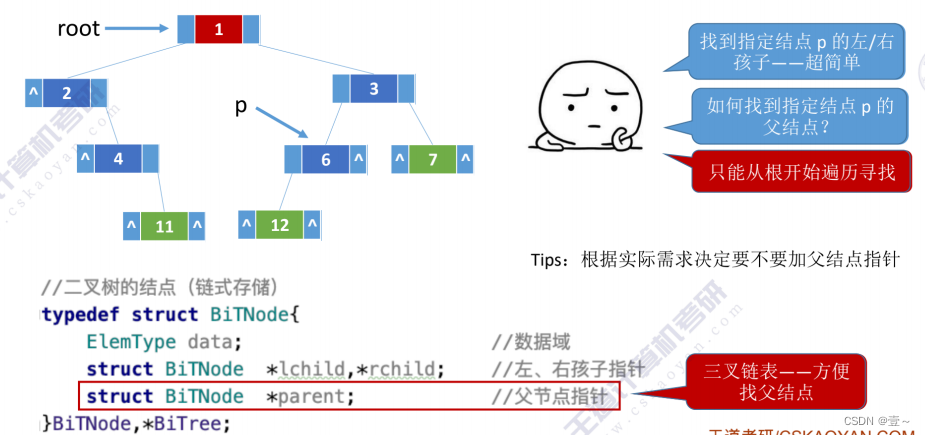
6. 二叉树的先中后序遍历

6.1 先序遍历的代码

6.2 中序遍历的代码

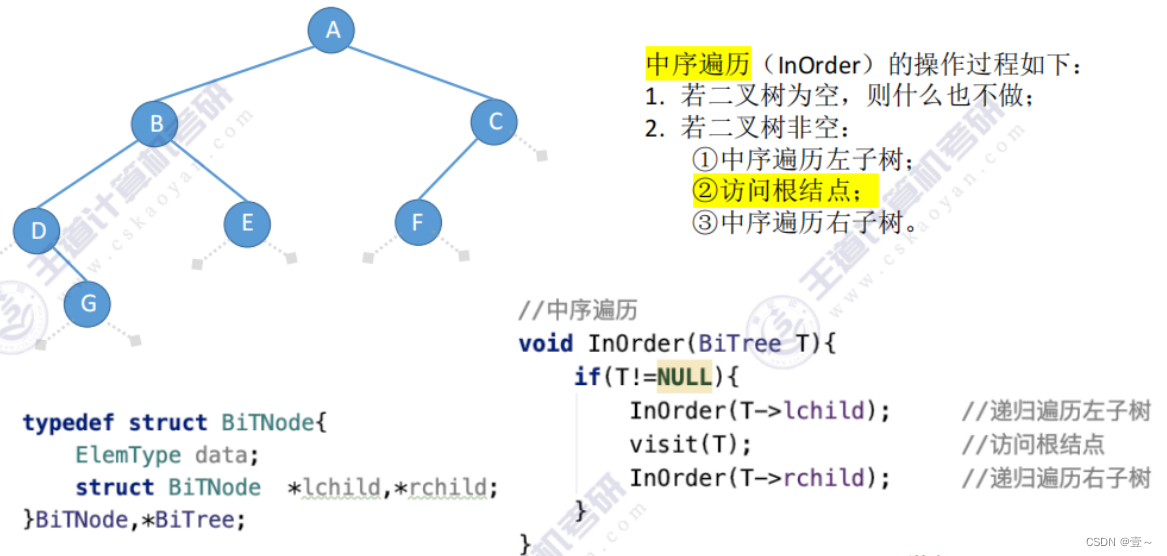
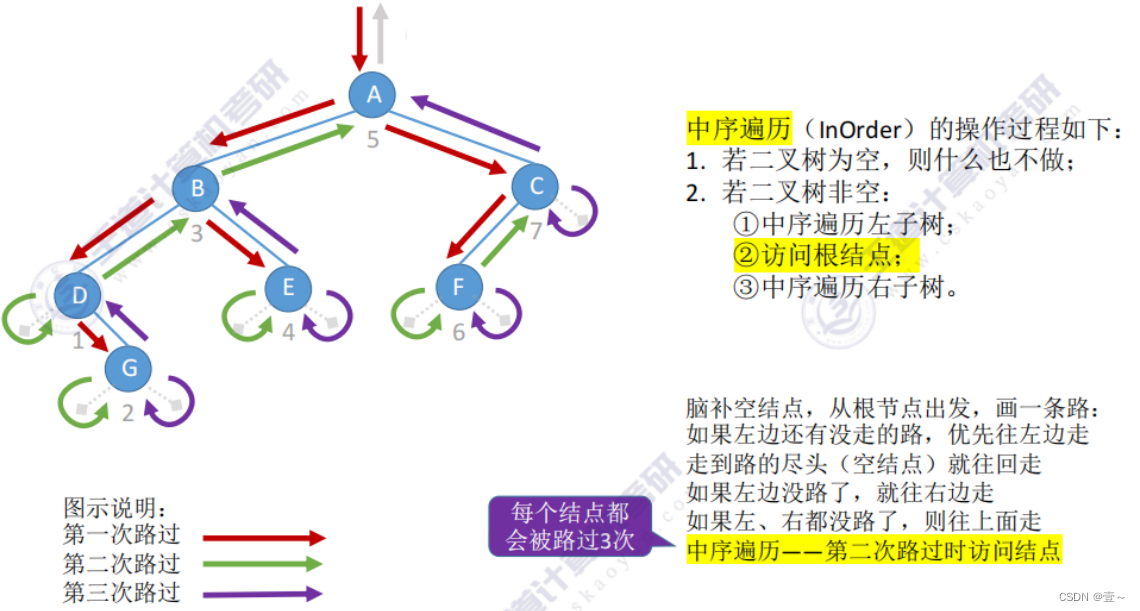
6.3 后序遍历的代码

6.4 遍历算术表达式树

7. 二叉树的层序遍历

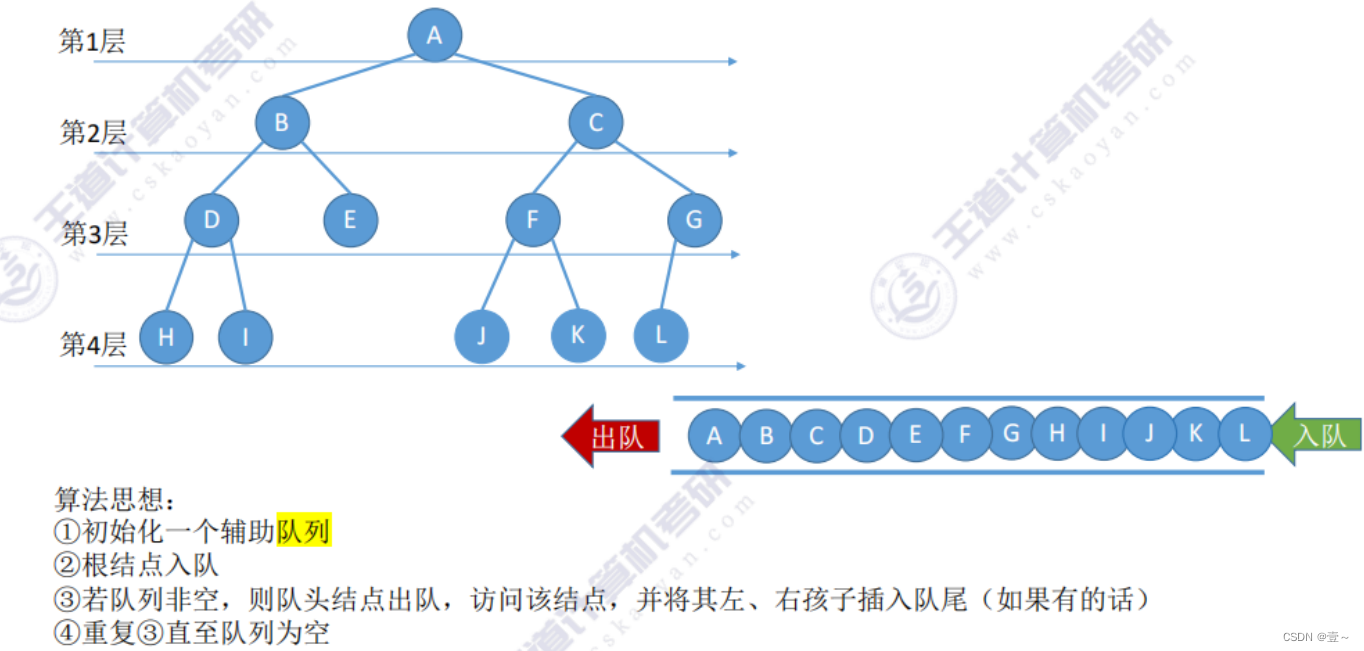
8. 由遍历序列构造二叉树

8.1 不同二叉树的遍历序列

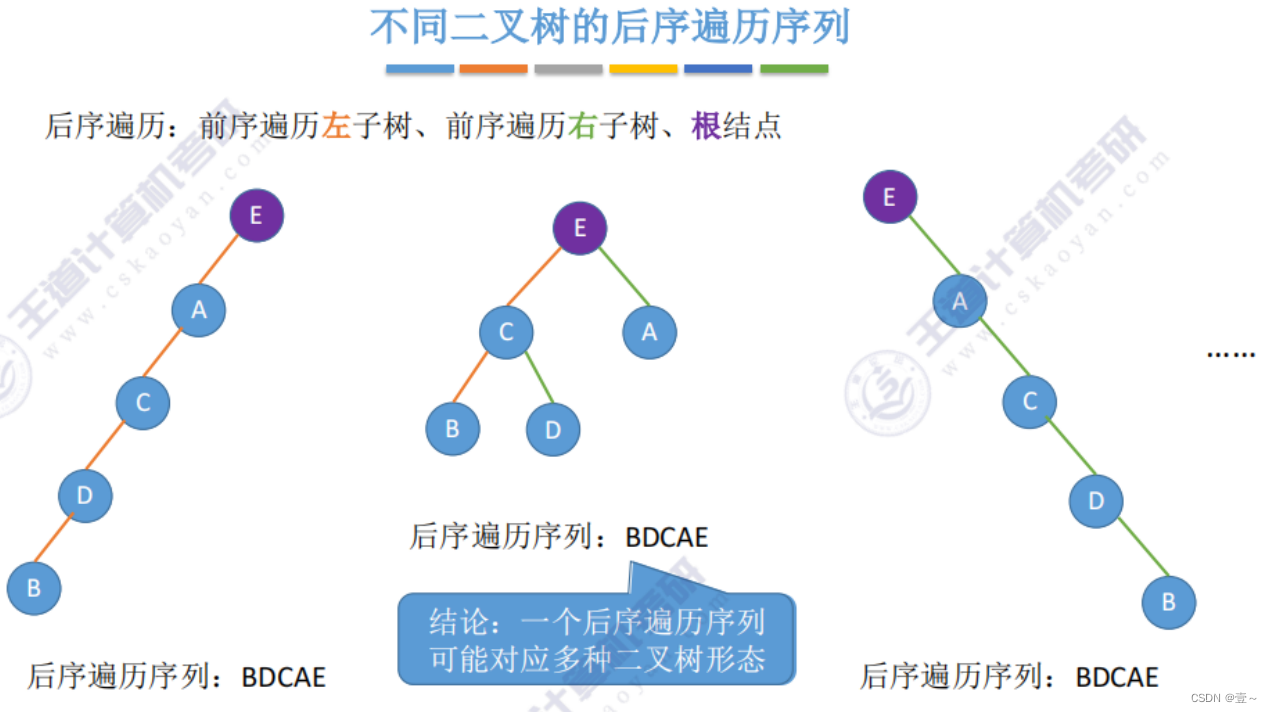
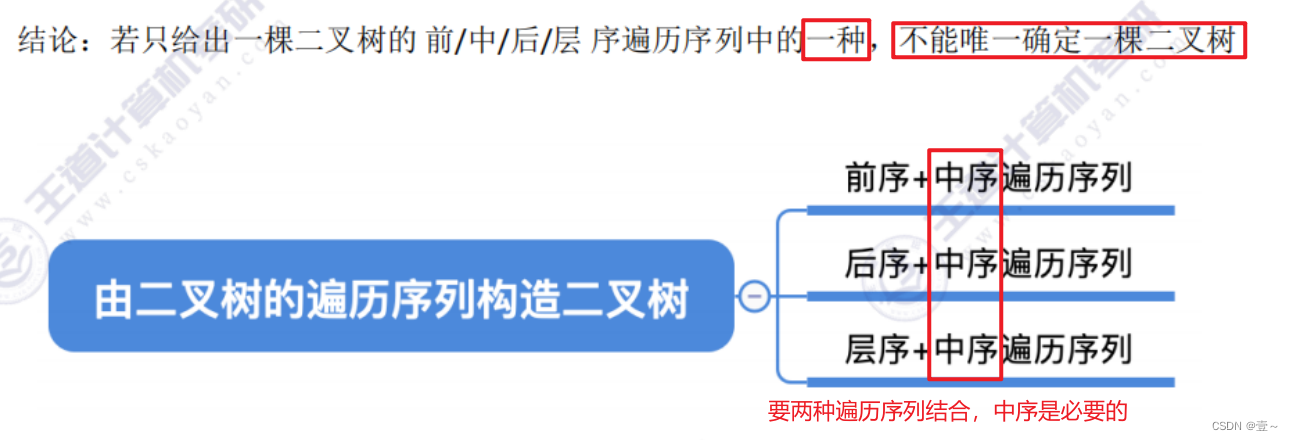
8.2 前序+中序遍历序列

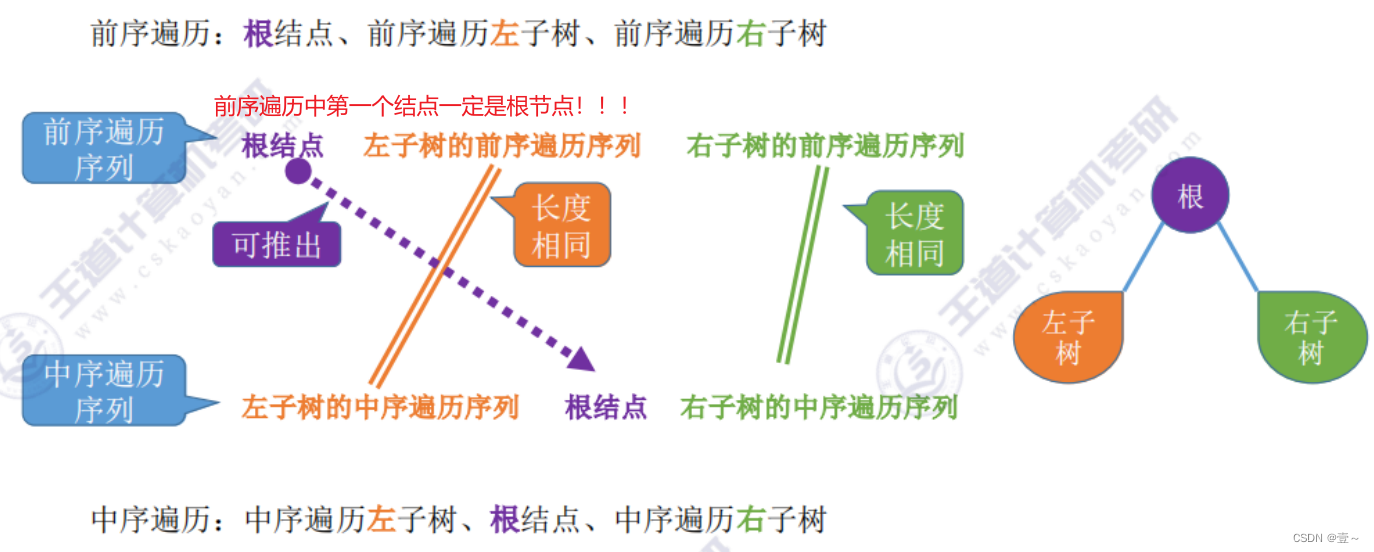
举个例子：

8.3 后序+中序遍历序列

举个例子：

8.4 层序+中序遍历

举个例子：




再举个例子：





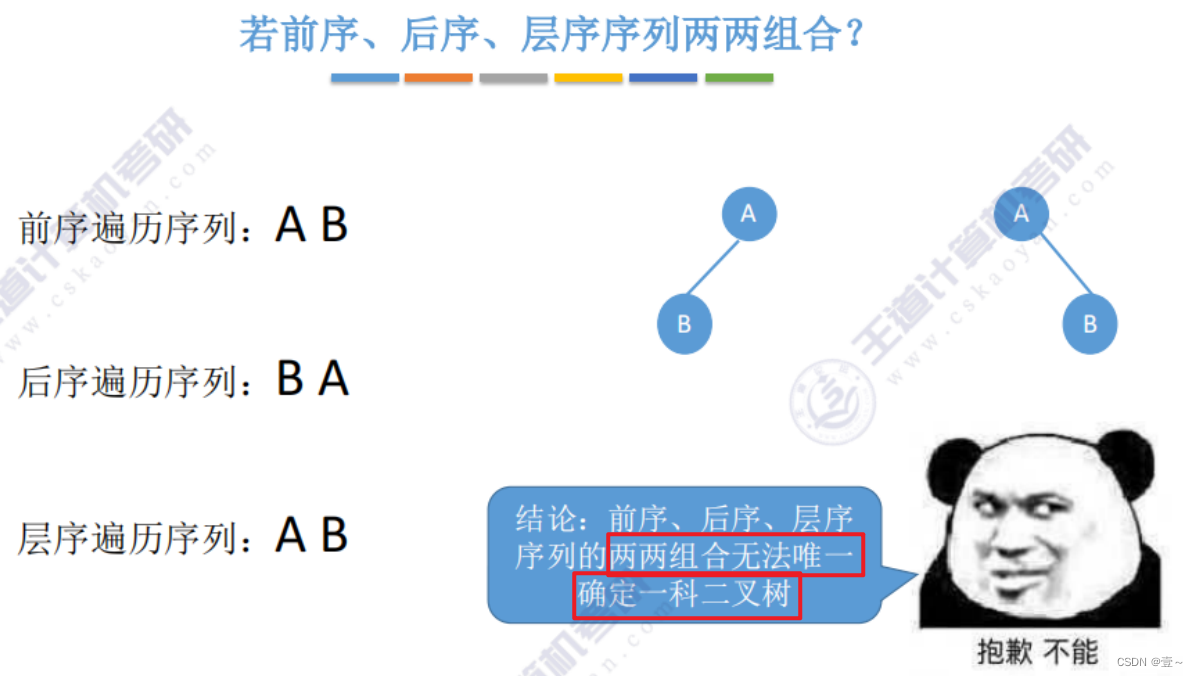
必须跟中序序列组合才能确定唯一的二叉树。

9. 线索二叉树

9.1 线索二叉树的概念

遍历二叉树是以一定的规则讲二叉树中的结点排列成一个线性序列，从而得到几种遍历序列，使得该序列中的每个结点（第一个和最后一个结点除外）都有一个直接前驱和直接后继。
这种是没有线索的时候，找遍历序列中的前驱和后继。

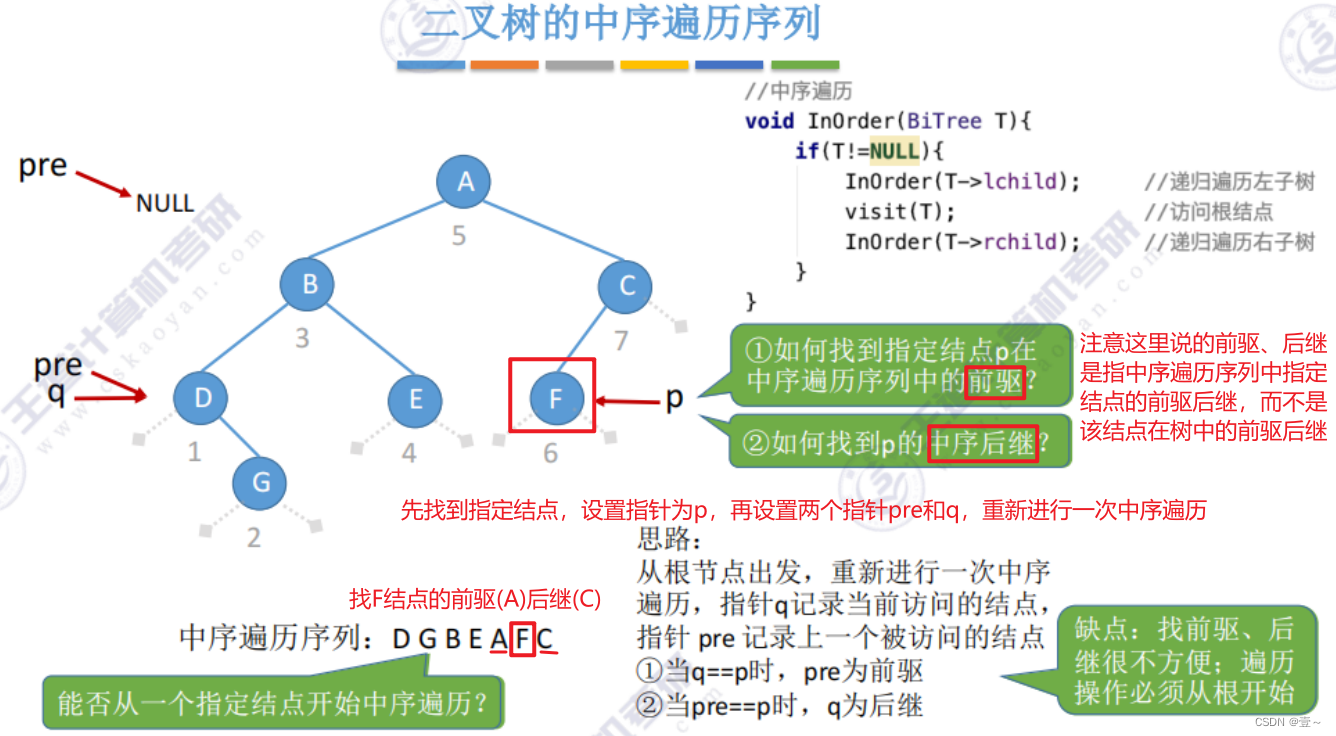
通过中序遍历，先访问D结点（visit(D)），然后继续执行下去。

9.1.1 中序线索二叉树

线索二叉树的存储结构

9.1.2 先序线索二叉树

9.1.3 后序线索二叉树

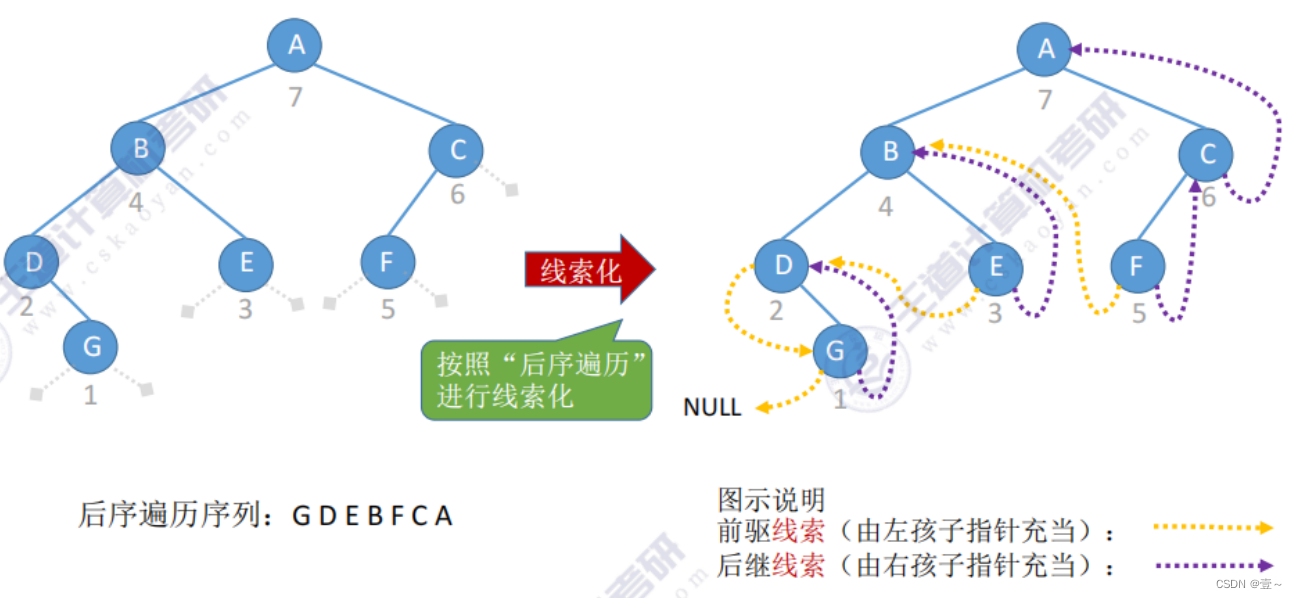
9.2 二叉树的线索化（代码实现）

9.2.1 中序线索化

9.2.2 先序线索化

9.2.3 后序线索化

9.3 线索二叉树找前驱/后继

9.3.1 中序线索二叉树找中序后继

9.3.2 中序线索二叉树找中序前驱

9.3.3 先序线索二叉树找先序后继

9.3.4 先序线索二叉树找先序前驱

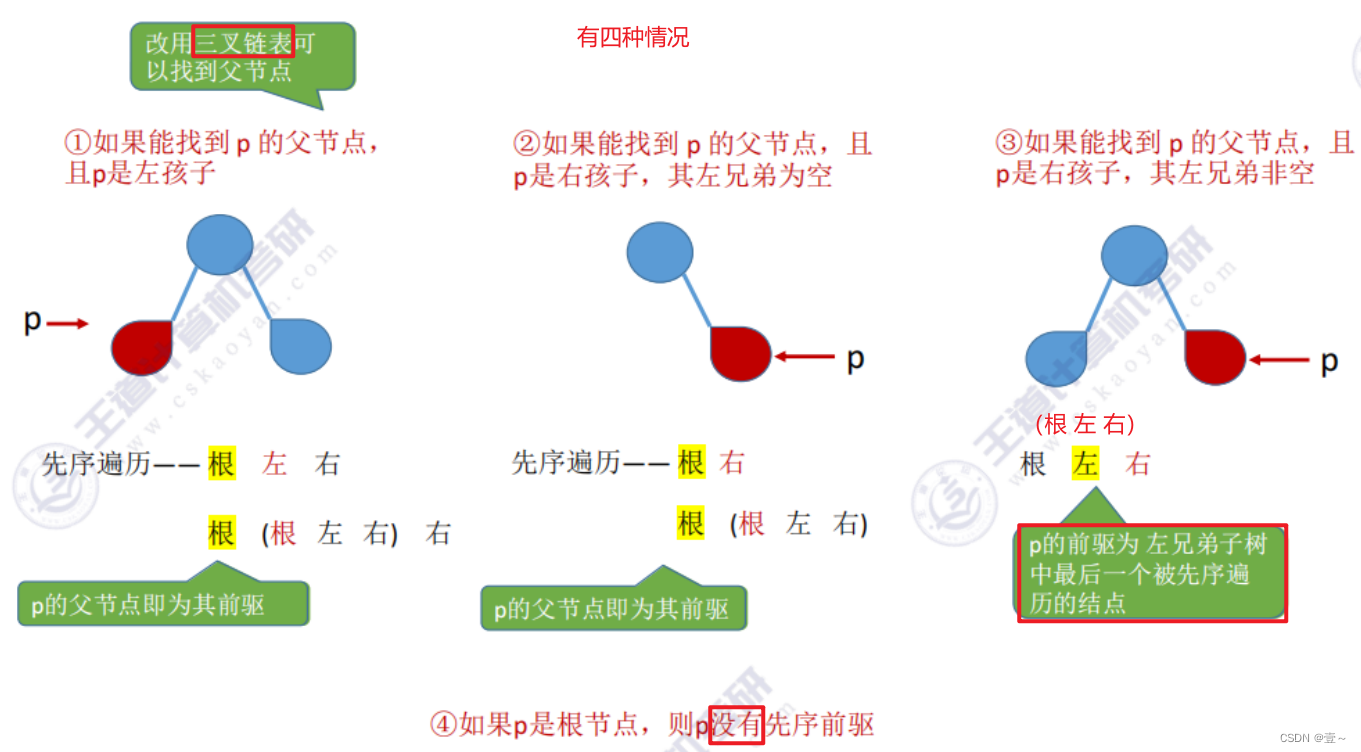
9.3.5 后序线索二叉树找后序前驱

9.3.6 后序线索二叉树找后序后继

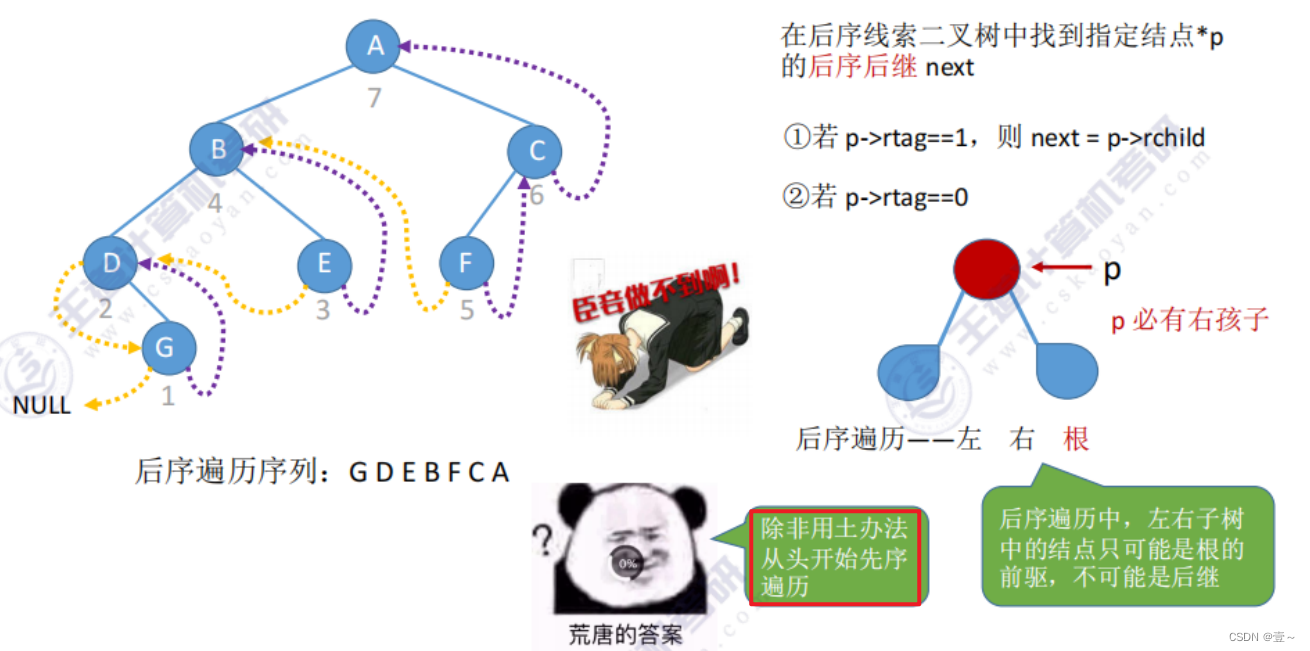
10. 树的存储结构

10.1 双亲表示法（顺序存储）

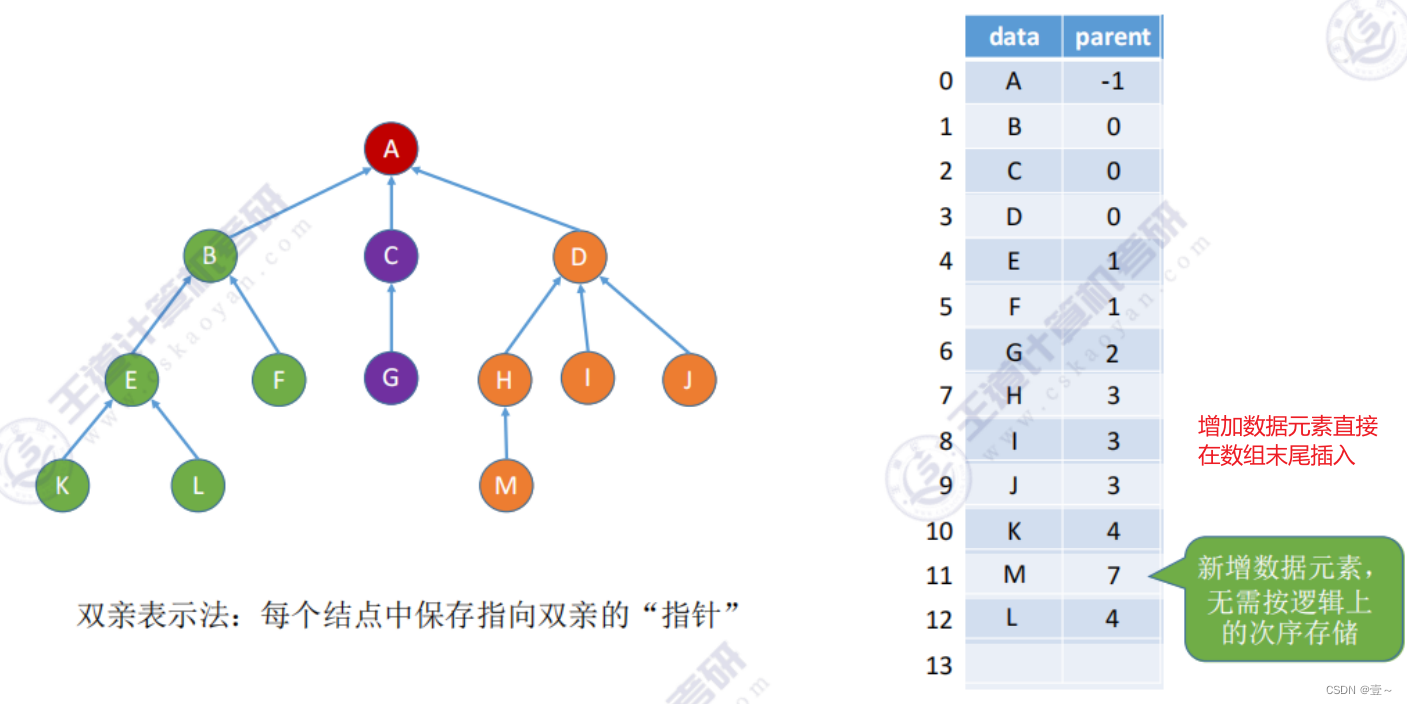
10.2 孩子表示法（顺序+链式存储）

10.3 孩子兄弟表示法（链式存储）

10.4 森林和二叉树的转换

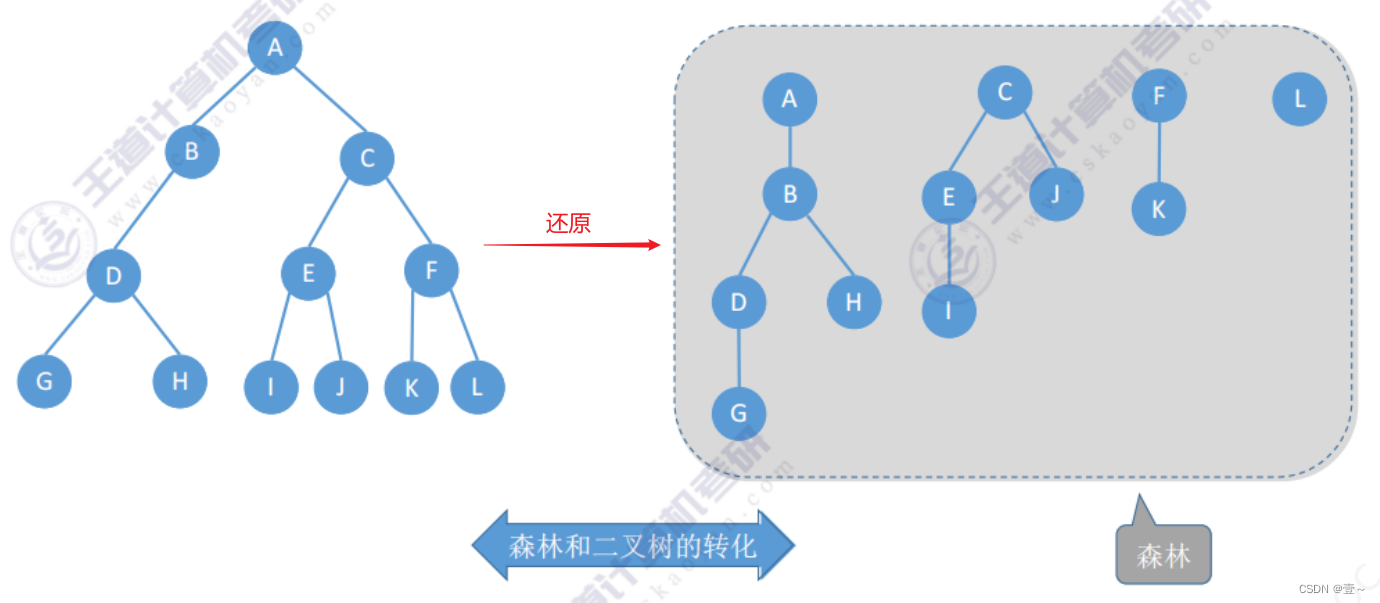
11 树、森林的遍历

11.1 树的先根遍历

11.2 树的后根遍历

11.3 树的层次遍历

11.4 森林的先序遍历

11.5 森林的中序遍历

如果考试要是考到关于遍历森林的代码的话，我们可以先转换成上述这种二叉树（即森林用二叉树来存储），然后利用我们熟悉的二叉树代码继续解决。

12. 哈夫曼树

12.1 带权路径

12.2 哈夫曼树的定义

只要是最优二叉树就是哈夫曼树。

12.3 哈夫曼树的构造

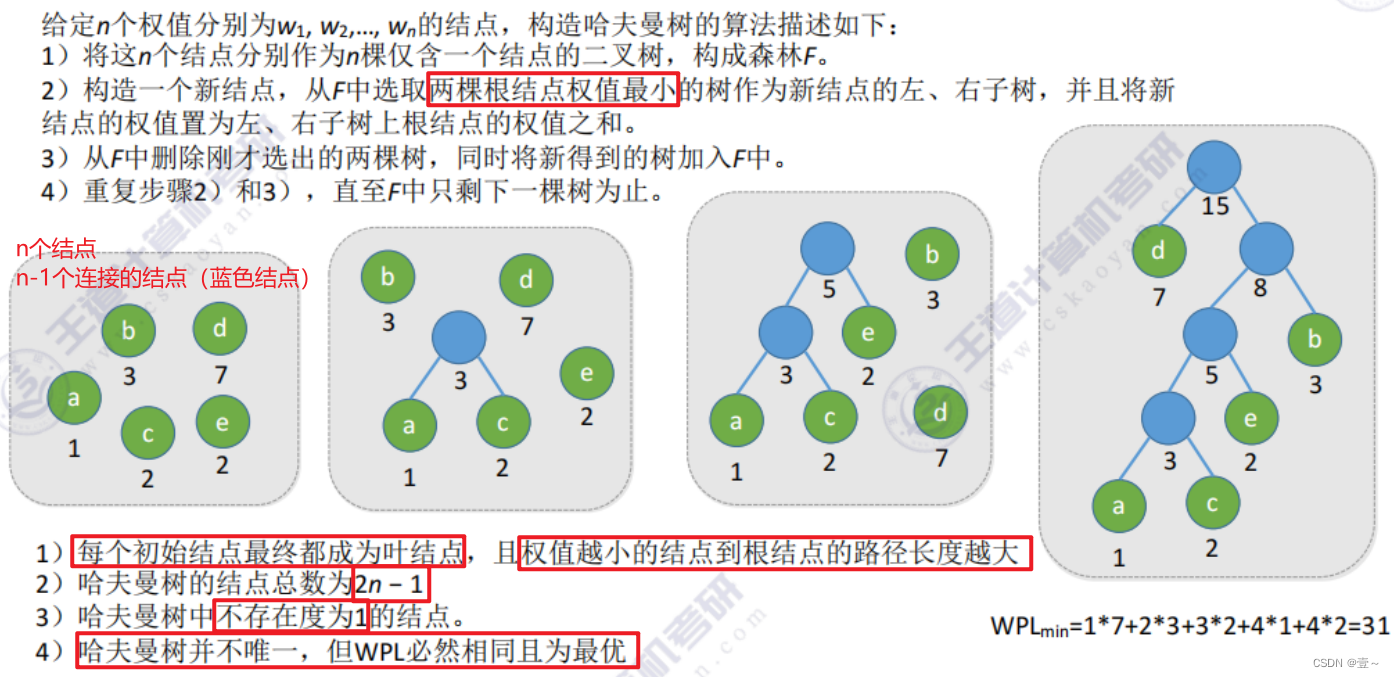
12.4 哈夫曼编码

13. 并查集（新增考点）

并查集的逻辑结构是一个集合。




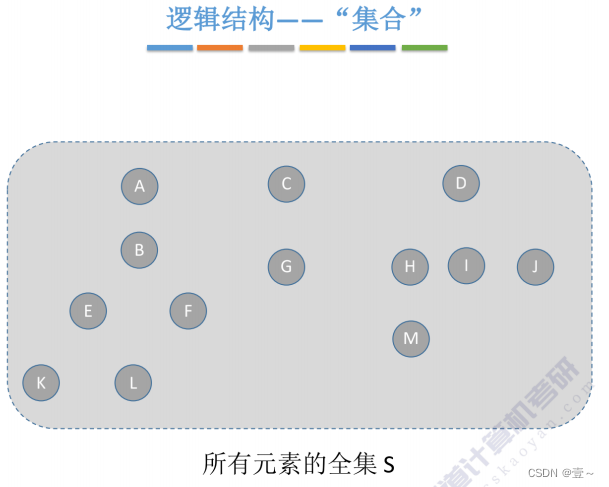
这个时候我们可以将集合之间的关系类似地看成是森林，而每个集合中的元素也可以组成一棵树。

13.1 查和并的实现

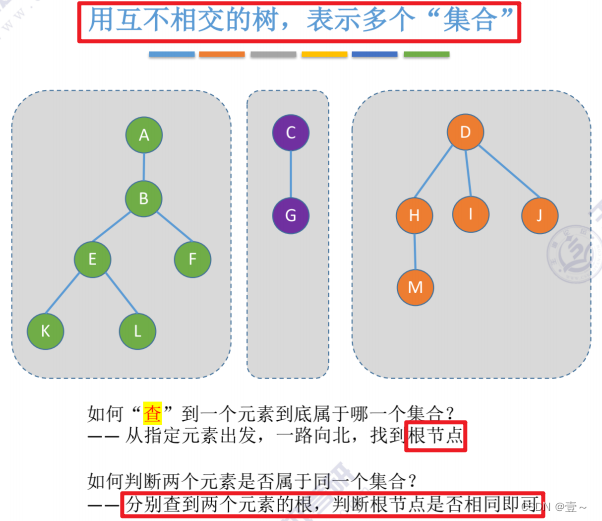
13.2 并查集的存储结构

可以用双亲表示法来存储并查集。

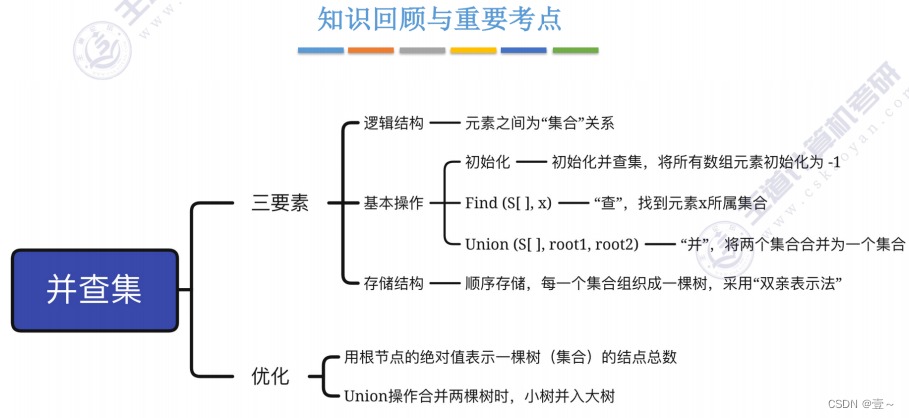
13.3 基本操作

13.4 代码实现

13.5 Union操作的优化

优化思路：在每次Union操作构建树的时候，尽量不要让树“长高”。
①用根结点的绝对值表示树的结点总数。
②Union操作，让小树合并到大树。

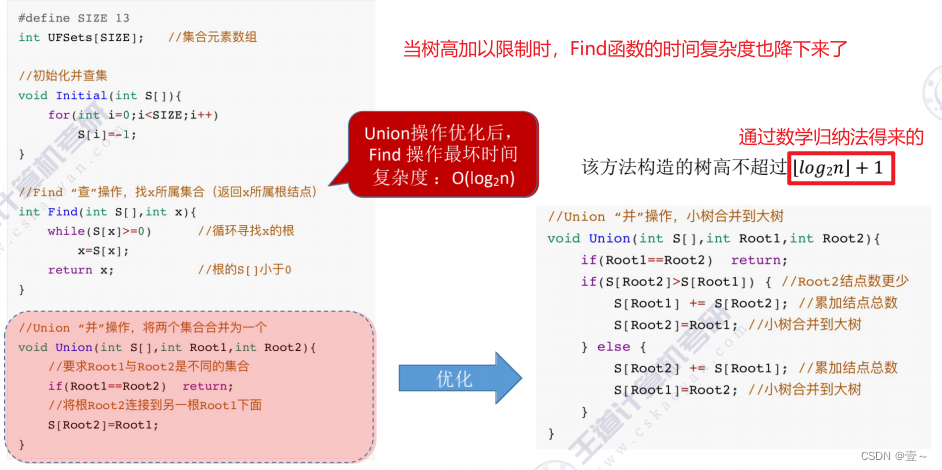
13.6 Find操作的优化（压缩路径）

每次Union时，都需要从指定元素出发找到该元素的根结点，也就是需要乘上Find函数的时间复杂度。