工业蒸汽量预测(一)
赛题理解
1、评估指标
预测结果以均方误差MSE(Mean Squared Error)为评判标准,计算公式如下:
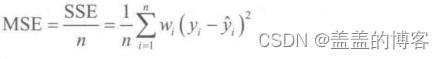
MSE是衡量“平均误差”的一种较为方便的方法。其值越小,说明预测模型描述实验数据具有越高的准确度,在sklearn中可以直接调用mean_squared_error()函数计算MSE,调用方法如下:

2、赛题模型
在机器学习中,根据问题类型的不同,常用的模型包括回归预测模型和分类预测模型。
回归问题:
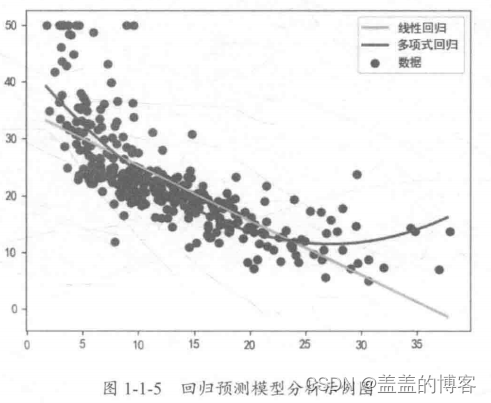
分类问题:

3、解题思路
在本赛题中,需要根据提供的V0~V37共38个特征变量来预测蒸汽量的数值,其预测值为连续型数值变量,故此问题为回归预测求解。
理论知识
1、变量识别
分清输入变量与输出变量,看清数据类型是字符型还是数值型,弄清楚连续型变量与类别型变量。
2、变量分析
2.1单变量分析
对于连续型变量,需要统计数据的中心分布趋势和变量的分布,如对下表中的数据进行分析:
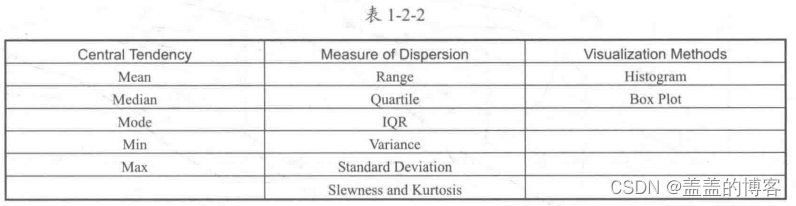
对于类别型变量,一般使用频次或占比表示每一个类别的分布情况,对应的衡量指标分别是类别变量的频次(次数)和频率(占比),可以用柱形图来表示可视化分布情况。
2.2双变量分析
使用双变量分析可以发现变量之间的关系。根据变量类型的不同,可以分为连续型与连续型、类别型与类别型、类别型与连续型三种双变量分析组合。
(1)连续型与连续型。绘制散点图和计算相关性是分析连续型与连续型双变量的常用方法。

一般来说, 在取绝对值后,0 ~ 0.09 为没有相关性,0.1 ~ 0.3 为弱相关,0.3 ~ 0.5 为中等相关,0.5 ~1.0为强相关。
(2)类别型与类别型。一般采用双向表、堆叠柱状图和卡方检验进行分析。
●双向表:这种方法是通过建立频次(次数)和频率(占比)的双向表来分析变量之间的关系,其中行和列分别表示一个变量,如表1-2-3 所示。
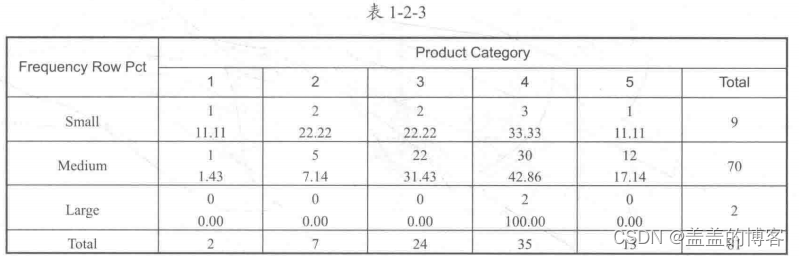
●堆叠柱状图:更直观

●卡方检验:主要用于两个和两个以上样本率(构成比)及两个二值型离散变量的关联性分析,即比较理论频次与实际频次的吻合程度或拟合优度。

(3)类别型与连续型。在分析类别型和连续型双变量时,可以绘制小提琴图(ViolinPlot),这样可以分析类别变量在不同类别时,另一个连续变量的分布情况。
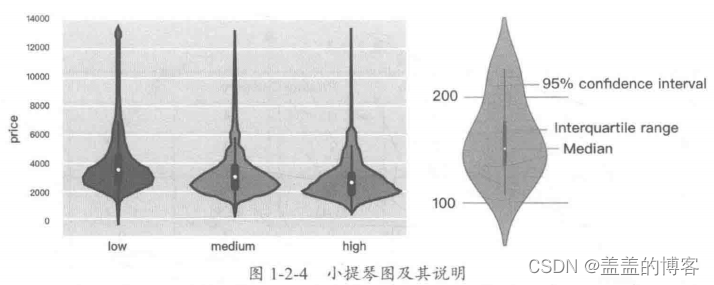
小提琴图结合了箱形图和密度图的相关特征信息,可以直观、清晰地显示数据的分布,常用于展示多组数据的分布及相关的概率密度。
说明:建议使用Seaborn包中的violinplot()函数。
3、缺失值处理
3.1删除: 分为成列删除和成对删除。

3.2平均值、众数、中值填充: 具体操作为一般填充和相似样本填充。
一般填充是用该变量下所有非缺失值的平均值或中值来补全缺失值。
相似样本填充是利用具有相似特征的样本的值或者近似值进行填充。
3.3预测模型填充: 通过建立预测模型来填补缺失值。在这种情况下,会把数据集分为两份:一份是没有缺失值的,用作训练集;另一份是有缺失值的,用作测试集。这样,缺失的变量就是预测目标,此时可以使用回归、分类等方法来完成填充。
当然,这种方法也有不足之处。首先,预测出来的值往往更加“规范”;其次,如果变量之间不存在关系,则得到的缺失值会不准确。
4、异常值处理
异常值对模型和预测分析的影响主要有增加错误方差,降低模型的拟合能力;异常值的非随机分布会降低正态性;与真实值可能存在偏差:影响回归、方差分析等统计模型的基本假设。
4.1 异常值检测
一般可以采用可视化方法进行异常值的检测,常用工县包括箱线图、直方图、散点图等。
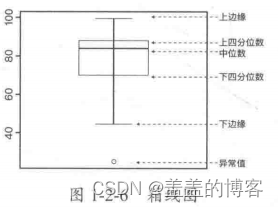
利用箱线图检测异常值的原则如下:
不在-1.5 * IQR和1.5 * IQR之间的样本点认为是异常值;
使用封顶方法可以认为在第5和第95百分位数范围之外的任何值都是异常值;
距离平均值为三倍标准差或更大的数据点可以被认为是异常值。
4.2 异常值处理
对异常值一般采用删除、转换、填充、区别对待等方法进行处理。
●删除: 如果是由输入误差、数据处理误差引起的异常值,或者异常值很小,则可以直接删除。
●转换: 数据转换可以消除异常值,如对数据取对数会减轻由极值引起的变化。
例如,图1-2-10所示即为取对数前后的数据分布直方图,可以看到转换后的数据分布更加均匀,没有明显的异常值。
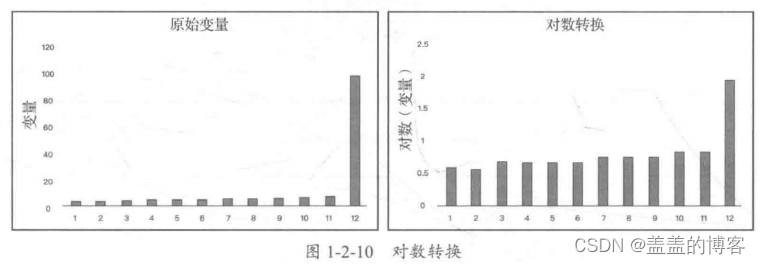
●填充:像处理缺失值一样,使用平均值、中值或其他的一些填补方法。在填补之前,需要分析异常值是自然形成的,还是人为造成的。如果是人为造成的,则可以进行填充处理,如使用预测模型填充。
● 区别对待:如果存在大量的异常值,则应该在统计模型中区别对待。其中一个方法是将数据分为两个不同的组,异常值归为一组,非异常值归为一组,且两组分别建立模型,然后最终将两组的输出合并。
5、变量转换
在使用直方图、核密度估计等工县对特征分布进行分析的过程中,我们可能会发现一些变量的取值分布不平均,这将会极大影响估计。为此,我们需要对变量的取值区间等进行转换,使其分布落在合理的区间内。

下面具体介绍几种常用的转换方法:
(1)对数变换: 对变量取对数,可以更改变量的分布形状。其通常应用于向右倾斜的分布,缺点是不能用于含有零或负值的变量。
(2)取平方根或立方根: 变量的平方根和立方根对其分布有波形的影响。取平方根可用于包括零的正值,取立方根可用于取值中有负值(包括零)的情况。
(3)变量分组: 对变量进行分类,如可以基于原始值、百分比或频率等对变量分类。例如,我们可以将收入分为高、中、低三类。其可以应用于连续型数据,超高维逻辑回归就是采取这种方式产生one-hot变量特征的。
6、新变量生成
变量生成是基于现有变量生成新变量的过程。生成的新变量可能与目标变量有更好的相关性,有助于进行数据分析。
如输入变量Date (dd-mm-yy, 日期),可以拆分生成新变量,日、月、年、周、工作日,也可能会发现与目标变量相关性更强的新变量。
有两种生成新变量的方法:
(1)创建派生变量: 指使用一组函数或不同方法从现有变量创建新变量。例如,在某个数据集中需要预测缺失的年龄值,为了预测缺失项的价值,我们可以提取名称中的称呼(Master,Mr, Miss, Mrs) 作为新变量。
(2)创建哑变量: 哑变量方法可将类别型变量转换为数值型变量。如Var. _Male (男性)和Var. Female (女性)这两个数值型变量,等效于类别型变量中的Gender (性别)。
数据探索
1、导包
2、读取数据
train_data_file = "./zhengqi_train.txt"
test_data_file = "./zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
3、查看数据
查看训练集的统计信息:
train_data.describe()
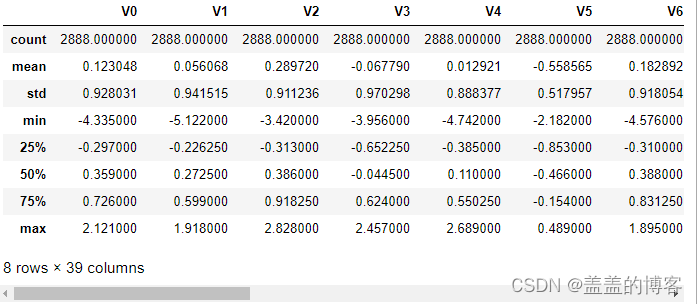
上面结果显示了数据的统计信息,如样本数、数据的均值(mean)、 标准差(std)、 最小值、最大值等。
4、可视化数据分布
4.1箱型图
fig = plt.figure(figsize=(4,6)) #指定绘图对象的宽度和高度
#sns.boxplot(train_data['V0'],orient="v",width=0.5) 图像是横着的
sns.boxplot(data=train_data['V0'],width=0.5)
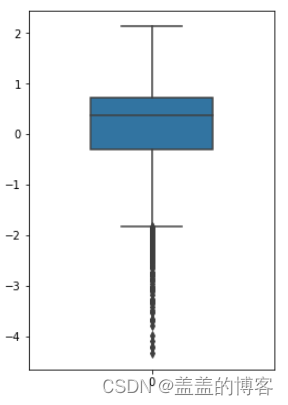
从图中可以看出有偏离值,许多数据点位于下四分位点以下。
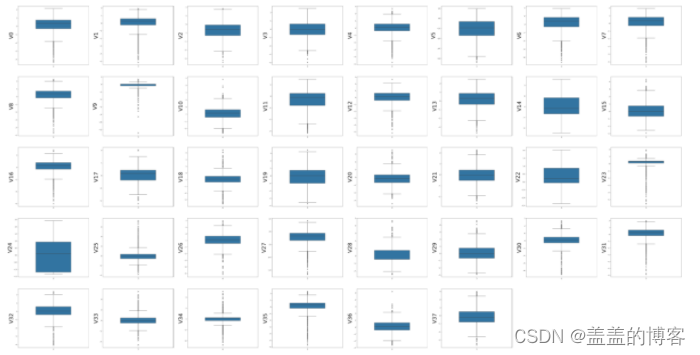
然后绘制训练集中变量V0~V37的箱形图:
column = train_data.columns.tolist()[:39] #列表头
fig = plt.figure(figsize=(80,60),dpi=75) #指定绘图对象的宽度和高度
for i in range(38):
plt.subplot(7,8,i+1) #7行8列子图
sns.boxplot(data=train_data[column[i]],width=0.5) #箱式图
plt.ylabel(column[i],fontsize=36)
plt.show()
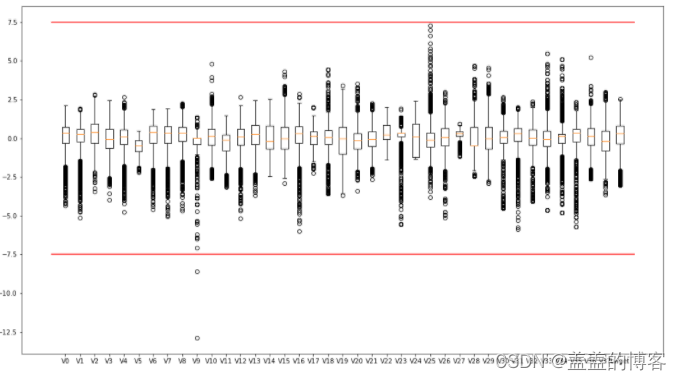
plt.figure(figsize=(18,10))
plt.boxplot(x=train_data.values,labels=train_data.columns)
plt.hlines([-7.5,7.5],0,40,colors='r')
plt.show()
#另一种方法,用plt自带的方法画箱型图
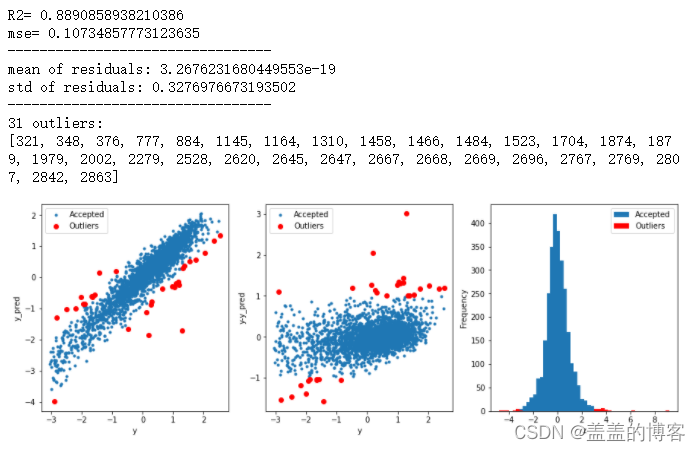
4.2获取异常数据并画图
此方法是采用模型预测的形式找出异常值。
#function to detect outliers based on the predictions of a model
def find_outliers(model,X,y,sigma=3):
#predict y values using model
try:
y_pred = pd.Series(model.predict(X),index=y.index)
#if predicting fails,try fitting the model first
except:
model.fit(X,y)
y_pred = pd.Series(model.predict(X),index=y.index)
#calculate residuals between the model prediction and true y values
resid = y - y_pred
mean_resid = resid.mean()
std_resid = resid.std()
#calculate z statistic, define outliers to be where |z| > sigma
z = (resid - mean_resid)/std_resid
outliers = z[abs(z)>sigma].index
#print and plot the results
print('R2=',model.score(X,y))
print('mse=',mean_squared_error(y,y_pred))
print('---------------------------------')
print('mean of residuals:',mean_resid)
print('std of residuals:',std_resid)
print('---------------------------------')
print(len(outliers),'outliers:')
print(outliers.tolist())
plt.figure(figsize=(15,5))
ax_131 = plt.subplot(1,3,1)
plt.plot(y,y_pred,'.')
plt.plot(y.loc[outliers],y_pred.loc[outliers],'ro')
plt.legend(['Accepted','Outliers'])
plt.xlabel('y')
plt.ylabel('y_pred');
ax_132=plt.subplot(1,3,2)
plt.plot(y,y-y_pred,'.')
plt.plot(y.loc[outliers],y.loc[outliers]-y_pred.loc[outliers],'ro')
plt.legend(['Accepted','Outliers'])
plt.xlabel('y')
plt.ylabel('y-y_pred');
ax_133=plt.subplot(1,3,3)
z.plot.hist(bins=50,ax=ax_133)
z.loc[outliers].plot.hist(color='r',bins=50,ax=ax_133)
plt.legend(['Accepted','Outliers'])
plt.xlabel('z')
plt.savefig('outliers.png')
return outliers
#通过岭回归模型找出异常值,并绘制其分布
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
X_train=train_data.iloc[:,0:-1]
y_train=train_data.iloc[:,-1]
outliers = find_outliers(Ridge(),X_train, y_train)
4.3直方图和QQ图
Q-Q图是指数据的分位数和正态分布的分位数对比参照的图,如果数据符合正态分布,则所有的点都会落在直线上。
首先,通过绘制特征变量V0的直方图查看其在训练集中的统计分布,并绘制Q-Q图查看V0的分布是否近似于正态分布。
plt.figure(figsize=(10,5))
ax=plt.subplot(1,2,1)
sns.distplot(train_data['V0'],fit=stats.norm)
ax=plt.subplot(1,2,2)
res=stats.probplot(train_data['V0'],plot=plt)
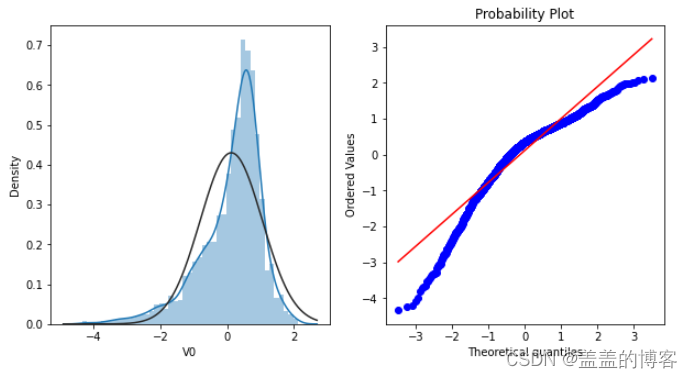
可以看到,训练集中特征变量V0的分布不是正态分布。
然后,绘制训练集中所有变量的直方图和Q-Q图。
train_cols = 6
train_rows = len(train_data.columns)
plt.figure(figsize=(4*train_cols,4*train_rows))
i=0
for col in train_data.columns:
i+=1
ax=plt.subplot(train_rows,train_cols,i)
sns.distplot(train_data[col],fit=stats.norm)
i+=1
ax=plt.subplot(train_rows,train_cols,i)
res=stats.probplot(train_data[col],plot=plt)
plt.tight_layout()
plt.show()
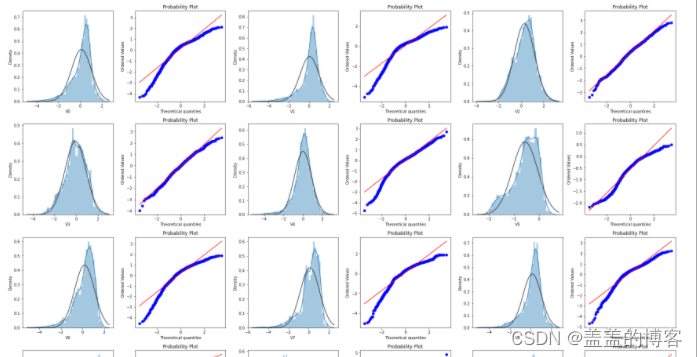
从数据分布图可以发现,很多特征变量(如V1,V9,V24,V28等)的数据分布不是正态的,
数据并不跟随对角线分布,后续可以使用数据变换对其进行处理。
4.4KDE分布图
KDE ( Kernel Density Estimation,核密度估计)可以理解为是对直方图的加窗平滑。通过绘制KDE分布图,可以查看并对比训练集和测试集中特征变量的分布情况,发现两个数据集中分布不一致的特征变量。
首先对比同一特征变量V0在训练集和测试集中的分布情况,并查看数据分布是否–致。
plt.figure(figsize=(8,4),dpi=150)
ax = sns.kdeplot(train_data['V0'],color="Red", shade=True)
ax = sns.kdeplot(test_data['V0'],color="Blue", shade=True)
ax.set_xlabel('V0')
ax.set_ylabel("Frequency")
ax = ax.legend(["train","test"])
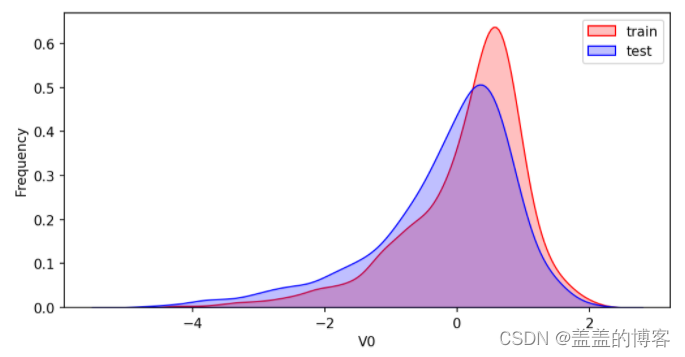
可以看到,V0在两个数据集中的分布基本一致。
然后,对比所有变量在训练集和测试集中的KDE分布。
dist_cols = 6
dist_rows = len(test_data.columns)
plt.figure(figsize=(4 * dist_cols, 4 * dist_rows))
i = 1
for col in test_data.columns:
ax = plt.subplot(dist_rows,dist_cols,i)
ax = sns.kdeplot(train_data[col],color="Red",shade=True)
ax = sns.kdeplot(test_data[col],color="Blue",shade=True)
ax.set_xlabel(col)
ax.set_ylabel("Frequency")
ax = ax.legend(["train","test"])
i += 1
plt.show()
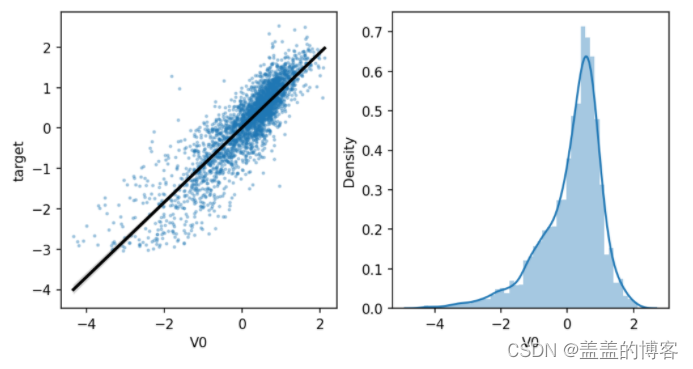
4.5线性回归关系图
fcols = 2
frows = 1
plt.figure(figsize=(8,4),dpi=150)
ax=plt.subplot(1,2,1)
sns.regplot(x='V0',y='target',data=train_data,ax = ax,scatter_kws={'marker':'.','s':3,'alpha':0.3},line_kws={'color':'k'});
plt.xlabel('V0')
plt.ylabel('target')
ax=plt.subplot(1,2,2)
sns.distplot(train_data['V0'].dropna())
plt.xlabel('V0')
plt.show()
5、查看特征变量的相关性
5.1计算相关性系数
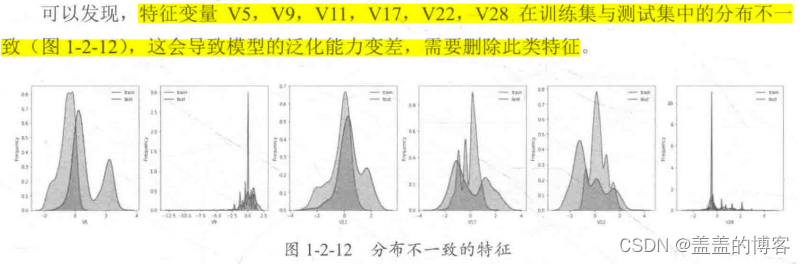
在删除训练集和测试集中分布不一致的特征变量,如V5,V9, V11, V17, V22,V28之后,计算剩余特征变量及target变量的相关性系数。
pd.set_option('display.max_columns',10)
pd.set_option('display.max_rows',10)
data_train1 = train_data.drop(['V5','V9','V11','V17','V22','V28'],axis=1)
train_corr = data_train1.corr()
train_corr
5.2画出相关性热力图
ax=plt.subplots(figsize=(20,16)) #调整画布大小
ax = sns.heatmap(train_corr, vmax=.8, square=True, annot=True) #画热力图
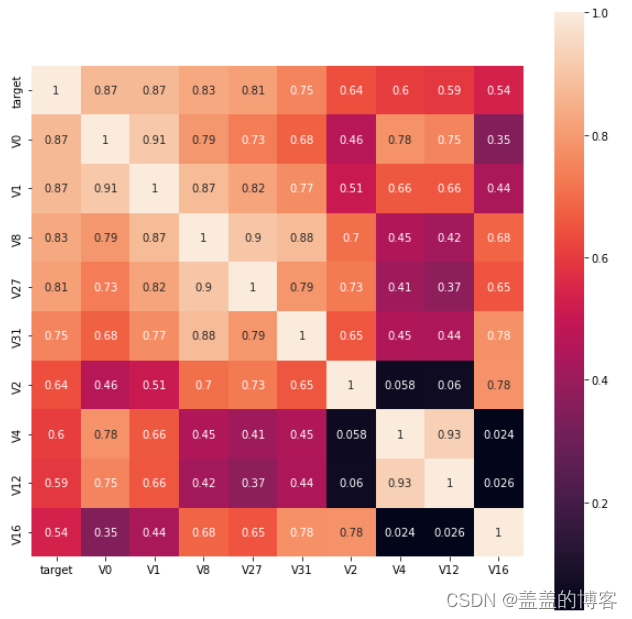
5.3筛选特征变量
根据相关系数筛选K个最相关的特征变量:
k = 10
cols = train_corr.nlargest(k,'target')['target'].index
cm = np.corrcoef(train_data[cols].values.T)
hm = plt.subplots(figsize=(10,10)) #调整画布大小
hm = sns.heatmap(train_data[cols].corr(),annot=True, square = True)
plt.show()
找出相关系数>0.5的特征变量:
threshold = 0.5
corrmat = train_data.corr()
top_corr_features = corrmat.index[abs(corrmat["target"]) > threshold]
plt.figure(figsize=(10,10))
g = sns.heatmap(train_data[top_corr_features].corr(),annot = True,cmap="RdYlGn")
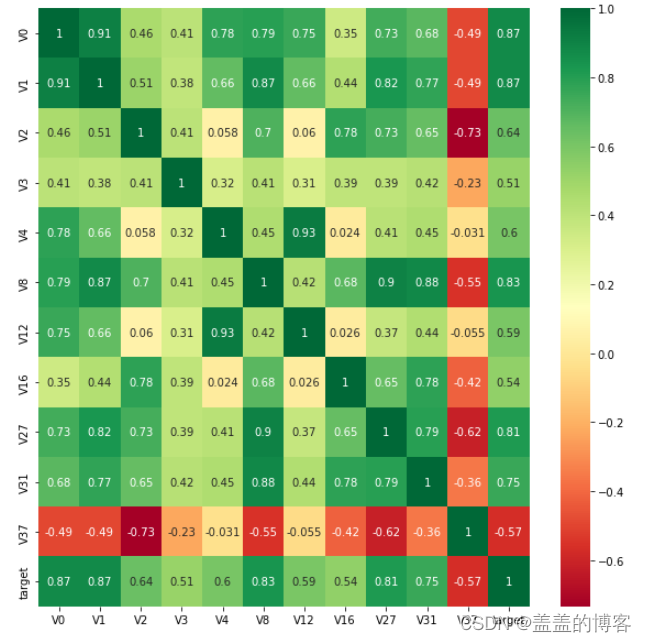
可以将一些不重要的特征删除,方便快速分析重要特征。
说明:相关性选择主要用于判别线性相关,对于target变量如果存在更复杂的函数形式的影响,则建议使用树模型的特征重要性去选择。
5.4Box-Cox变换
由于线性回归是基王正态分布的,因此在进行统计分析时,需要将数据转换使其符合正态分布。
Box-Cox变换是统计建模中常用的一种数据转换方法。在连续的响应变量不满足正态分布时,可以使用Box-Cox变换,这一变换可以使线性回归模型在满足线性、正态性、独立性及方差齐性的同时,又不丢失信息。在对数据做Box-Cox变换之后,可以在一定程度上减小不可观测的误差和预测变量的相关性,这有利于线性模型的拟合及分析出特征的相关性。
在做Box-Cox变换之前,需要对数据做归一化预处理。在归一化时,对数据进行合并操作可以使训练数据和测试数据一致。这种方式可以在线下分析建模中使用,而线上部署只需采用训练数据的归一化即可。
#pandas归一化
cols_numeric = list(X_train.columns)
def scale_minmax(col):
return(col-col.min())/(col.max()-col.min())
X_train_s = X_train[cols_numeric].apply(scale_minmax,axis = 0)
X_train_s.describe()
#sklearn归一化
from sklearn import preprocessing
features_columns = list(X_train.columns)
min_max_scaler = preprocessing.MinMaxScaler()
min_max_scaler = min_max_scaler.fit(X_train[features_columns])
X_train_scaler = pd.DataFrame(min_max_scaler.transform(X_train[features_columns]))
X_test_scaler = pd.DataFrame(min_max_scaler.transform(X_test[features_columns]))
X_test_data_scaler = pd.DataFrame(min_max_scaler.transform(test_data[features_columns]))
对特征变量做Box-Cox变换后,计算分位数并画图展示(基于正态分布),显示特征变量与target变量的线性关系。示例代码如下:
fcols = 6
frows = len(cols_numeric_left)
plt.figure(figsize=(4*fcols,4*frows))
i = 0
for var in cols_numeric_left:
dat = train_data_process[[var,'target']].dropna()
i += 1
plt.subplot(frows,fcols,i)
sns.distplot(dat[var], fit = stats.norm)
plt.title(str(var) + 'Original')
plt.xlabel('')
i += 1
plt.subplot(frows,fcols,i)
_ = stats.probplot(dat[var],plot = plt)
plt.title('skew' + '{:.4f}'.format(stats.skew(dat[var])))
plt.xlabel('')
plt.ylabel('')
i += 1
plt.subplot(frows,fcols,i)
plt.plot(dat[var],dat['target'],'.',alpha = 0.5)
plt.title('corr=' + '{:.2f}'.format(np.corrcoef(dat[var],dat['target'])[0][1]))
i += 1
plt.subplot(frows,fcols,i)
trans_var,lambda_var = stats.boxcox(dat[var].dropna() + 1)
trans_var = scale_minmax(trans_var)
sns.distplot(trans_var,fit=stats.norm)
plt.title(str(var) + 'Tramsformed')
plt.xlabel('')
i += 1
plt.subplot(frows,fcols,i)
_ = stats.probplot(trans_var,plot = plt)
plt.title('skew=' + '{:.4f}'.format(stats.skew(trans_var)))
plt.xlabel('')
plt.ylabel('')
i += 1
plt.subplot(frows,fcols,i)
plt.plot(trans_var,dat['target'],'.',alpha = 0.5)
plt.title('corr=' + '{:.2f}'.format(np.corrcoef(trans_var,dat['target'])[0][1]))
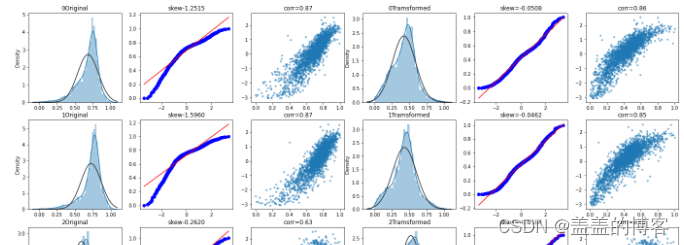
可以发现,经过变换后,变量分布更接近正态分布,而且从图中可以更加直观地看出特
征变量与target变量的线性相关性。






















 1082
1082











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








