状态压缩DP例题

荼白777

已于 2022-03-28 21:13:33 修改

阅读量323

点赞数

分类专栏： DP 文章标签：动态规划算法

于 2021-11-04 10:47:45 首次发布

本文链接：https://blog.csdn.net/weixin_45724872/article/details/121135378

版权

DP 专栏收录该内容

19 篇文章 0 订阅

订阅专栏

引入

状压DP一般分为两种，一种是基于连通性(棋盘状)的，另一种是基于集合的；

例题（棋盘形）

小国王

题面

小国王

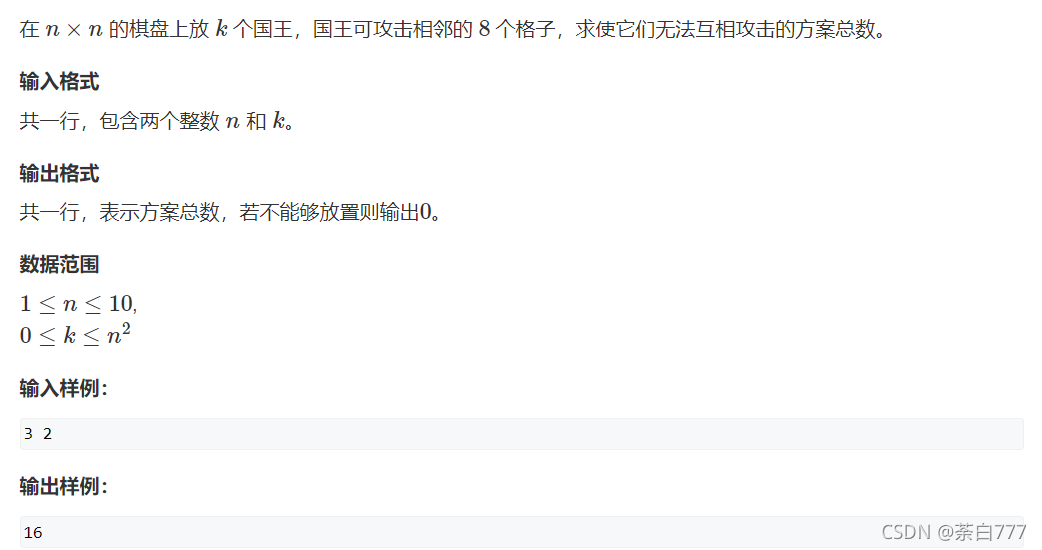
在这里插入图片描述

思路

不难发现，假设现在是第 $i$ 行，它的国王怎么放

只取决于 $i - 1$ 行；

因此我们可以考虑定义状态 $f (i, s)$ 表示前 $i$ 行，第 $i$ 行的状态是 $s$ 的所有方案；

但是发现又有次数这个限制

因此我们定义状态

$f (i, j, s)$ 表示所有只摆在前i行，已经摆了 $j$ 个国王，第 $i$ 行摆放的状态是 $s$ 的所有方案；

现在考虑状态转移，因为只与前一行有关；

我们假设第 $i$ 行的状态是 $a$ ，第 $i - 1$ 行的状态是 $b$ ；

首先要满足下面的条件；

在这里插入图片描述
用代码来表示的话，如下

那么在满足上面条件合法的情况下，我们有如下方程；

$f (i, j, a) \leftarrow f (i - 1, j - c o u n t (a), b)$

其中 $c o u n t (a)$ 是状态 $a$ 中 $1$ 的数量；

接着考虑时间复杂度

DP的时间复杂度一般为：

$状态数量 * 状态转移的计算量$

那么最坏情况下，时间为 $n * k * 状态 * 合法转移方案$ ，差不多 $10^9$ ；

因为合法转移方案不多，时间近似为 $10^6$

Code

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e1 + 10,M = 1<<12,K = 1e2 + 10;

int n,k,nums[M];

ll f[N][K][M];

vector<int> valid;//合法状态
vector<int> head[M];//合法转移

bool check(int x){
    //不能有相邻两个1
    return !(x & x >> 1);
}
int count(int x){
    int ret = 0;
    while(x){
        if(x&1) ++ret;
        x >>= 1;
    }
    return ret;
}
void solve(){
    cin >> n >> k;
    //预处理所有合法状态
    for(int s=0;s<(1<<n);++s){
        if(check(s)){
            valid.push_back(s);
            nums[s] = count(s);
        }
    }

    //预处理所有合法状态的合法转移
    for(auto a : valid)
        for(auto b : valid)
            if(!(a&b) && check(a|b))
                head[a].push_back(b);
    
    f[0][0][0] = 1;
    for(int i=1;i<=n;++i)
        for(int j=0;j<=k;++j)
            for(auto a : valid)
                for(auto b : head[a])
                    if(j - nums[a] - nums[b] >= 0)
                        f[i][j][a] += f[i-1][j-nums[a]][b];

    ll ans = 0;
    for(int s=0;s<1<<n;++s) ans += f[n][k][s];
    cout << ans << '\n';
}

int main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

玉米田

题面

玉米田

在这里插入图片描述

思路

和上题类似，只不过上题是禁止八连通，这题是禁止四连通；

题目说的贫瘠土地我们可以先拿一个数组存下来，等待状态转移的时候再判断；

Code

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>

using namespace std;

typedef long long ll;

const int MOD = 1e8;

const int N = 1e1 + 10,M = 1<<13;

int n,m;

vector<int> state; //合法状态
vector<int> head[M]; //合法状态的转移

int a[N];

ll f[N][M];

bool check(int x){
    return !(x & x << 1);
}

void solve(){
    cin >> n >> m;
    for(int i=1;i<=n;++i)
        for(int j=0;j<m;++j){
            int u;
            cin >> u;
            //1表示不能种，方便我们与运算
            a[i] |= (!u) << j;
        }
    for(int s=0;s<1<<m;++s){
        if(check(s)) state.push_back(s);
    }
    for(auto a : state)
        for(auto b : state)
            if(!(a&b))
                head[a].push_back(b);
    f[0][0] = 1;
    for(int i=1;i<=n;++i){
        for(auto s : state){
            //种玉米的土地是贫瘠的
            if(s & a[i]) continue;
            for(auto b : head[s]){
                f[i][s] += f[i-1][b];
                f[i][s] %= MOD;
            }
        }
    }
    ll ans = 0;
    //非法状态为0 不需要考虑
    for(auto s : state) ans = (ans%MOD+f[n][s]%MOD)%MOD;
    cout << ans << '\n';
}

int main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

炮兵阵地

题面

炮兵阵地

在这里插入图片描述

思路

不难发现，这题就是上一题的扩展；

在上一题中，棋子的占领范围是 $1$

而这题棋子的占领范围是是 $2$

如果我们只压缩当前层一层状态后进行转移，是不能保证该次转移是合法的；

因此我们可以参考上一题，攻击范围是 $1$ ，压缩了一层状态；

那我们就压缩两层状态进行转移，其他都一样；

设 $f (i, j, k)$ 表示前 $i$ 层，第 $i$ 层状态是 $j$ ，第 $i - 1$ 层状态是 $k$ 的所有方案中的最大值；

假设第 $i$ 层状态是 $s$ ， $i - 1$ 层状态是 $s_1$ ， $i - 2$ 层状态是 $s_2$

很容易得 $f(i,s,s_1)←f(i-1,s_1,s_2) + nums(s)$

$n u m s (s)$ 是状态 $s$ 中 $1$ 的个数；

小技巧1

此外，我们发现，每一次的状态 $i$ ，都是由 $i - 1$ 转移；

因此我们可以考虑滚动数组；

滚动数组的话，有一种简便的写法；

就是开 $2$ 维，先照常写，然后需要滚动的地方加 $\&1$ 即可；

自然就会 $0, 1$ 切换了;

就不用费心思去写一维度的滚动数组；

小技巧2

在其他都不变的情况下，我们最后枚举 $d p$ ，可以枚举到 $n + 2$ ；

这样我们输出答案的时候，只需要输出 $f (n + 2, 0, 0)$ 即可；

像上两题，棋子攻击范围是 $1$ 的，我们只需要枚举到 $n + 1$ ；

输出答案的时候，输出 $f (n + 1, 0)$ 即可;

Code

只加了优化一

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e1 + 10,M = 1<<10;

int n,m;
//f(i,j,k) 前i层，第i层状态是j，第i−1层状态是k的所有方案中的最大值
int f[2][M][M];

int nums[M];

vector<int> state;
vector<int> head[M];

int g[N];

bool check(int state){
    //相邻两格之间不能有'1'
    return !((state & state << 1) || (state & state << 2));
}

int count(int x){
    int ret = 0;
    while(x){
        if(x&1) ++ret;
        x>>=1;
    }
    return ret;
}

void solve(){
    cin >> n >> m;
    char ch;
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j){
            cin >> ch;
            if(ch == 'H'){
                //不能放的赋1
                g[i] |= 1<<(j-1);
            }
        }
    //枚举合法状态
    for(int s=0;s<1<<m;++s){
        if(check(s)){
            state.push_back(s);
            nums[s] = count(s);
        }
    }
    //枚举合法转移
    for(auto a : state)
        for(auto b : state)
            if(!(a&b)) head[a].push_back(b);
    //DP
    for(int i=1;i<=n;++i){
        for(auto s : state){
            if(g[i] & s) continue;
            for(auto s_1 : head[s]){
                for(auto s_2 : head[s_1]){
                    //我们现在的枚举顺序
                    //只能保证(s,s-1),(s-1,s-2)是互不冲突的
                    //因此还要判断(s,s-2)是否冲突
                    if(!(s&s_2)){
                        f[i&1][s][s_1] = max(f[i&1][s][s_1],f[(i-1)&1][s_1][s_2] + nums[s]);
                    }
                }
            }
        }
    }
    //计算最终结果
    int ans = 0;
    for(auto s : state){
        for(auto s_1 : head[s]){
            ans = max(ans,f[n&1][s][s_1]);
        }
    }
    cout << ans << '\n';
}

int main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

加了优化一和优化二的

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e1 + 10,M = 1<<10;

int n,m;
//f(i,j,k) 前i层，第i层状态是j，第i−1层状态是k的所有方案中的最大值
int f[2][M][M];

int nums[M];

vector<int> state;
vector<int> head[M];

int g[N];

bool check(int state){
    //相邻两格之间不能有'1'
    return !((state & state << 1) || (state & state << 2));
}

int count(int x){
    int ret = 0;
    while(x){
        if(x&1) ++ret;
        x>>=1;
    }
    return ret;
}

void solve(){
    cin >> n >> m;
    char ch;
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j){
            cin >> ch;
            if(ch == 'H'){
                //不能放的赋1
                g[i] |= 1<<(j-1);
            }
        }
    //枚举合法状态
    for(int s=0;s<1<<m;++s){
        if(check(s)){
            state.push_back(s);
            nums[s] = count(s);
        }
    }
    //枚举合法转移
    for(auto a : state)
        for(auto b : state)
            if(!(a&b)) head[a].push_back(b);
    //DP
    for(int i=1;i<=n+2;++i){
        for(auto s : state){
            if(g[i] & s) continue;
            for(auto s_1 : head[s]){
                for(auto s_2 : head[s_1]){
                    //我们现在的枚举顺序
                    //只能保证(s,s-1),(s-1,s-2)是互不冲突的
                    //因此还要判断(s,s-2)是否冲突
                    if(!(s&s_2)){
                        f[i&1][s][s_1] = max(f[i&1][s][s_1],f[(i-1)&1][s_1][s_2] + nums[s]);
                    }
                }
            }
        }
    }

    cout << f[n+2 & 1][0][0] << '\n';
}

int main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

蒙德里安的梦想

题面

蒙德里安的梦想

在这里插入图片描述

思路

这题虽然不像上面那几题给我们画出明显的棋盘，但是我们自行画出 $n * m$ 的矩形后分割，发现还是棋盘形；

核心思路是，先放横着的方块，再放竖着的方块；

可以发现，如果横着方块已经放好了，那么竖着的方块只能插进其中，而无论怎么插，都是一种方案；

因此总方案数 $=$ 只放横着的方块的合法方案数

合法的方案，那么有以下两点

摆放横着的方块必然不能重合
摆完后剩下的空间可以摆竖着的方块

对于第一点，我们直接与就可以解决；

对于第二点，我们需要判断摆放完后，剩下的位置是不是奇数

Code

#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e1 + 10 , M = 1 << 11;

vector<int> head[M];

int n,m;

bool check(int state){
    int cnt = 0;
    for(int j=0;j<n;++j){ //看看每一位的状态
        if(state >> j & 1){
            if(cnt & 1){
               //说明有长度为奇数的缝隙
               return false;
            }
        }
        else ++cnt;
    }
    //如果最后存在长度为奇数的缝隙
    return cnt&1?false:true;
}
//f(i,s)表示前i-1列已经摆好，第i-1列延申到第i列的状态为s
ll f[N][M];

bool st[M];

void solve(){
    memset(st,0,sizeof st);
    memset(f,0,sizeof f);
    for(int s=0;s<1<<n;++s){
        head[s].clear();
        //这里不能直接丢到state认为是合法状态
        //假设现在i-1 -> i 出现的状态是奇数
        //但是加入i-2 -> i-1后 可能就变成偶数了
        st[s] = check(s);
    }
    //因为只和i-2,i-1,i有关系，而且主体是i-1，因此两重枚举即可
    for(int a=0;a<1<<n;++a)
        for(int b=0;b<1<<n;++b)
            //st[a|b]即同时考虑了i-2 -> i-1 与 i-1 -> i 后，第i-1列是否存在奇数个0
            if((a&b) == 0 && st[a|b]) 
                head[a].push_back(b);
    
    f[0][0] = 1;
    for(int i=1;i<=m;++i){
        for(int s=0;s<1<<n;++s){
            for(auto s_1 : head[s]){
                f[i][s] += f[i-1][s_1];
            }
        }
    }
    //f(1,?)表示第0列延申到第1列
    //因此f(m,?)表示第m列延申到第m+1列 因此状态为0
    cout << f[m][0] << '\n';
}

int main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    while(cin >> n >> m,(n||m)){
        solve();
    }
    return 0;
}

例题(集合形)

最短Hamilton路径

题面

最短Hamilton路径

在这里插入图片描述

思路

设 $f (i, s)$ 表示当前在点 $i$ ，状态为 $s$ 的所有方案中的最小值

状态转移：假设当前要从 $j$ 转移到 $i$ ；

那么根据 $H a m i l t o n$ 路径的定义，走到 $j$ 的时候，我们不能经过 $i$ ；

因此有下述转移方程；

f[i][state] = min{f[j][state ^ (1 << j)] + a[k][j]}

Code

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 2e1 + 10 , M = 1 << 21;

//f(i,s)表示当前在点i，状态为s的所有方案中的最小值
int f[N][M];

int a[N][N];

void solve(){
    int n;
    cin >> n;
    for(int i=0;i<n;++i)
        for(int j=0;j<n;++j)
            cin >> a[i][j];
    memset(f,0x3f,sizeof f);
    f[0][1] = 0;
    for(int s=0;s<1<<n;++s)
        //必须包含0
        if(s & 1)
            for(int i=0;i<n;++i)//当前在i
                if(s >> i & 1)
                    for(int j=0;j<n;++j){ //从j转移到i
                        if(j == i) continue;
                        //不能包含i 必须包含j
                        if( (s^(1<<i) >> j & 1))
                            f[i][s] = min(f[i][s],f[j][s^(1<<i)] + a[j][i]);
                    } 
    cout << f[n-1][(1<<n)-1] << '\n';
}

int main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

吃奶酪

题面

吃奶酪
在这里插入图片描述

思路

和上题是类似的；

设 $f (i, s)$ 表示当前在点 $i$ ，状态为 $s$ 的所有方案中的最小值

因为我们状态压缩只能压缩某个奶酪取或没取；

因此我们可以认为从各个奶酪出发，来跑这个状压DP；

最后再计算从 $(0, 0)$ 点转移过去，并取一个最小值即可

Code

#include <iostream>
#include <cstdio>
#include <cmath>
#include <utility>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 20,M = 1 << 16;

typedef pair<double,double> pdd;

pdd idx[N];

double f[N][M];

double dis[N][N];

int n;

double get_dis(int i,int j){
    double d = (idx[i].first - idx[j].first)*(idx[i].first - idx[j].first)
            + (idx[i].second - idx[j].second)*(idx[i].second - idx[j].second);
    return sqrt(d);
}

void solve(){
    cin >> n;
    for(int i=0;i<n;++i) 
        cin >> idx[i].first >> idx[i].second;
    for(int i=0;i<n;++i)
        for(int j=0;j<i;++j){
            dis[i][j] = dis[j][i] = get_dis(i,j);
        }
    memset(f,0x43,sizeof f);
    //假设从各个奶酪点出发
    for(int i=0;i<n;++i)
        f[i][1<<i] = 0;
    //DP
    for(int s=0;s<1<<n;++s)
        for(int i=0;i<n;++i) //当前在i
            if(s & (1<<i))
                for(int j=0;j<n;++j){ //从j转移
                    if(i == j) continue;
                    if((s ^ (1 << i)) >> j & 1)
                        f[i][s] = min(f[i][s],f[j][s^(1<<i)] + dis[j][i]);
                }
    //从(0,0) -> 某个奶酪点出发
    double ans = 1e9,tmp;
    for(int i=0;i<n;++i){
        tmp = f[i][(1<<n)-1] +
         sqrt((idx[i].first*idx[i].first) + (idx[i].second*idx[i].second));
        ans = min(tmp,ans);
    }
    printf("%.2f\n",ans);
}

int main(){
    //std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

连锁商店

题面

连锁商店

在这里插入图片描述

思路

设 $f (i, s)$ 表示当前在点 $i$ ，状态为 $s$ ；

这个状态用于表示当前已经领取了哪些公司的红包；

因为公司的数量很多，我们不可能硬枚举所有的方案；

因为红包的数额总是大于零的，因此能领红包一定比不领好(某公司只有一家店)；

但是如果某公司有多家店，那么我们需要取舍；

因此对于状态转移来说，我们需要知道从哪个点来到 $i$ 的，并且那个点的状态是什么；

所以对于 $f (i, s)$ 来说，我们需要枚举前一个状态的所有可能方案；

所以就可以得到转移方程了；

$f(i,s_i) ← f(pre,s_{pre}) + (能否领红包)$

Code

#include <iostream>
#include <map>
#include <vector>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 50;

map<ll,ll> f[N];//f(i,s) 表示当前在点i 拥有的状态是s

vector<ll> st[N];//st(i) 为点i所拥有的状态

int c[N],w[N];

ll ans[N];

int n,m,k;

vector<int> G[N];

void update(int now){
    vector<ll> res;
    //显然重复的状态是不需要的
    sort(st[now].begin(),st[now].end());
    st[now].erase(unique(st[now].begin(),st[now].end()),st[now].end());
    for(auto x : st[now]){
        bool ok = 1;
        for(auto y : st[now]){
            if(x == y) continue;
            if((x|y) == y){
                //x是y的子集
                ok = 0;
                break;
            }
        }
        if(ok) res.push_back(x);
    }
    st[now] = res;
}

void solve(){
    cin >> n >> m;
    for(int i=1;i<=n;++i){
        cin >> c[i];
    }
    for(int i=1;i<=n;++i) cin >> w[i];
    for(int i=1,u,v;i<=m;++i){
        cin >> u >> v;
        G[v].push_back(u);
    }
    f[1][1ll<<c[1]] = w[c[1]];
    st[1].push_back(1ll << c[1]);
    ans[1] = w[c[1]];
    for(int i=2;i<=n;++i){
        for(auto pre : G[i]){
            for(auto s : st[pre]){
                //在上一个状态就有公司c了
                if(s & (1ll << c[i])){
                    if(!f[i].count(s)) st[i].push_back(s);
                    f[i][s] = max(f[i][s],f[pre][s]);
                    ans[i] = max(ans[i],f[i][s]);
                }
                else{
                    ll cur = s | (1ll << c[i]);
                    if(!f[i].count(cur)) st[i].push_back(cur);
                    f[i][cur] = max(f[i][cur],f[pre][s] + w[c[i]]);
                    ans[i] = max(ans[i],f[i][cur]);
                }
            }
        }
        //如果某个状态是另一个状态的子集
        //那么这个状态是没有用的
        //比如 11001 肯定没有 11011 优秀 (因为w_i > 0)
        update(i);
    }
    for(int i=1;i<=n;++i) cout << ans[i] << '\n';
}

int main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}