OneNet: Enhancing Time Series Forecasting Models under Concept Drift by Online Ensembling

最新推荐文章于 2024-08-28 09:32:20 发布

萧宛亦

最新推荐文章于 2024-08-28 09:32:20 发布

阅读量250

点赞数

文章标签：人工智能

原文链接：https://arxiv.org/abs/2309.12659

版权

系列文章目录

OneNet：通过在线集成增强概念漂移下的时间序列预测模型 (NeurIPS 2023)

文章目录

系列文章目录
摘要
一、引言
二、前期及相关工作
三、 OneNet: Ensemble Learning for Online Time Series Forecasting
- 3.1 Learning the best expert by Online Convex （凸）Programming (OCP)
- 3.2 OneNet: utilizing the advantages of both structures
四、 Experiments
五、 Conclusion and Future Work

摘要

`
时间序列预测模型在线更新旨在通过基于流数据高效更新预测模型来解决概念漂移问题。许多算法都是为在线时间序列预测而设计的，其中一些算法利用交叉变量依赖性，而另一些则假设变量之间的独立性。鉴于每个数据假设在在线时间序列建模中都有其自身的优点和缺点，我们提出了在线集成网络（OneNet）。它动态更新和组合两个模型，一个专注于跨时间维度的依赖关系建模，另一个专注于跨变量依赖关系建模。我们的方法将基于强化学习的方法融入到传统的在线凸编程框架中，允许动态调整权重的两个模型的线性组合。 OneNet 解决了经典在线学习方法的主要缺点，即适应概念漂移的速度往往较慢。实证结果表明，与 State-Of-The-Art (SOTA) 方法相比，OneNet 将在线预测误差降低了 50% 以上。代码可在 https://github.com/yfzhang114/OneNet 获取。

一、引言

近年来，我们目睹了将深度学习应用于时间序列预测的研究工作显着增加 [Lim 和 Zohren，2021；Wen 等人，2022]。事实证明，深度模型不仅在预测任务中表现出色，而且在表示学习中也表现出色，能够提取抽象表示，并将其有效地转移到分类和异常检测等下游任务。然而，现有的研究主要集中在批量学习设置上，假设整个训练数据集事先可用，并且输入和输出变量之间的关系在整个学习过程中保持不变。这些方法在现实世界的应用中存在不足，在现实世界的应用中，概念通常不稳定，但会随着时间的推移而变化，称为概念漂移 [Tsymbal, 2004]，其中未来的数据表现出与过去观察到的模式不同的模式。在这种情况下，从头开始重新训练模型可能会非常耗时。因此，需要在线训练深度预测器，用新样本逐步更新预测模型，以捕获环境中不断变化的动态。

现实世界的设置（称为在线预测）提出了挑战，例如与离线小批量训练相比，噪声梯度较高 [Aljundi 等人，2019a]，以及连续分布变化，这可能会使从历史数据中学习的模型对当前数据不太有效预言。虽然一些研究试图通过设计高级更新结构或学习目标来解决这些问题 [Pham et al., 2023, You et al., 2021]，但它们都依赖于 TCN 主干网 [Bai et al., 2018]，没有利用更先进的网络结构，例如 Transformer [Nie et al., 2023, Zhou et al., 2022b]。我们的研究表明，当前基于变压器的模型 PatchTST [Nie et al., 2023] 在没有任何先进的在线学习适应方法的情况下，比 SOTA 在线适应模型 FSNet [Pham et al., 2023] 表现更好，特别是对于具有挑战性的 ECL 任务（表 1）。此外，我们发现变量独立性对于 PatchTST 的稳健性至关重要。具体来说，PatchTST 专注于对时间依赖性（跨时间依赖性）进行建模并独立预测每个变量。为了验证变量独立性假设的有效性，我们设计了Time-TCN，它仅在时间维度上进行卷积。 Time-TCN 优于 FSNet（一种最先进的在线预测方法），并且与常用的在可变维度上进行卷积的 TCN 结构相比取得了显着的收益。

表 1：在线集成的一个激励示例，其中报告的指标是 MSE，预测范围长度设置为 48。单元格根据 MSE 值进行着色，从低（红色）到中（白色）再到高（蓝色的）。标题为“交叉变量”的列是指专注于建模交叉变量依赖性的方法，标题为“跨时间”的列是指仅利用时间依赖性并假设协变量之间独立的方法。所有方法都使用相同的训练和在线适应策略。
在这里插入图片描述

图 1：在线集成的激励示例，其中报告的指标是 MSE，在线适应期间预测范围长度设置为 48。跨时间是指假设协变量之间独立且仅对时间依赖性进行建模的 TCN 主干，而交叉变量是指考虑跨变量依赖性的 TCN 主干。

尽管变量独立性增强了模型的稳健性，但跨变量依赖性对于预测也至关重要，即对于特定变量，来自其他变量中关联序列的信息可能会改善预测结果。如表 1 中数据集 ETTm1 和 ETTh2 所示，跨时间预测器对于变量数量较少的数据集往往会产生较低的性能。令人惊讶的是，旨在利用跨变量和跨时间依赖关系的现有模型（例如 CrossFormer [Zhang 和 Yan，2023] 和 TS-Mixer [Chen 等人，2023]）的性能往往比原生 TCN 更差。为了研究这一现象，我们在图 1 中对跨时间模型 (Time-TCN) 和跨变量模型 (TCN) 的整个在线适应过程中不同时间步的 MSE 进行了可视化。我们观察到 MSE 超过在线适应，表明随着时间的推移，概念发生了重大漂移。我们还观察到，这两种方法的表现都始终优于另一种，这表明这两种数据假设都不适用于整个时间序列。这就是为什么依靠像 CrossFormer 这样的单一模型无法解决这个问题。现有的工作依赖于简单的模型，但对于在线时间序列预测，模型偏差的数据偏好将随着在线概念漂移而不断变化。因此，我们需要一种依赖数据的策略来不断改变模型选择策略。换句话说，在线时间序列预测应该超越参数更新。

在本文中，我们通过引入共享不同数据偏差的模型集合来解决在线时间序列预测的单一模型的局限性。然后，我们学习动态组合各个模型的预测以获得更好的预测。通过允许每个模型独立训练和在线更新，我们可以充分利用每个在线模型；通过动态调整不同模型的组合，我们可以充分利用整个模型集成。我们将我们的方法称为在线集成网络或简称 OneNet。更具体地说，OneNet 维护两种在线预测模型，一种专注于建模时间相关性，另一种专注于建模跨变量依赖性。每个模型都使用同一组训练数据进行独立训练。在测试过程中，开发了基于强化学习（RL）的方法来动态调整用于组合两个模型的预测的权重。与指数梯度下降等经典在线学习方法相比，我们基于强化学习的方法能够更有效地适应概念的变化/漂移，从而获得更好的性能。本文的贡献是：

我们介绍 OneNet，这是一种用于在线时间序列预测的双流架构，它使用在线凸规划集成了两个模型的输出。 OneNet 利用变量无关模型的鲁棒性来处理概念漂移，同时捕获不同变量之间的相互依赖性以提高预测准确性。此外，我们提出了一种基于强化学习的在线学习方法，以减轻传统 OCP 算法的局限性，并通过实证和理论分析证明其有效性。
我们对四个数据集的实证研究表明，与最先进的方法相比，OneNet 将平均累积均方误差（MSE）降低了 53.1%，平均绝对误差（MAE）降低了 34.5%。特别是，在具有挑战性的数据集 ECL 上的性能增益非常出色，MSE 降低了 59.2%，MAE 降低了 63.0%。
我们进行了全面的实证研究，以调查预测模型的常用设计选择（例如实例归一化、变量独立性、季节趋势分解和频域增强）如何影响模型的稳健性。此外，我们系统地比较了现有基于 Transformer 的模型、基于 TCN 的模型和基于 MLP 的模型在面临概念漂移时的鲁棒性。

二、前期及相关工作

概念漂移。现实世界中的概念通常是动态的，并且会随着时间的推移而变化，对于天气预报和客户偏好等场景尤其如此。由于底层数据分布的未知变化，从历史数据中学习的模型可能会与新数据不一致，因此需要定期更新以保持准确性。这种现象被称为概念漂移 [Tsymbal, 2004]，它增加了从数据中学习模型的过程的复杂性。在本文中，我们重点关注时间序列预测的在线学习。与大多数现有的在线时间序列预测研究[Li et al., 2022, Qing et al., 2022, Pham et al., 2023]不同，该研究仅关注如何在线更新模型，这项工作超越了参数更新并引入了多个模型和可学习的集成权重，产生丰富且灵活的假设空间。由于篇幅限制，更多关于时间序列预测和强化学习的相关工作留在附录中。

在线时间序列预测：流数据。传统的时间序列预测任务具有回溯窗口 L 的多元时间序列的集合： $L\colon(\mathbf{x}_i)_{i=1}^L$ ，其中每个 $x_i$ 是 M 通道向量 $\mathbf{x}_i=(x_i^j)_{j=1}^M$ 。给定预测范围 H，目标是预测 H 个未来值 $(\mathbf{x}_{i})_{i=L+1}^{L+H}$ 。在实际应用中，建立在历史数据之上的模型需要预测未来的数据，即给定时间偏移量 $K'>L,\text{ and }(\mathbf{x}_i)_{i=K'-L+1}^{K'},$ ，模型需要：预测 $(\mathbf{x})_{i=K'+1}^{K'+H}$ 。由于数据的连续性和概念的频繁漂移，在线时间序列预测 [Anava et al., 2013, Liu et al., 2016, Pham et al., 2023] 是现实世界中广泛使用的技术。在这种方法中，学习过程发生在一系列轮次中，其中模型接收回顾窗口并预测预测窗口。然后揭示真实值，以提高模型在下一轮中的性能。当我们执行在线适应时，使用在线数据流重新训练模型，每个通道上都有 MSE 损失： $\mathcal{L}=\frac1M\sum_{j=1}^M\parallel\hat{x}_{K^{\prime}+1:K^{\prime}+H}^j-x_{K^{\prime}+1:K^{\prime}+H}^j\parallel$ 。

与变量无关的时间序列预测。大多数结构中使用的传统跨变量策略将所有时间序列特征的向量作为输入，并将其投影到嵌入空间中以混合信息。相反，PatchTST [Nie et al., 2023] 采用与变量无关的方法，其中每个输入标记仅包含来自单个通道/变量的信息。我们的研究表明，变量独立性对于提高概念漂移下模型的鲁棒性至关重要。对于多元时间序列样本 $x_i^j)_{i=1}^L$ ，每个通道j独立地输入到模型中，预测器相应地产生预测结果 $x_{i}^{j})_{i=L+1}^{L+H}$ 。如表1所示，当数据集变量较多时，跨变量方法容易出现过拟合，导致性能不佳。这一点在 ECL 数据集中的 SOTA 在线适应模型 FSNet [Pham et al., 2023] 的糟糕表现中得到了体现。然而，缺乏跨变量信息的模型在具有少量变量的数据集上表现较差，其中跨变量依赖性可能是必不可少的。尽管一些现有的工作试图将跨变量交互和时间依赖性合并到一个框架中，但我们的实验表明，这些模型在概念漂移的情况下很脆弱，并且表现并不比提出的简单基线 Time-TCN 更好。为了解决这个问题，我们提出了一种新的方法来训练两个独立的分支，每个分支分别专注于建模时间和跨变量依赖关系。然后，我们结合这些分支的结果，以在概念漂移下获得更好的预测性能。我们首先引入 OCP 块以实现一致性。
在这里插入图片描述
图 2：(a) OneNet 通过跨时间和跨变量分支处理多变量数据，每个分支负责捕获不同的方面。这两个分支的权重由 OCP 块生成，只有黑色箭头需要在训练期间执行。 (b) OCP 块通过利用指数梯度下降 (EGD) 的长期历史和离线强化学习 (RL) 的短期历史来生成集成权重。

三、 OneNet: Ensemble Learning for Online Time Series Forecasting

我们首先研究在线学习方法来动态调整集成学习使用的组合权重。然后我们提出 OneNet，一个用于在线时间序列预测的集成学习框架。

3.1 Learning the best expert by Online Convex （凸）Programming (OCP)

为了符号清楚起见，这里我们将 $\mathbf{x}\in\mathbb{R}^{L\times M}$ 表示为历史数据， $\mathbf{y}\in\mathbb{R}^{H\times M}$ 表示为预测目标。我们当前的方法涉及多个互补模型的集成。因此，如何更好地将模型预测集成到在线学习环境中是一个重要问题。指数梯度下降 (EGD) [Hill 和 Williamson, 2001] 是一种常用的方法。具体来说，决策空间 △ 是一个 d 维单纯形，即 $\triangle=\{\mathbf{w}_{t}|w_{t,i}\geq0\text{ and }\parallel\mathbf{w}_{t}\parallel_{1}=1\}$ ，其中 t 是时间步长指示器，为简单起见，当它为不混乱。给定在线数据流 x、其预测目标 y 以及具有不同参数 $\mathbf{f}=[\tilde{\mathbf{y}}_{i}=f_{i}(\mathbf{x})]_{i=1}^{d}$ 的 d 个预测专家，玩家的目标是最小化预测误差：

在这里插入图片描述
根据EGD，选择 $\textbf{w}_{1}=[w_{1,i}=1/d]_{i=1}^{d}$ 作为单纯形的中心点，并将 $\ell_{t,i}$ 表示为 $f_i$ 在时间步t的损失，每个 $w_i$ 的更新规则为

在这里插入图片描述

其中 $Z_{t}=\sum_{i=1}^{d}w_{t,i}\exp(-\eta l_{t,i})$ 是归一化器，并且该算法具有遗憾界限：

命题 1.（在线凸规划界）对于 T > 2 log(d)，设 $\textit{step t}=1,\ldots,T\textit{ as }R(T),\textit{set }\eta=\surd2\operatorname{log}(d)/T$ ，OCP 更新策略存在外部遗憾（证明和分析见附录 B.1）。

在这里插入图片描述也就是说，指数加权平均预测器保证预测器的累积预期损失不会比最佳决策的累积损失大很多。然而，众所周知，指数加权平均预测器对分布的剧烈变化的响应非常缓慢[Cesa-Bianchi 和 Lugosi，2006]。这种现象有时在在线学习文献中被称为“慢切换现象”，并在图 3 中得到进一步说明，其中 f1 的损失在前 50 次试验中为 0，在接下来的 50 次试验中为 1。 f2的表现则相反。当步长 η 较小时（例如 η = 0.01），权重发生微小变化，并且不会发生明显的适应。当应用大步长 η（例如 η = 1）时，我们观察到 EGD 算法通过在前几次迭代中将权重 w1 增加到几乎 1，快速适应前 50 次试验的环境变化。但EGD算法需要多次迭代才能适应接下来50次迭代的变化，其中f2的效果比f1好得多。最后我们注意到，无论我们如何调整步长 η，EGD 算法都必须在整个范围内的切换速度和整体良好性能之间进行权衡。

尽管很少有人开发出算法来解决在线学习中的这个问题[Stoltz and Lugosi, 2005, Cesa-Bianchi and Lugosi, 2003, Blum and Mansour, 2007, Foster and Vohra, 1998]，但关键思想是找到一个激活函数根据最近失去的所有专家，将原始策略 wt 映射到新策略 wt。尽管付出了努力，无论是在经验上还是在理论上，所取得的成功都非常有限。在这项工作中，我们在实验中观察到，EGD 算法生成的组合权重 w 是基于很长一段时间内的历史性能，因此无法快速适应瞬态环境变化。因此，最好有效地将长期历史信息和最近的环境变化结合起来。一个简单的想法是重新初始化每 K 步的权重 w。我们证明这样一个简单的算法可以实现更紧密的界限：

在这里插入图片描述
图 3：分配给 f1 的权重的演变，其中预测者的损失在第一个状态 [0, 50] 和第二个状态 [50, 100] 中变化。

命题 2.（非正式）将 I = [l, · · · , r] ∈ [1, · · · , T] 表示为任意时间段。然后我们发现，与 EGD 相比，K 步重新初始化算法在任何小间隔 I 处都有更严格的后悔界限，其中 |I| < $T^{\frac34}$ 。（证明见附录B.2。）

命题2强调，通过考虑短期信息，我们可以在短时间内获得较低的后悔。这样一个简单的策略仍然在K的超参数选择上遇到困难。此外，丢弃长期信息使得该算法在长时间的在线学习过程中不如EGD。在这项工作中，我们通过利用离线强化学习来应对在线学习的这一挑战[Levine et al., 2020]。首先，我们使用EGD来维持长期体重w。此外，我们引入了一组不同的权重b，可以更好地捕捉各个模型的近期表现。通过结合 w 和 b，我们的方法可以有效地结合长期历史信息和最近的环境变化。

具体来说，我们采用 RvS [Emmons et al., 2022] 框架，该框架通过监督学习制定强化学习，如图 2(b) 所示。在时间步 t，我们的目标是学习以长期权重 w 和专家在短期历史时期 I = [l, t] 中的表现为条件的短期权重。为了简单性和计算效率，我们只让 l = t − 1。然后代理使用策略 $\pi_{\theta_{rl}}\left(\mathbf{b}_{t}|\{\{w_{t,i}\tilde{y}_{i}\}_{i=1}^{d}\}_{t\in I};\mathbf{y}\right)$ 选择动作； y 由 θrl 参数化。在训练过程中，我们将每个预测和专家权重 $(w_{t,i}*\tilde{\mathbf{y}}_i)$ 之间的乘积与结果 y 连接起来作为条件输入。我们遵循 RvS [Emmons et al., 2022] 将策略网络实现为两层 MLP $\begin{aligned}f_{rl}:\mathbb{R}^{H\times M\times(d+1)}\to\mathbb{R}^d\end{aligned}$ 。那么短期权重和最终集成权重将是：

在这里插入图片描述
然而，与 RvS 不同，我们无法通过简单的分类任务来训练决策网络，因为地面真实目标动作是不可访问的。相反，我们建议通过最小化新权重产生的预测误差来训练网络，即 $\min_{\theta_{rl}}\mathcal{L}(\tilde{\mathbf{w}}):=\parallel\sum_{i=1}^d\tilde{w}_{t,i}f_i(\mathbf{x})-\mathbf{y}\parallel^2.$ 。在推理过程中，随着概念漂移逐渐变化，我们使用 wt−1 + bt−1 来生成预测，并在观察到真实结果后训练网络。我们从理论上和经验上验证了附录 B.4 中提出的 OCP 块的有效性。

3.2 OneNet: utilizing the advantages of both structures

模型结构如图2(a)所示，各组成部分介绍如下：

Two-stream forecasters。输入的多元时间序列数据被输入两个单独的预测器，即跨时间预测器 f1 和跨变量预测器 f2。每个预测器包含一个编码器和一个预测头。假设模型的隐藏维度均为 dm ，f1 的编码器将输入序列投影为表示 $\begin{aligned}z_1\in\mathbb{R}^{M\times d_m}\end{aligned}$ ，预测头生成最终的预测结果： $\tilde{\mathbf{y}_1}\in\mathbb{R}^{M\times H}$ 。对于跨变量预测器 f2，编码器将 x 投影到 $\mathbf{z}_{2}\in\mathbb{R}^{L\times d_{m}}$ 。然后，选择最后一个时间步的表示 $\mathbf{z}_{2,L}\in\mathbb{R}^{d_{m}}$ 并将其输入到预测头中，以生成最终的预测结果 $\tilde{\mathbf{y}_2}\in\mathbb{R}^{M\times H}$ 。与f1的投影头参数为dm×H相比，f2的投影头参数为dm×M×H，较重，尤其是当M较大时。此外，虽然 f1 忽略变量依赖性，但 f2 只是选择最后一个时间步时间序列的表示，忽略时间依赖性。这两个模块为预测任务产生不同但互补的归纳偏差。然后使用 OCP 块来学习最佳组合权重。具体来说，我们使用 EGD 更新每个预测器的权重 wi ，并使用离线强化学习学习额外的短期权重 bi ，一个预测器的最终组合权重将是 $w_{i}\leftarrow w_{i}+b_{i}$ 。考虑到变量之间的差异，我们进一步为每个变量构造不同的权重，即我们将有 $\mathbf{w}\in\mathbb{R}^{M\times2}$ 组合权重。

解耦的训练策略。 OneNet 的一个简单的训练策略是最小化 OCP 块和两个预测器的 $\mathcal{L}(w_{1}*\tilde{\mathbf{y}_1}+w_2*\tilde{\mathbf{y}_2},\mathbf{y})$ ，其中 wi 这里表示带有附加偏差项的权重。然而，耦合训练策略有一个致命的缺陷：考虑到极端情况，即 f1 总是比 f2 表现得好得多，那么 w1 将接近 1，w2 → 0。在这种情况下， $\nabla_{\tilde{\mathbf{y}_2}}\mathcal{L}(w_1*\tilde{\mathbf{y}_1}+w_2*\tilde{\mathbf{y}_2},\mathbf{y})\approx0$ ，即f2很可能没有被训练很长时间。在概念漂移的背景下，如果不进行再训练，随着时间的推移，f2的性能将变得较差。因此，在本文中，我们将 OCP 模块和两个预测器的训练过程解耦。具体来说，两个预测器由 $\mathcal{L}(\tilde{\mathbf{y}_1},\mathbf{y})+\mathcal{L}(\tilde{\mathbf{y}_2},\mathbf{y})$ 训练，OCP 块由 $\begin{aligned}\mathcal{L}(w_1*\tilde{\mathbf{y}_1}+w_2*\tilde{\mathbf{y}_2},\mathbf{y})\end{aligned}$ 训练。

备注请注意，OneNet 是对时间序列预测和概念漂移下在线自适应方法的先进架构的补充。更强的主干或更好的适应策略/结构都可以提高性能。

四、 Experiments

在本节中，我们将展示：（1）所提出的 OneNet 仅通过简单的再训练策略就获得了优异的预测性能（与之前的 SOTA 模型相比，MSE 降低了 50% 以上）；（2）OneNet比其他方法实现更快更好的收敛； (3)我们进行彻底的消融研究和分析，以揭示当前先进预测模型的每个设计选择的重要性。最后，我们引入了 OneNet 的一个变体，称为 OneNet-，它的参数明显更少，但仍然大幅优于之前的 SOTA 模型。由于篇幅限制，附录中提供了一些实验设置和结果。
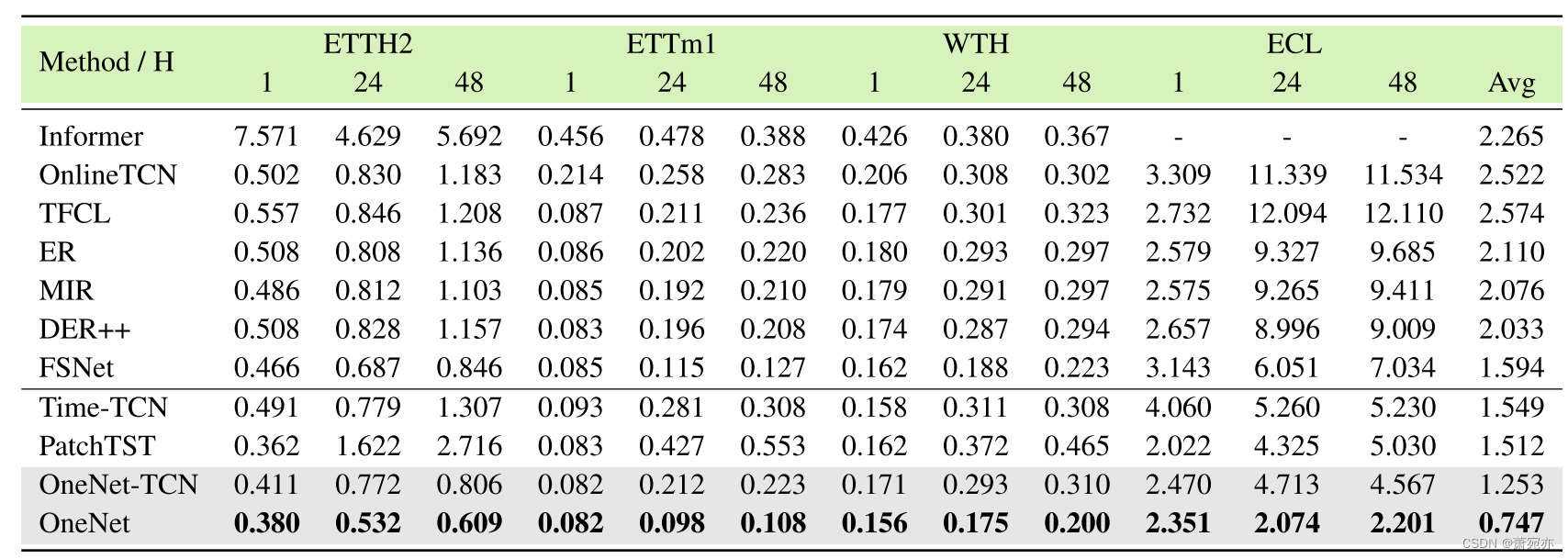
表2：各种适应方法的MSE。 H：预测范围。 OneNet-TCN是TCN和Time-TCN的混合，OneNet是FSNet和Time-FSNet的混合。
在这里插入图片描述

4.1 Experimental setting

适应方法的基线我们评估了实验的几个基线，包括持续学习、时间序列预测和在线学习的方法。我们的第一个基线是 OnlineTCN [Zinkevich, 2003]，它在没有任何特定策略的情况下持续训练模型。第二个基线是体验重播 (ER) [Chaudhry et al., 2019]，其中先前的数据存储在缓冲区中，并在学习过程中与新样本交错。此外，我们考虑了 ER 的三种高级变体：TFCL [Aljundi et al., 2019b]，它使用任务边界检测机制和知识整合策略； MIR [Aljundi et al., 2019a]，选择导致遗忘最多的样本； DER++ [Buzzega et al., 2020]，它结合了知识蒸馏策略。值得注意的是，ER 及其变体是在线环境中的强大基线，因为我们在训练期间利用小批量来减少单个样本的噪声并实现更快更好的收敛。最后，我们将我们的方法与 FSNet [Pham et al., 2023] 进行比较，后者是之前最先进的在线适应方法。考虑到不同的模型结构，我们比较了各种结构在概念漂移下的性能，包括TCN [Bai et al., 2018]、Informer [Zhou et al., 2021]、FEDformer [Zhou et al., 2022b]、PatchTST [Nie] 等人，2023]、D线性[Zeng 等人，2023]、N线性[Zeng 等人，2023]、TS-Mixer [Chen 等人，2023]。

强大的集成基线。为了验证所提出的 OCP 块的有效性，我们将其与几个集成基线进行了比较。给定在线输入x，每个专家的预测 $\tilde{\mathbf{y}_{1}},\tilde{\mathbf{y}_{2}}$ ，以及真实结果y，不同基线的最终结果~y将如下：（1）简单平均：我们简单地对两位专家共同得出最终预测，即 $\tilde{\mathbf{y}}=\frac{1}{2}(\tilde{\mathbf{y}_{1}}+\tilde{\mathbf{y}_{2}})$ 。 (2)门控机制Liu et al. [2021]：我们学习每个预测器输出的权重，即 $h=\mathbf{W}Concat(\tilde{y_{1}},\tilde{y_{2}})+\mathbf{b};w_{1},w_{2}=softmax(h)$ ，最终结果由 $\begin{aligned}\tilde{\mathbf{y}}=w_1*\tilde{y_1}+w_2*\tilde{y_2}\end{aligned}$ 给出。 (3) 专家混合Jacobs 等人。 [1991]，沙泽尔等人。 [2017]：我们使用专家混合方法，首先通过对输入的线性组合应用 softmax 函数来学习权重 w1 和 w2，即 h = Wx+ b； w1, w2 = softmax(h)，然后我们通过组合两位专家的预测来获得最终预测： $\tilde{\mathbf{y}}=w_{1}*\tilde{y_{1}}+w_{2}*\tilde{y_{2}}$ 。 (4)线性回归(LR)：我们使用简单的线性回归模型来获得最佳权重，即 $[w_{1},w_{2}]=(X^{T}X)^{-1}X^{T}y,\mathrm{where~}\bar{X}=[\tilde{\mathbf{y}_{1}},\tilde{\mathbf{y}_{2}}]$ 并且y是地面真实结果。 (5)指数梯度下降(EGD)：我们使用EGD分别更新权重w1和w2，而没有额外的偏差。 (6) 强化学习直接学习权重（RL-W）：我们使用OCP块中的偏差项根据专家的预测和地面真实结果来更新权重，即权重仅依赖于 $\tilde{\mathbf{y}_1},\tilde{\mathbf{y}_2},$ 和 y，但不是每个专家的历史表现。对于所有具有可训练参数的基线，训练过程与建议的 OCP 块相同。

4.2 Online forecasting results

累积性能表 2 和表 3 以均方误差 (MSE) 和平均绝对误差 (MAE) 的形式呈现了不同基线的累积性能。特别是，Time-TCN 和 PatchTST 表现出强大的性能，并且优于之前最先进的模型 FSNet [Pham et al., 2023]。所提出的 OneNet-TCN（TCN 和 Time TCN 的在线集成）超越了各种预测范围内的大多数竞争基线。有趣的是，如果组合的分支更强，例如 OneNet 结合了 FSNet 和 Time-FSNet，取得了比 OneNet-TCN 更好的性能。也就是说，OneNet可以集成任何先进的在线预测方法或表示学习结构，以增强模型的鲁棒性。 OneNet 的平均 MSE 和 MAE 明显优于单独使用任一分支（FSNet 或 Time-TCN），这强调了合并在线集成的重要性。

在这里插入图片描述

在这里插入图片描述
与强集成基线的比较如表 4 所示。与仅使用平均等简单集成方法的 FSNet 相比，两分支框架极大地提高了性能。从输入 x 中学习权重的 MOE 方法表现不佳，甚至不如简单地平均预测结果。另一方面，从 $\tilde{\mathbf{y}_1}\text{ and }\tilde{\mathbf{y}_2}$ （门控）的预测结果中学习权重，其性能比 MOE 好得多。这表明组合权重应取决于模型预测。然而，由于在线数据流的稀缺性和学习权重的高噪声，将学习问题表述为线性回归并使用封闭式解决方案并不是一个好主意。与平均方法相比，EGD 提供了显着的优势，这凸显了每位专家累积历史表现的重要性。此外，我们观察到 RL-W 在某些数据集上实现了与 EGD 相当甚至更好的性能。因此，我们提出 OCP 模块，使用 EGD 更新长期权重，使用离线 RL 学习短期权重。与所有其他基线相比，这种设计带来了卓越的性能。

预测结果如图 4 所示。与难以适应新概念并产生较差预测结果的基线相比，OneNet 可以成功捕获时间序列的模式。更多可视化结果和收敛分析见附录 C.7。

4.3 Ablation studies and analysis

实例归一化和季节趋势分解的效果如表所示。 5. 结果表明，无论模型是否在线适应，从 PatchTST 中删除季节性趋势分解组件效果有限。实例归一化通常用于减轻训练数据和测试数据之间的分布变化，这对于在线适应不可能时的模型鲁棒性至关重要。然而，当进行在线适应时，实例归一化的影响会减小。有趣的是，我们的实验表明，当预测范围较长（24 或 48）时，实例归一化会阻碍 ETTH2、ETTm1 和 WTH 数据集中的模型适应过程。因此，简单地用零均值和单位标准差标准化时间序列可能不是概念漂移下的最佳方法。附录中详细介绍了变量独立性和频域增强的消融研究。

在这里插入图片描述
图 4：在线学习期间模型的预测和参数可视化。 (a) 具有不同预测范围的 ECL 数据集上不同模型的参数数量。我们专注于从 t = 2500 开始的短 50 时间步长范围。(b) 和 © 描述了模型对 ECL 数据集的第一和第二通道的预测结果。

表 5：非适应 PatchTST 和在线适应 PatchTST 的实例归一化 (inv) 和季节性趋势分解 (Decomp) 的消融研究，其中度量为 MSE。

在这里插入图片描述深入研究参数高效的在线适应。虽然 OneNet 显着降低了预测误差，但由于其双流框架，它也增加了参数数量和推理时间。我们还设计了 OneNet 的一个变体，其性能可能比 OneNet 稍低，但参数较少，使其更适合轻量级应用，记为 OneNet-。具体来说，我们集成了 PatchTST 和 Time-FSNet，它们都是变量无关的。在这种情况下，将 z1、z2 表示为来自两个分支的一个变量的生成特征，我们将这两个特征连接起来并将它们输入到投影头中，这进一步避免了用于集成权重学习的离线强化学习块并减少了参数。例如，在 ECL 数据集中，隐藏维度 FSNet [Pham et al., 2023] 为 320，序列有 321 个通道。当预测范围为 48 时，投影头仅由一个线性层组成，具有 320 × 321 × 48 = 4, 930, 560 个参数。相反，OneNet-的级联特征总是小于1024维，导致最终的投影头少于1024×48=49，152个参数。图 4(a) 显示了 ECL 数据集上不同方法的详细比较。对于较小的预测范围，所有方法都具有相当数量的参数。随着预测范围的增加，现有适应方法的参数数量迅速增加。相反，OneNet-的参数数量对预测范围不敏感，并且始终小于所有基线。 OneNet-的性能如表12所示，它比FSNet好得多，但实现的参数更少。

不同预测模型的比较和更多数值结果，例如不同超参数的详细消融研究和更多设置下的适应结果，请参见附录。

五、 Conclusion and Future Work

通过对具有概念漂移的高级预测模型行为的研究，我们发现跨时间模型在变量数量较多时表现出更大的鲁棒性，但不如在变量数量较少时建模变量依赖性的模型。此外，由于概念漂移的发生，这个问题变得更具挑战性，因为两种模型偏差的数据偏好在整个在线预测过程中都在动态变化，使得单一模型难以克服。为此，我们提出了 OneNet 模型，它通过 OCP 充分利用了两种模型的优点。此外，我们建议通过离线强化学习学习额外的短期权重，以减轻传统策略学习算法中常见的慢切换现象。我们大量的实验表明，OneNet 能够有效地处理各种类型的概念漂移，并且在预测性能方面优于以前的方法。

我们还发现实例归一化增强了模型在概念漂移下的鲁棒性，但可能会阻碍模型在某些场景下快速适应新分布的能力。这促使人们进一步探索是否存在一种标准化技术，可以减轻分布变化，同时能够快速适应不断变化的概念。此外，虽然我们设计了 OneNet 的轻量化版本来解决引入额外参数和推理时间的问题，但仍有可能采用更有效的适应方法，例如利用 NLP/CV 社区的提示和高效调整方法，以避免重新训练完整模型。