典型随机噪声激励

Luister.

已于 2023-05-11 08:48:49 修改

阅读量3k

点赞数 1

文章标签：学习

于 2023-05-10 21:28:04 首次发布

本文链接：https://blog.csdn.net/weixin_45774613/article/details/130500057

版权

1.按噪声的起源分类

根据噪声的起源，分为内部噪声和外部噪声。
内部噪声：来源于系统内部的涨落运动或被检测信号，如布朗粒子受到周围液体分子的无规则碰撞即为内部噪声；
外部噪声：来自系统所处外部环境的随机涨落，或由外部参量控制的随机涨落，反映外界因素对系统的影响和扰动，如环境温度的变化、电子设备的磁场、脉冲激光、广播信号、雷达发射等。

根据噪声引入系统的方式，分为加性(或外激)噪声和乘性噪声(或参激）噪声。
加性噪声：一般视为系统的背景噪声，主要来源包括内部噪声、自然噪声和人为噪声。
乘性噪声：在系统中表现出与系统变量相乘的关系，通常是由系统的时变性或非线性造成的，其中系统的扩散系数表现为状态变量的函数项，且外部噪声一般视作乘性噪声。

加性噪声和乘性噪声，无论起源是否相同，两噪声之间都可能存在一定的互关联性。
噪声间的互关联性通常有两种形式：一种是δ函数相关形式，另一种是e指数形式。
对于互关联噪声驱动的非线性系统，通常需要借助变换法或泛函近似法先消除噪声之间的互关联性，然后再推导其相应的Fokker-Planck方程。

2.按噪声的功率谱密度分类

根据功率谱密度的不同，噪声可以分为白噪声和色噪声。
白噪声的功率谱密度为常数，具有零相关时间，常见的白噪声类型有高斯白噪声和泊松白噪声；
色噪声的功率谱密度依赖于频率的变化，存在非零相关时间，如高斯色噪声和多值噪声。
特别地，高斯噪声的概率密度服从高斯分布，由于高斯噪声是平稳随机过程，完全由均值和相关函数确定，为便于分析和计算，在随机动力学的研究中普遍采用高斯噪声。

3.功率谱密度

区别于密度，功率谱密度积分不为1，故一般需要对其进行无量纲化（归一化）。
功率谱密度为相关函数的傅里叶变换。

4.高斯白噪声模拟

高斯白噪声 $\xi(t)$ 定义为维纳过程的形式导数，其均值和相关函数为： $\left \langle \xi(t) \right \rangle=0$ , $\left \langle \xi(t)\xi({t}') \right \rangle=2D\delta (t-{t}')$ ;则功率谱密度为： $S(\omega )=\int_{-\infty }^{\infty }2D\delta ({\tau }')e^{-i\omega {\tau }'}d{\tau }'=2D$ ,由此可见，高斯白噪声的功率谱密度 $S(\omega)$ 与频率 $\omega$ 无关。
在随机振动理论中，为简化计算，通常将宽带或记忆时间很短的随机模型近似为白噪声。

两种高斯白噪声的数值模拟方法(以MATLAB为例）：
1.产生一个标准的正态分布，即X~N(0,1)，构造高斯白噪声: $\xi_{k}=\sqrt{2D/\Delta t}X_{k}(k=1,2,...)$ ,其中 $\Delta t$ 是时间步长
2.产生(0,1)之间两个相互独立的均匀分布，即 $Y^{(1)}\sim U(0,1),Y^{(2)}\sim U(0,1)$ ;
构造满足标准正态分布的随机数： $Z_{k}^{(1)}=\sqrt{-2lnY_{k}^{(1)}}cos(2\pi Y_{k}^{(2)})$ 和 $Z_{k}^{(2)}=\sqrt{-2lnY_{k}^{(1)}}sin(2\pi Y_{k}^{(2)})$ ;
构造两个相互独立的高斯白噪声: $\xi _{k}^{(1)}=\sqrt{2D/\Delta t}Z_{k}^{(1)}$ 和 $\xi _{k}^{(2)}=\sqrt{2D/\Delta t}Z_{k}^{(2)}$ .

如果两个高斯白噪声 $\xi^{(1)}$ 和 $\xi^{(2)}$ 存在互关联性，满足如下统计性质：
$\left \langle \xi^{(1)}(t) \right \rangle=\left \langle \xi^{(2)}(t) \right \rangle=0$
$\left \langle \xi^{(1)}(t)\xi^{(1)}({t}') \right \rangle=2D_{1}\delta(t-{t}'),\left \langle \xi^{(2)}(t)\xi^{(2)}({t}') \right \rangle=2D_{2}\delta(t-{t}')$
$\left \langle \xi^{(1)}(t)\xi^{(2)}({t}') \right \rangle=\left \langle \xi^{(1)}({t}')\xi^{(2)}(t) \right \rangle=2\lambda \sqrt{(D_{1}D_{2})}\delta(t-{t}')$
其中， $\lambda$ 表示噪声 $\xi^{(1)}$ 和 $\xi^{(2)}$ 之间的互关联强度。
为数值模拟产生关联噪声，先利用上面的方法产生两个独立的高斯随机数 $W_{1}$ 和 $W_{2}$ ，再构造下列形式即可
$\xi^{(1)}=\sqrt{2D_{1}/\Delta t}W_{1}$ , $\xi^{(2)}=\sqrt{2D_{2}/\Delta t}(\lambda W_{1}+\sqrt{1-\lambda ^{2}W_{2}})$ .

%%
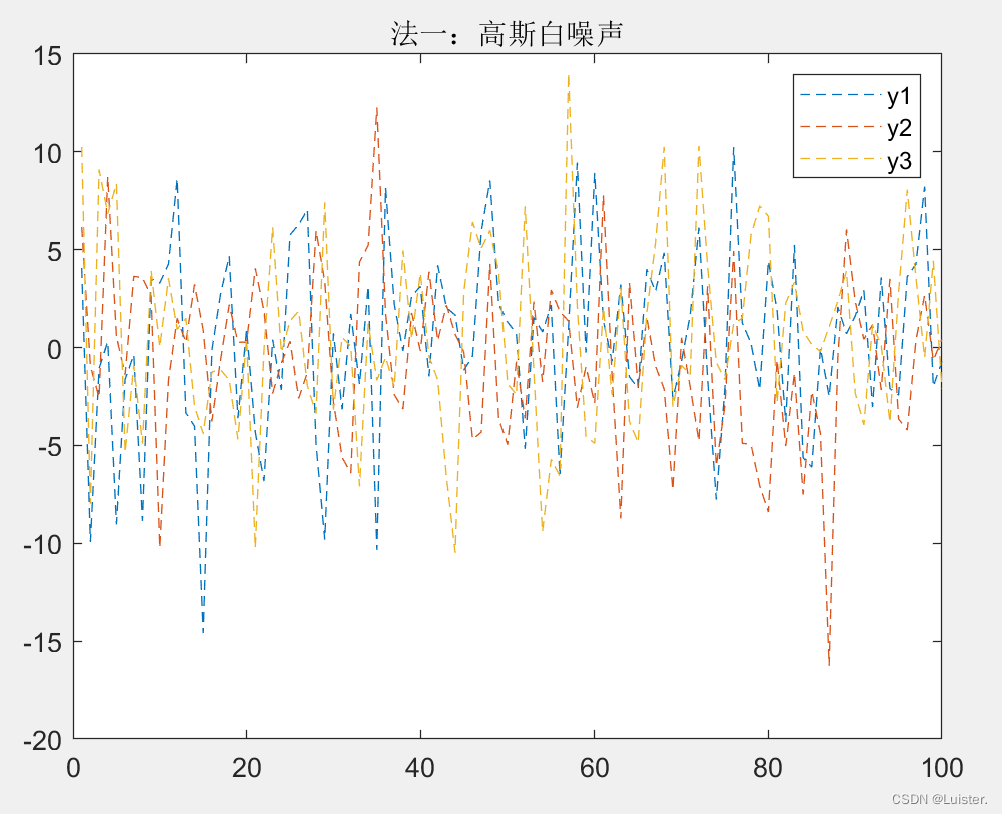
%高斯白噪声模拟
%法1：
clc;clear;
D=1;
delta_t=0.1;
N=3;
legendStrings = strings(1, N);
% randn('state',100);
for k=1:N
    X(k,:)=randn(100,1);
    xi(k,:)=sqrt(2*D/delta_t)*X(k,:);
    plot(xi(k,:),'--')
    hold on
    legendStrings(k) = sprintf('y%d', k);
    hold on
end
hold off
legend(legendStrings);
title("法一：高斯白噪声")
%%
%法二：
clc;clear;
D=1;
delta_t=0.1;
N=3;
legendStrings = strings(2, N);
randn('state',100);
for k=1:N
    Y1(k,:)=rand(100,1);
    Y2(k,:)=rand(100,1);
    Z1(k,:)=sqrt(-2*log(Y1(k,:))).*cos(2*pi*Y2(k,:));
    Z2(k,:)=sqrt(-2*log(Y1(k,:))).*sin(2*pi*Y2(k,:));
    xi1(k,:)=sqrt(2*D/delta_t)*Z1(k,:);
    xi2(k,:)=sqrt(2*D/delta_t)*Z2(k,:);
    plot(xi1(k,:),'--')
    legendStrings(1,k) = sprintf('y%d', k);
    hold on
    plot(xi2(k,:),'*-')
    legendStrings(2,k) = sprintf('y%d', k);
    hold on
end
hold off
legend(legendStrings);
title("法二：高斯白噪声")

在这里插入图片描述

%%
%数值模拟产生关联噪声
clc;clear;
D=1;
delta_t=0.1;
N=3;
legendStrings = strings(2, N);
randn('state',100);
lambda=0.8;%噪声间的互关联强度
D1=1.1;
D2=0.9;
for k=1:N
    Y1(k,:)=rand(100,1);
    Y2(k,:)=rand(100,1);
    W1(k,:)=sqrt(-2*log(Y1(k,:))).*cos(2*pi*Y2(k,:));
    W2(k,:)=sqrt(-2*log(Y1(k,:))).*sin(2*pi*Y2(k,:));
    xi1(k,:)=sqrt(2*D1/delta_t)*W1(k,:);
    xi2(k,:)=sqrt(2*D2/delta_t)*(lambda*W1(k,:)+sqrt(1-lambda^2)*W2(k,:));
    plot(xi1(k,:),'--')
    legendStrings(1,k) = sprintf('y%d', k);
    hold on
    plot(xi2(k,:),'*-')
    legendStrings(2,k) = sprintf('y%d', k);
    hold on
end
hold off
legend(legendStrings);
title(sprintf("互关联强度为%0.1f的高斯白噪声",lambda))

在这里插入图片描述

5.高斯色噪声模拟

高斯色噪声 $\eta(t)$ 是指数型色噪声，也称为Ornstein-Uhlenbeck,OU噪声，通常满足如下随机微分方程：
$\dot{\eta}(t)=-\frac{\eta(t)}{\tau }+\frac{\xi(t)}{\tau }$ ，其中 $\tau$ 是噪声相关时间， $\xi(t)$ 是具有零均值的高斯白噪声。
由此得到 $\eta(t)$ 对应的平稳概率密度： $P_{s}(\eta)=\frac{1}{\sqrt{(2\pi D{\tau}')}}exp(-\frac{\tau}{2D}\eta^2)$ ；
对应的统计特性： $\left \langle \eta(t) \right \rangle=0$ , $\left \langle \eta(t)\eta({t}') \right \rangle=\frac{D}{\tau}exp(-\frac{\left |t-{t}' \right |}{\tau})$ ,该式说明噪声相关事件仅依赖于时间差，具有平稳过程的性质，通过对其相关函数进行傅里叶变换可得到指数型噪声的功率谱为 $S(\omega)=\frac{2D}{1+\tau^2 \omega^2}$ , $S(\omega)$ 具有洛伦兹谱的形式，当相关时间 $\tau$ 很小时，趋近于0，此时高斯色噪声就退化成为高斯白噪声。
色噪声中的相关时间包含对历史的记忆，这一过程是非马尔可夫过程，但是通过各种近似方法对高斯色噪声进行近似处理，如统一色噪声近似、最速下降法以及弱噪声展开法等。

根据一阶随机微分方程 $\dot{\eta}(t)=-\frac{\eta(t)}{\tau }+\frac{\xi(t)}{\tau }$ ，可以通过随机四阶龙格库塔方法数值模拟得到高斯色噪声 $\eta(t)$
具体计算公式为： $\eta(t+\Delta t)=\eta(t)+\frac{1}{6}\Delta t(H_{1}+2H_{2}+2H_{3}+H_{4})+\sqrt{\frac{D\Delta t}{\tau^2}}(\psi_1+\psi_2)$
其中， $\psi_i(i=1,2)$ 是高斯随机数且满足 $\left \langle \psi_i \right \rangle=0$ ， $\left \langle \psi_i \psi_j \right \rangle=\delta_{ij}(i,j=1,2)$ ， $\Delta t$ 是时间步长；函数 $H_i(i=1,2,3,4)$ 的表达式为：
$H_1=-\frac{1}{\tau}[\eta(t)+\sqrt{\frac{D\Delta t}{\tau^2}}(a_1\psi_1+b_1\psi_2)]$ ;
$H_2=-\frac{1}{\tau}[\eta(t)+\frac{\Delta t}{2}H_1+\sqrt{\frac{D\Delta t}{\tau^2}}(a_2\psi_1+b_2\psi_2)]$ ;
$H_3=-\frac{1}{\tau}[\eta(t)+\frac{\Delta t}{2}H_2+\sqrt{\frac{D\Delta t}{\tau^2}}(a_3\psi_1+b_3\psi_2)]$ ;
$H_1=-\frac{1}{\tau}[\eta(t)+\Delta tH_3+\sqrt{\frac{D\Delta t}{\tau^2}}(a_4\psi_1+b_4\psi_2)]$ .
其中 $a_1=a_2=\frac{1}{4}+\frac{\sqrt{3}}{6}$ , $b_{1,2}=\frac{1}{4}-\frac{\sqrt{3}}{6}\pm\frac{\sqrt{6}}{12}$ , $a_3=\frac{1}{2}+\frac{\sqrt{3}}{6}$ , $b_3=\frac{1}{2}-\frac{\sqrt{3}}{6}$ , $a_4=\frac{5}{4}+\frac{\sqrt{3}}{6}$ , $b_{4}=\frac{5}{4}-\frac{\sqrt{3}}{6}+\frac{\sqrt{6}}{12}$ 。

6.二值和三值噪声

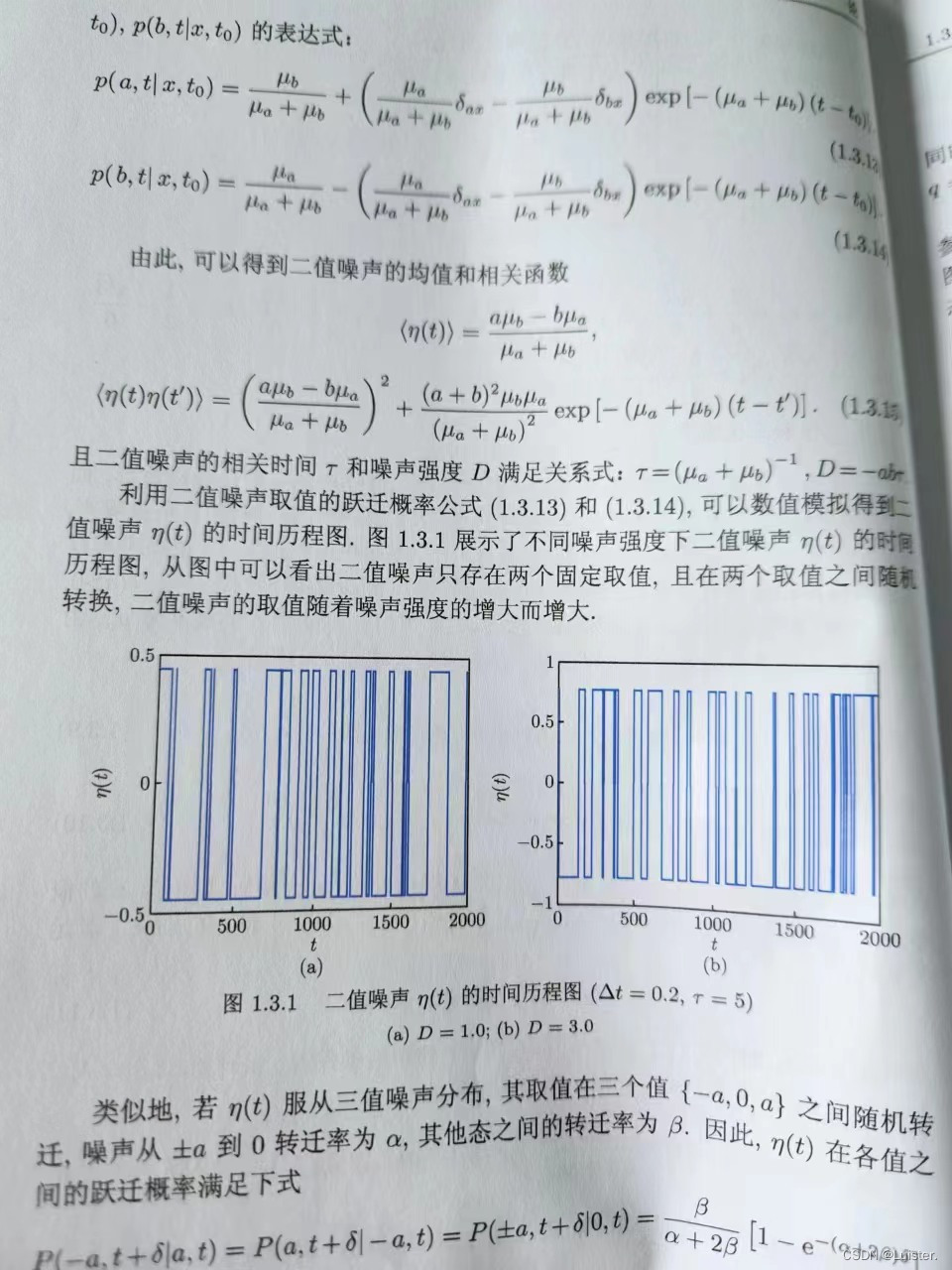
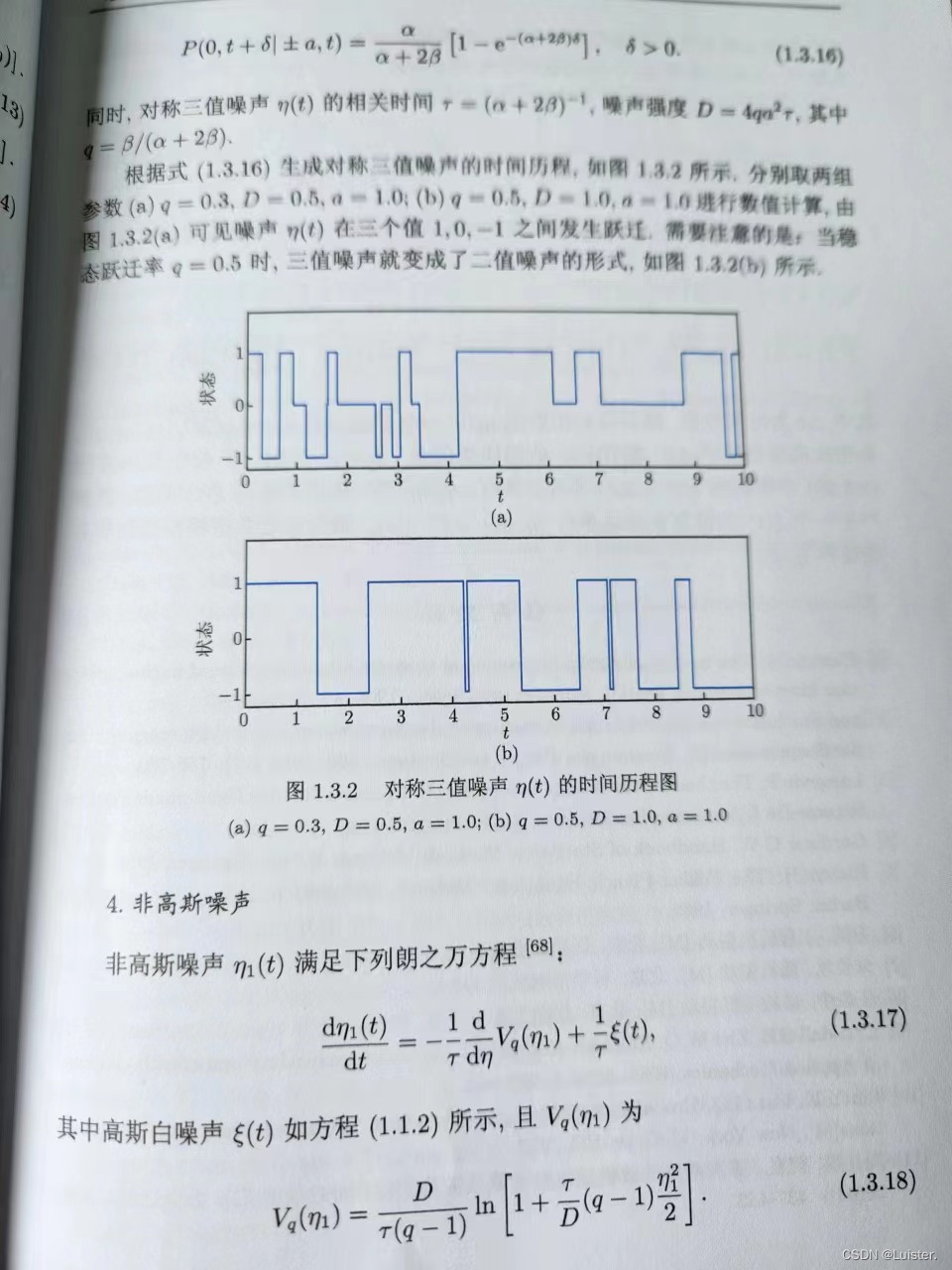
在这里插入图片描述

7.非高斯噪声

在这里插入图片描述

8.泊松过程、泊松噪声

%%
%泊松过程
% 定义参数lamba 
lamba = 1;

% 设置时间间隔dt和模拟时间T 
dt = 0.01;
T = 10;

% 计算生成事件的次数 
n = round(T/dt);

% 初始化时间和事件计数器 
t = zeros(n,1);
N = zeros(n,1);

% 使用泊松分布生成事件计数 
for i = 2:n
    N(i) = N(i-1) + poissrnd(lamba*dt);
    t(i) = t(i-1) + dt;
end

% 绘制泊松过程的图像 
stairs(t,N)%用于绘制阶梯状线条图
title('Poisson Process')
xlabel('Time')
ylabel('Number of events')

%%
%泊松噪声
%法1：
% 设置参数
lambda = 1; % 平均值
% 生成泊松噪声
t = 0:0.1:10; % 时间轴
y = poissrnd(lambda, size(t)); % 生成泊松噪声
plot(t,y); % 绘制泊松噪声
title('MATLAB自带函数生成的泊松噪声')
legend('\lambda=1');
%法2：
% 设置参数
lambda = 1; % 泊松分布的参数

% 生成噪声
n = 1000; % 生成1000个样本
poisson_noise = zeros(n, 1);
for i = 1:n
    r = rand; % 生成随机数
    k = 0;
    p = exp(-lambda); % 计算概率
    while(r > p)
        k = k + 1;
        p = p + exp(-lambda)*lambda^k/factorial(k); % 更新概率
    end
    poisson_noise(i) = k; % 记录样本
end

% 绘制噪声
figure(1)
plot(poisson_noise)
figure(2)
histogram(poisson_noise, 'Normalization', 'pdf') % 绘制直方图
xlabel('Poisson noise value')

![在这里插入图片描述](https://img-blog.csdnimg.cn/4f23368e4aab4b5fbd2ebb68ef7b403b.png

9.维纳过程

10.列维噪声（难）

11.Fortran实现噪声

program poisson_noise

    implicit none
    
    integer, parameter :: n = 100000 ! number of signals
    integer, parameter :: rate = 10 ! average rate of occurrence per interval
    real :: t0, t1, dt
    integer :: i, j
    integer :: count(n)
    
    call cpu_time(t0) ! Start timer
    
    do i = 1, n
        count(i) = 0
        do j = 1, 1000
            if (rand() < real(rate)/1000.0) then
                count(i) = count(i) + 1
            end if
        end do
    end do
    
    call cpu_time(t1) ! Stop timer
    dt = t1 - t0
    
    print *, "Average counts:", sum(count)/real(n)
    print *, "Time elapsed:", dt, "seconds"
    
end program