实例089 绘制蜗牛曲线（MFC单文档）

本文仅供学习交流，严禁用于商业用途，如本文涉及侵权请及时联系将于24小时内删除

目录

1.实验内容

2.实验原理

3.实验代码

4.示例拓展

1.实验内容

蜗牛线是一种常用的曲线，本实例演示的是如何在程序中绘制蜗牛曲线。

2.实验原理

蜗牛曲线（又称为等角螺线）是一种在极坐标系统中定义的曲线，其数学表达式可以表示为：

r=a+bθ

其中，r 是从原点到曲线上某点的距离，θ 是该点与正x轴之间的角度（通常以弧度为单位），a 和 b 是常数，分别控制曲线的起始半径和螺旋的紧密程度。通过改变 a 和 b 的值，蜗牛曲线可以表现出不同的形态。

如果 a 和 b 的符号相同（都是正数或都是负数），曲线会以原点为中心向外螺旋；如果 a 和 b 的符号相反，则曲线会在一定距离外开始螺旋，可能在中心附近形成一个环。

蜗牛曲线是一种常见的数学曲线，广泛应用于物理、工程和自然界中，例如在旋涡的形状描述、粒子在磁场中的运动轨迹等场合。

在笛卡尔坐标系下，蜗牛曲线的表达式通常不如在极坐标系下简洁。不过，对于特定类型的蜗牛曲线，比如说心脏线（cardioid）或其他形式的螺线，我们可以从极坐标系的表达式转换到笛卡尔坐标系。以心脏线为例，其在极坐标下的表达式是 r=a(1+cosθ)，其中 a 是常数。

将这种特定的蜗牛曲线表达式从极坐标转换为笛卡尔坐标系下，我们使用极坐标和笛卡尔坐标之间的转换公式：

x=rcosθ
y=rsinθ
代入 r=a(1+cosθ) 到上述转换公式中，我们得到：

x=a(1+cosθ)cosθ
y=a(1+cosθ)sinθ
这是心脏线的笛卡尔坐标表达式，它是一种特定的蜗牛曲线。

通过SetPixel函数来绘制曲线上的点来实现绘制蜗牛曲线。

SetPixel函数的语法如下：
COLORREF SetPixel( int x, int y, COLORREF crColor );
COLORREF SetPixel( POINT point, COLORREF crColor );
参数说明：
参数说明：
● x，y：指定点的横坐标和纵坐标。
● point：指定点的坐标。可以为该参数传递POINT结构或CPoint对象。
● crColor：绘制点的颜色。

3.实验代码

实现过程
（1）新建一个基于单文档的应用程序。
（2）主要程序代码如下：
void CMFC_实例宝典View::OnDraw(CDC* pDC)
{
	CMFC_实例宝典Doc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	
	/*if (!pDoc)
		return;*/
	double PI = 3.14;
	// TODO:  在此处为本机数据添加绘制代码

	pDC->SetWindowOrg(-200, -200);           //设置坐标原点
	//绘制蜗牛曲线
	for (double i = 0; i<40; i += PI / 600)
	{
		if (i == 0)
			pDC->SetPixel(0, 0, RGB(0, 128, 128));
		else
			pDC->SetPixel((20 * sin(i) / i*cos(i)) * 10, (20 * sin(i) / i*sin(i)) * 10, RGB(128, 128, 128));
	}

}

(3)实验结果

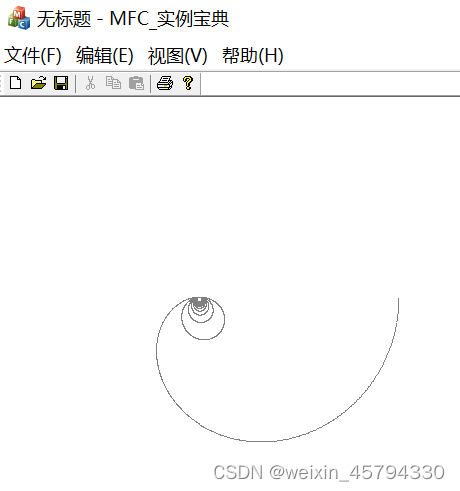
4.示例拓展

根据本实例，读者可以：设置点的颜色。