机器学习之正则化

正则化

如果我们有非常多的特征，我们通过学习得到的假设可能能够非常好地适应训练集（代价函数可能几乎为 0），但是可能会不能推广到新的数据。

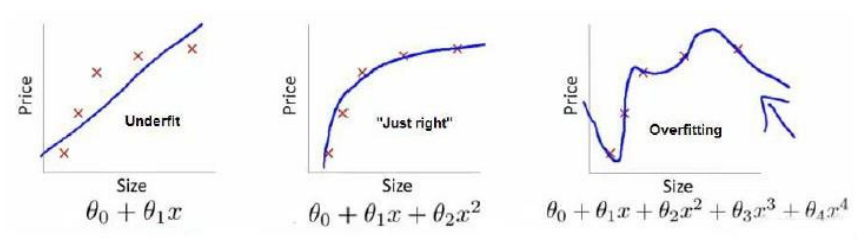
第一个模型是一个线性模型，欠拟合，不能很好地适应我们的训练集；第三个模型是一 个四次方的模型，过于强调拟合原始数据，而丢失了算法的本质：预测新数据。我们可以看出，若给出一个新的值使之预测，它将表现的很差，是过拟合，虽然能非常好地适应我们的 训练集但在新输入变量进行预测时可能会效果不好；而中间的模型似乎最合适。

分类问题中也存在这样的问题，就以多项式理解，𝑥 的次数越高，拟合的越好，但相应的预测的能力就可能变差。 问题是，如果我们发现了过拟合问题，应该如何处理？

• 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一 些模型选择的算法来帮忙（例如 PCA）
• 正则化。 保留所有的特征，但是减少参数的大小（magnitude）。

cost function

上面的回归问题中如果我们的模型是： ℎ𝜃 (𝑥) = 𝜃0 + 𝜃1𝑥1 + 𝜃2𝑥2 2 + 𝜃3𝑥3 3 + 𝜃4𝑥4

我们可以从之前的事例中看出，正是那些高次项导致了过拟合的产生，所以如果我们能 让这些高次项的系数接近于 0 的话，我们就能很好的拟合了。 所以我们要做的就是在一定程度上减小这些参数𝜃 的值，这就是正则化的基本方法。我 们决定要减少𝜃3和𝜃4的大小，我们要做的便是修改代价函数，在其中𝜃3和𝜃4 设置一点惩罚。 这样做的话，我们在尝试最小化代价时也需要将这个惩罚纳入考虑中，并最终导致选择较小 一些的𝜃3和𝜃4。

修改后的代价函数如下：

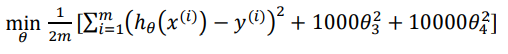
这样做的目的是弱化特征对拟合模型的影响，在不减少特征的情况下改变特征的权重。

然而我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚， 并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设：

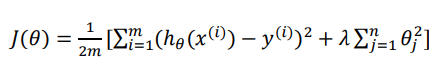
其中𝜆又称为正则化参数（Regularization Parameter）。 注：根据惯例，我们不对𝜃0 进 行惩罚。

如果选择的正则化参数 λ 过大，则会把所有的参数都最小化了，导致模型变成 ℎ𝜃 (𝑥) = 𝜃0，造成欠拟合。

那为什么增加的一项𝜆 = ∑ 𝜃𝑗 𝑛 2 𝑗=1 可以使𝜃的值减小呢？ 因为如果我们令 𝜆 的值很大的话，为了使 Cost Function 尽可能的小，所有的 𝜃 的值 （不包括𝜃0）都会在一定程度上减小。

但若 λ 的值太大了，那么𝜃（不包括𝜃0）都会趋近于 0，这样我们所得到的只能是一条 平行于𝑥轴的直线。 所以对于正则化，我们要取一个合理的 𝜆 的值，这样才能更好的应用正则化。

为什么 𝜆是一个标量而不是一个向量？

正则化参数理所应当可以是一个向量，目前不这么做的考虑主要是避免超参数过多，给模型调参带来过多的工作。最优的方案是算法自动为不同的参数选择不同的惩罚系数 𝜆。

详情论文可参考：

• https://dl.acm.org/doi/10.1145/2124295.2124313
• https://www.researchgate.net/publication/357366980_Theoretically_Accurate_Regularization_Technique_for_Ma-trix_Factorization_based_Recommender_Systems

Regularized Linear Regression

对于线性回归的求解，我们之前推导了两种学习算法：一种基于梯度下降，一种基于正规方程。

梯度下降

因为我们的cost function正则化不对𝜃0做处理，所以要分两种情况讨论。

在𝜃j的系数变为（1-a𝜆/m）,因为通常学习率a会较小，而m样本数量会较大，所以这个系数会很接近于1。可以看出正则化先行回个的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令𝜃减少一个额外的值（即每一次梯度下降都会对参数𝜃进行惩罚）。

正规方程

推导如下：

Regularized Logistic Regression

针对逻辑回归问题，我们已经学习过两种优化算法：我们首先学习了使用梯度下降法来优化代价函数𝐽(𝜃)，接下来学习了更高级的优化算法，这些高级优化算法需要你自己设计代价函数𝐽(𝜃)

自己计算导数同样对于逻辑回归，我们也给代价函数增加一个正则化的表达式，得到代 价函数：

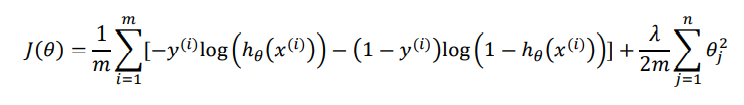
要最小化该代价函数，通过求导，得出梯度下降算法为：

看上去同线性回归一样，但是知道 ℎ𝜃 (𝑥) = 𝑔(𝜃 𝑇𝑋)，所以与线性回归不同。

小练习

假设你是工厂的产品经理，你对一些微芯片进行两种不同测试的结果。从这两个测试中，你想确定微芯片是合格还是

不合格。为了帮助您做出决定，您有一个测试结果的数据集（在过去的微芯片），你可以建立一个逻辑回归模型。

matlab

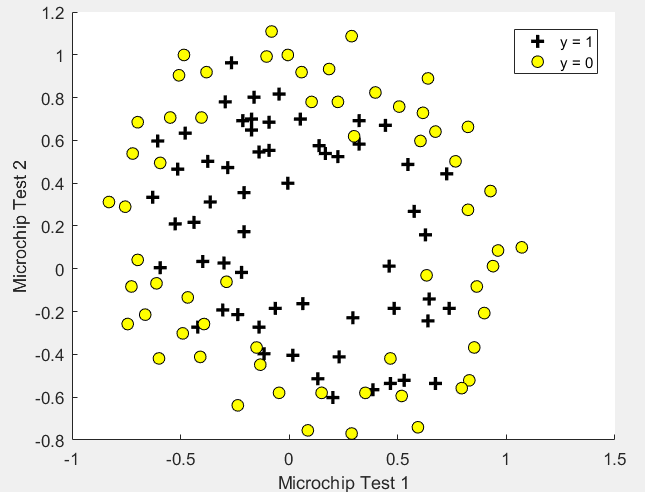
可视化初始数据

data = load('ex2data2.txt');
X = data(:, [1, 2]); y = data(:, 3);

pos = find(y==1); 
neg = find(y == 0);
plot(X(pos,1),X(pos,2),'k+','LineWidth',2,'MarkerSize',7);
plot(X(neg,1),X(neg,2),'ko','MarkerFaceColor','y','MarkerSize',7);

hold on;

xlabel('Microchip Test 1')
ylabel('Microchip Test 2')

legend('y = 1', 'y = 0')
hold off;

特征映射

X = mapFeature(X(:,1), X(:,2));

initial_theta = zeros(size(X, 2), 1);

lambda = 1;

mapFeature.m

function out = mapFeature(X1, X2)

degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end

end

得到X如下（28维）：

cost function

[cost, grad] = costFunctionReg(initial_theta, X, y, lambda);

costFunctionReg.m

function [J, grad] = costFunctionReg(theta, X, y, lambda)

m = length(y);
J = 0;
grad = zeros(size(theta));

[J, grad] = costFunction(theta, X, y);
 
J = J + lambda/(2*m)*(sum(theta.^2) - theta(1).^2); 
grad = grad + lambda/m*theta;
grad(1) = grad(1) - lambda/m*theta(1);

end

costFunction.m

function [J, grad] = costFunction(theta, X, y)

m = length(y); % number of training examples
J = 0;
grad = zeros(size(theta));

J = 1./m*(-y'*log(sigmoid(X*theta)) - (1-y)'*log(1-sigmoid(X*theta)));
grad = 1/m * X'*(sigmoid(X*theta) - y);

end

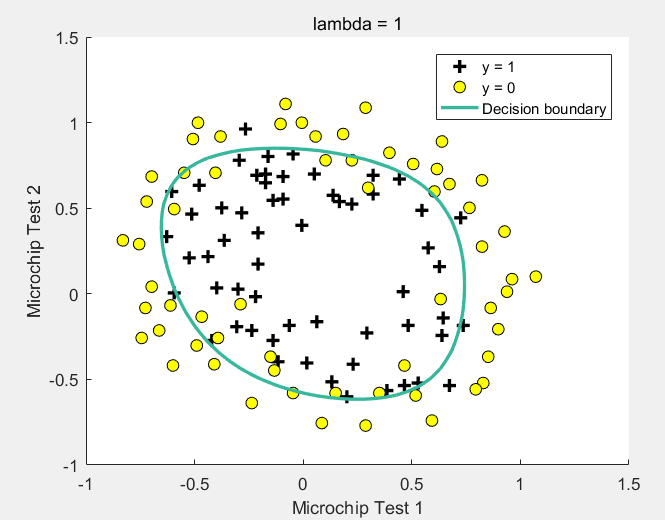
拟合参数边界可视化

initial_theta = zeros(size(X, 2), 1);
lambda = 1;
options = optimset('GradObj', 'on', 'MaxIter', 400);

[theta, J, exit_flag] = ...
	fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);

计算准确率

p = predict(theta, X);
fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100);
fprintf('Expected accuracy (with lambda = 1): 83.1 (approx)\n');

python

可视化初始数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path = 'ex2data2.txt'
df = pd.read_csv(path, header=None, names=['Test1', 'Test2', 'Accepted'])

positive = df[df['Accepted'].isin([1])]
negative = df[df['Accepted'].isin([0])]

fig, ax = plt.subplots(figsize=(12, 8))
ax.scatter(positive['Test1'], positive['Test2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative['Test1'], negative['Test2'], s=50, c='r', marker='x', label='Rejected')
ax.legend()
ax.set_xlabel('Test1 Score')
ax.set_ylabel('Test2 Score')
plt.show()

特征映射

def feature_mapping(x, y, power, as_ndarray=False):
    data = {'f{0}{1}'.format(i-p, p): np.power(x, i-p) * np.power(y, p)
                for i in range(0, power+1)
                for p in range(0, i+1)
           }
    if as_ndarray:
        return pd.DataFrame(data).values
    else:
        return pd.DataFrame(data)
        
x1 = df.Test1.values
x2 = df.Test2.values
Y = df.Accepted

data = feature_mapping(x1, x2, power=6)
data.head()

正则化代价函数

theta = np.zeros(data.shape[1])
X = feature_mapping(x1, x2, power=6, as_ndarray=True)
X.shape, Y.shape, theta.shape

def sigmoid(z):
    return 1 / (1 + np.exp(-z))
    
def cost(theta, X, Y):
    first = Y * np.log(sigmoid(X@theta.T))
    second = (1 - Y) * np.log(1 - sigmoid(X@theta.T))
    return -1 * np.mean(first + second)
    
    
def regularized_cost(theta, X, Y, l=1):
    theta_1n = theta[1:]
    regularized_term = l / (2 * len(X)) * np.power(theta_1n, 2).sum()
    return cost(theta, X, Y) + regularized_term

正则化梯度下降

def gradient(theta, X, Y):
    return (1/len(X) * X.T @ (sigmoid(X @ theta.T) - Y))
    
def regularized_gradient(theta, X, Y, l=1):
    theta_1n = theta[1:]
    regularized_theta = l / len(X) * theta_1n
#     regularized_theta[0] = 0
    regularized_term = np.concatenate([np.array([0]), regularized_theta])
    
    return  gradient(theta, X, Y) + regularized_term
#     return  gradient(theta, X, Y) + regularized_theta

拟合参数边界可视化

import scipy.optimize as opt
res = opt.minimize(fun=regularized_cost, x0=theta, args=(X, Y), method='Newton-CG', jac=regularized_gradient)
res

# 得到theta
def find_theta(power, l):
    path = 'ex2data2.txt'
    df = pd.read_csv(path, header=None, names=['Test1', 'Test2', 'Accepted'])
    df.head()

    Y = df.Accepted
    x1 = df.Test1.values
    x2 = df.Test2.values
    X = feature_mapping(x1, x2, power, as_ndarray=True)
    theta = np.zeros(X.shape[1])

#     res = opt.minimize(fun=regularized_cost, x0=theta, args=(X, Y, l), method='Newton-CG', jac=regularized_gradient)
    res = opt.minimize(fun=regularized_cost, x0=theta, args=(X, Y, l), method='TNC', jac=regularized_gradient)
    return res.x
    
    
# 决策边界，thetaX = 0, thetaX <= threshhold
def find_decision_boundary(density, power, theta, threshhold):
    t1 = np.linspace(-1, 1.2, density)
    t2 = np.linspace(-1, 1.2, density)
    cordinates = [(x, y) for x in t1 for y in t2]
    x_cord, y_cord = zip(*cordinates)
    mapped_cord = feature_mapping(x_cord, y_cord, power)
    
    pred = mapped_cord.values @ theta.T
    decision = mapped_cord[np.abs(pred) <= threshhold]
    
    return decision.f10, decision.f01
    
# 画决策边界
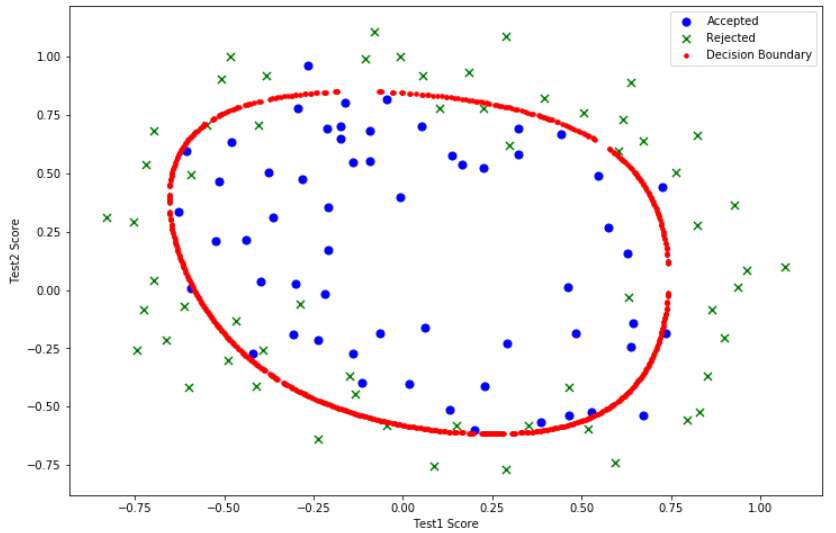
def draw_boundary(power, l):
    density = 1000
    threshhold = 2 * 10**-3
    
    theta = find_theta(power, l)
    x, y = find_decision_boundary(density, power, theta, threshhold)
    positive = df[df['Accepted'].isin([1])]
    negative = df[df['Accepted'].isin([0])]

    fig, ax = plt.subplots(figsize=(12, 8))
    ax.scatter(positive['Test1'], positive['Test2'], s=50, c='b', marker='o', label='Accepted')
    ax.scatter(negative['Test1'], negative['Test2'], s=50, c='g', marker='x', label='Rejected')
    ax.scatter(x, y, s=50, c='r', marker='.', label='Decision Boundary')
    ax.legend()
    ax.set_xlabel('Test1 Score')
    ax.set_ylabel('Test2 Score')

    plt.show()
    
    
draw_boundary(6, l=1)
draw_boundary(6, l=0)#过拟合
draw_boundary(6, l=100)#欠拟合

计算准确率

def predict(theta, X):
    probability = sigmoid(X @ theta.T)
    return probability >= 0.5
    return [1 if x>=0.5 else 0 for x in probability]
    
from sklearn.metrics import classification_report
Y_pred = predict(res.x, X)
print(classification_report(Y, Y_pred))