数学建模之拟合与插值

• 拟合算法

• 曲线拟合的最小二乘法

求一条曲线，使样本点均在此曲线的上下的不远处，所求的曲线叫为拟合曲线，它可以反映样本的总体分布，不至于出现局部较大的波动（龙格现象），能更好地反映出逼近函数的特性，在对给出的实验数据作曲线拟合时，使求得的逼近函数和已知函数之间的偏差的平方和达到最小，这就是最小二乘法的原理

1. 直线拟合

   1. 设样本点 (xi,yi)i=1,2,...,m分布为一条拟合曲线。

      表达式：y(x)=a0+a1x 其中，a0和a1为系数，表示截距和斜率。

      偏差平方和：，(a0,a1)=i=1nyi-a0-a1xi2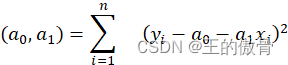最小。

2、多项式拟合

所给样本点的分布不能近似地呈一条直线，可用多项式拟合求寻求次数不多于m的表达式：y=a0+a1x+a2x2+...+anxm

偏差平方和：F(a0,a1)=i=1nyi-a0-a1xi-a2x22 最小。

例1：（预测人口）

x	2013	2014	2015	2016	2017	2018	2019	2020
y	9.6	12.9	17.1	23.2	31.4	38.6	50.2	63.0

Matlab代码：

x=2013:1:2020;
y=[9.6,12.9,17.1,23.2,31.4,38.6, 50.2,63.0];
subplot(1,2,1);
plot(x,y,'*');
title('人口散点图');
xlabel('年份');ylabel('人口');
p = polyfit(x,y,4);
yc=polyval(p,2021)
subplot(1,2,2);
plot(x,y,'*',x,polyval(p,x));
title('人口预测拟合模型图');
xlabel('年份');ylabel('人口');
legend('散点线','拟合曲线');

由计算可知预测2021年人口的人数为：79.8606（人）。

 注释：

[P,E]=polyfit（x,y,n）；返回同上的多项式P和误差值E。多项式系数在向量P中，E用在polyval函数中来计算误差（可省略）。x，y为对应的自变量，m为需要拟合的最高次幂。

yc=polyval(p,x)

其中p为多项式的系数，x为自变量，此函数的意义是计算以p为系数的多项式在各个自变量处的值，yc返回的就是计算出的值。

下面是运用 cftool运行的结果为：

 在cftool工具箱多次修改参数值与函数类型，结果如下图所示：

函数类型	Degree	SSE	R-square
Polynomial	1	104.6	0.9580
Polynomial	2	2.165	0.9991
Polynomial	3	1.602	0.9994
Polynomial	4	1.36	0.9995
Exponential		6.826	0.9973
Fourier		2.165	0.9991
Gaussian		1.629	0.9993
Interpolant		0	1

SSE是误差平方和。SSE越小，拟合的程度越好。

R—squre是拟合优度。这个参数越接近1，说明误差平方和越接近0，拟合程度越好。

故多项式中Degree为4的拟合效果最佳。

注意：两个参数都能评判拟合程度的好坏。

R—squre只能用于拟合函数是线性函数（相对于参数而言而不是变量）时，而SSE适用于所有情形。

当拟合函数不是线性函数时，用SSE评价就好了。

具体步骤：

1.在界面左侧这里输入x和y。

2.如果要设置其他拟合方式可以在界面右侧的这里进行选择。

3.在界面右侧会生成这样一个图像。

4.然后所求的结果这里就可以直接算出来。

曲线拟合的三种功能：

1.估算数据

2.预测趋势

3.总结规律

• 插值算法

1. 基础概念

已知样本点在区间（域）内若干点处的值，求样本点在该区间（域）内其他点处的值。

高次插值的Runge现象。

插值多项式的次数超过7次时，多项式会出现严重的外沿振荡现象。

例2：一天中24小时温度的变化

x	0	2	4	6	8	10	12	14	16	18	20	22	24
y	12	9	9	10	18	24	28	27	25	20	18	15	13

Matlab代码：

x=[0 2 4 6 8 10 12 14 16 18 20 22 24];		
y=[12 9 9 10 18 24 28 27 25 20 18 15 13];
x_1=13;
y_1=interp1(x,y,x_1,'spline') % y_1 = 27.8725
x_f=0:0.1:24;
y_f=interp1(x,y,x_f,'spline');
plot(x,y,'*',x_f,y_f,'r-');

 例3：Plane下轮廓线数据

x	0	3	5	7	9	11	12	13	14	15
y	0	1.2	1.7	2.0	2.1	2.0	1.8	1.2	1.0	1.6

Matlab代码：

x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x_2=0:0.1:15;
y_f1=Lagrange(x0,y0,x_2);
y_f2=interp1(x0,y0,x_2);
y_f3=interp1(x0,y0,x_2,'spline');
subplot(3,1,1);
plot(x0,y0,'*',x_2,y_f1,'-');
grid;
title('拉格朗日插值');
subplot(3,1,2);
plot(x0,y0,'*',x_2,y_f2,'-');
grid; 
title('线性插值');
subplot(3,1,3);
plot(x0,y0,'*',x_2,y_f3,'-');
title('三次样条插值');

1. 1. 小结：

.程序采用了Lagrange、分段线性和三次样条插值方法进行了计算，其中，Lagrange高次插值明显出现了Runge现象；因为Matlab没有Lagrange函数，所以程序写了高次插值函数Lageance，然后调用。

2.由图可知，三次样条插值曲线更光滑，效果最好。

例4：二维插值实例

测得平板表面3*5网格点处的温度分别为：82 81 80 82 84 79 63 61 65 81 84 84 82 85 86

试作出平板表面的温度分布曲面z=f(x,y)的图形。

Matlab代码：

x=1:5;
y=1:3;
z=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
figure(1);
mesh(x,y,z);
title('二维图');
x_1=1:0.1:5;
y_1=1:0.1:3;
z_1=interp2(x,y,z,x_1,y_1','cubic');% 注意y_1'是转置(列向量)
figure(2);
mesh(x_1,y_1,z_1);
title('插值后的二维图');
figure(3);
contour(x_1,y_1,z_1,10,'p');
title('插值后的等高线图');

• 拟合和插值的区别与联系

1.对给定任意样本点，刻画样本点反映的一般规律(给出曲线或者曲面函数)。

2.若要求所求曲线(面)通过所给所有样本点，就是插值问题。

3.若不要求曲线(面)通过所有样本点，而是要求它反映对象整体的变化趋势，这就是数据拟合，又称曲线拟合或曲面拟合。

4.求解问题具有确定的规律时(精确经过每个已知数据点)，采用插值方法。

5.求解问题具有随机性、不确定性的特点时，采用拟合方法。

备注：

1.一维函数使用样条插值，二维优先使用立方插值。

2.非线性拟合参数的计算则要应用高斯—牛顿迭代法。

3.当实验数据精度较高且数量较少是可以优先考虑插值，而实验数据精度较低且数目较多，而数据整体上呈现一定的趋势时可以考虑拟合。

4.离散数据求近似函数关系的问题为曲线拟合 。