一、描述机械臂(DH参数)
DH参数存在三种不同的描述。笔者在这个方面犯了一些错,所以特此记录一下。我采用的标准DH参数,不同类型的DH参数,建立的坐标系就不一样,所以需要注意一下。
标准DH参数建模的连杆坐标系是在连杆的传动轴,即连杆i的关节i+1上。由上右图可知,连杆1的驱动关节是Joint1,传动关节是Joint2,所以其坐标系要建立在Joint2上;同理Link2的连杆坐标系要建立在Jonit3上,以此类推,其他连杆的坐标系,如图所示。

如果需要得到DH参数,我们需要对自己的机械臂图进行测量。首先就是建立坐标系,六个轴要建立七个坐标系,因为底座也需要坐标系。总共就是link0到link6。这一步很重要,坐标轴的方向得按照运动的结构来确定,我的机械臂如图所示,所以建立坐标系如图所示。
接下来来最主要是理解杆长a,关节距离d。搞定这两个,其他的就是看图自行调整。其中要注意这里的单位是mm.我们之后matlab中输入的是m.


%机械臂为六自由度机械臂
%DH参数
% theta d a alpha
L(1)=Link([0 0.193 0 pi/2 ],'standard');
L(2)=Link([0 0 0.615 0 ],'standard');L(2).offset=pi/2;
L(3)=Link([0 0 0.571 0 ],'standard');
L(4)=Link([0 0.1775 0 -pi/2 ],'standard');L(4).offset=-pi/2;
L(5)=Link([0 0.118 0 pi/2 ],'standard');
L(6)=Link([0 0.1103 0 0 ],'standard');
angle=2*pi/180; %度
Robot=SerialLink(L,'name','UR10');二、solidworks机械结构的导入
我们上一节得到了机械臂的DH参数,然后进行了建模。我们用到了机器人工具箱,其中的知识希望读者自行搜索一下。接下来我们就要进行solidworks图的导入,最重要的是坐标系建立准确。建立准确后,会得到很好看的图片。如图所示。

%% 3D显示参数设置
q0 = [0 0 0 0 0 0];
v = [35 20];
w = [-2 2 -2 2 -1 2];
d = 'D:\matlab_code\matlab_arm_link\stl1\stl_5';
% Robot.plot3d(q0,'tilesize',1,'workspace',w,'path',d,'nowrist','view',v);
M = 'first.mp4';
Robot.plot3d(Qtraj,'tilesize',1,'workspace',w,'trail',{'r', 'LineWidth', 2},...
'path',d,'nowrist','view',v,'movie',M);
light('Position',[1 1 1],'color','w');其中的stl文件需要自己进行导入。

三、力矩仿真
力矩仿真需要查看机器人动力学参数,其动力学参数包括(m(关节质量),r(31的关节齿轮向量), I(3*3对称惯性矩阵), J(电机惯性Bm(粘性摩擦),Tc(库摩擦), G(齿轮传动比), qlim(关节变量上下限)
solidworks中,点击工具,其中的评估,选择质量属性。就能得到以下参数。

接下来需要从solidworks中得到关节质量和对称惯性矩阵。其余的参数需要根据不同的电机来得到。需要查看电机手册。
%% 物理参数
data=[
% Ixx, Iyy, Izz, Ixy, Iyz, Ixz, xc, yc, zc, m
0.088, 0.088, 0.039, 0, 0, 0, 0, 0, 0.65, 10.6;
0.224, 0.064, 0.172, 0, -0.90, 0, 0, -0.167, 0.096, 5.6;
2.369, 2.21, 0.172, 0, -0.585, 0, 0, -0.167, 0.627, 5.6;
1.225, 2.055, 0.860, 0.095, -0.113, -1.00, -0.525, -0.059, 0.629, 2.5;
1.359, 2.144, 1.016, 0.334, -0.394, -1.04, -0.538, -0.203, 0.633, 2.5;
1.633, 2.284, 0.861, 0.276, -0.394, -1.07, -0.538, -0.197, 0.765, 2.6
];使用机械臂工具箱中的力矩函数,.rne函数来得到力矩。他的函数输入是机械臂的角度,角速度,角加速度得到机械臂力矩。

接下来可以得到他的静力矩。
%% 静止力矩的计算
qd =zeros(num,6);
qdd =zeros(num,6);
qd_jing =zeros(1,6);
qdd_jing =zeros(1,6);
q_jing = [0 90 -90 90 0 0]*pi/180;
W = [0 0 5.56*9.8 0 0 0];
W1 = [0 0 0 0 0 0];
Q_jing = Robot.rne(q_jing,qd_jing,qdd_jing,'fext',W1 );
Robot.plot3d(q_jing,'tilesize',1,'workspace',w,'path',d,'nowrist','view',v);
之后可以通过蒙特卡洛算法来得到机械臂力矩的限制范围
%% 工作空间
% 参数
%关节角限位
q1_s=-160; q1_end=160;
q2_s=-225; q2_end=45;
q3_s=-45; q3_end=225;
q4_s=-110; q4_end=170;
q5_s=-100; q5_end=100;
q6_s=-266; q6_end=266;
%计算点数
num=50000;
% 求取工作空间
%设置轴关节随机分布,轴6不对工作范围产生影响,设置为0
q1_rand = q1_s + rand(num,1)*(q1_end - q1_s);
q2_rand = q2_s + rand(num,1)*(q2_end - q2_s);
q3_rand = q3_s + rand(num,1)*(q3_end - q3_s);
q4_rand = q4_s + rand(num,1)*(q4_end - q4_s);
q5_rand = q5_s + rand(num,1)*(q5_end - q5_s);
q6_rand = q6_s + rand(num,1)*(q6_end - q6_s);
q = [q1_rand q2_rand q3_rand q4_rand q5_rand q6_rand];
%正运动学计算工作空间
tic;
T_cell = cell(num,1);
[T_cell{:,1}]=Robot.fkine(q).t;%正向运动学仿真函数
disp(['运行时间:',num2str(toc)]);
% 分析结果
%绘制工作空间
t1=clock;
figure('name','机械臂工作空间')
hold on
plotopt = {'noraise', 'nowrist', 'nojaxes', 'delay',0};
Robot.plot([0 0 0 0 0 0], plotopt{:});
figure_x=zeros(num,1);
figure_y=zeros(num,1);
figure_z=zeros(num,1);
for cout=1:1:num
figure_x(cout,1)=T_cell{cout}(1);
figure_y(cout,1)=T_cell{cout}(2);
figure_z(cout,1)=T_cell{cout}(3);
end
plot3(figure_x,figure_y,figure_z,'r.','MarkerSize',3);
hold off
disp(['绘制工作空间运行时间:',num2str(etime(clock,t1))]);
%获取X,Y,Z空间坐标范围
Point_range=[min(figure_x) max(figure_x) min(figure_y) max(figure_y) min(figure_z) max(figure_z)];
disp(['X在空间坐标范围:',num2str(Point_range(1:2))]);
disp(['Y在空间坐标范围:',num2str(Point_range(3:4))]);
disp(['Z在空间坐标范围:',num2str(Point_range(5:6))]);通过蒙特卡罗随机给角度,角速度,角加速。
(1)角度范围 : -3.14 +3.14 rad;
(2)角速度范围 -3.14 +3.14 rad/s;
(3)角加速度范围 -3.14 +3.14 rad/s^2;
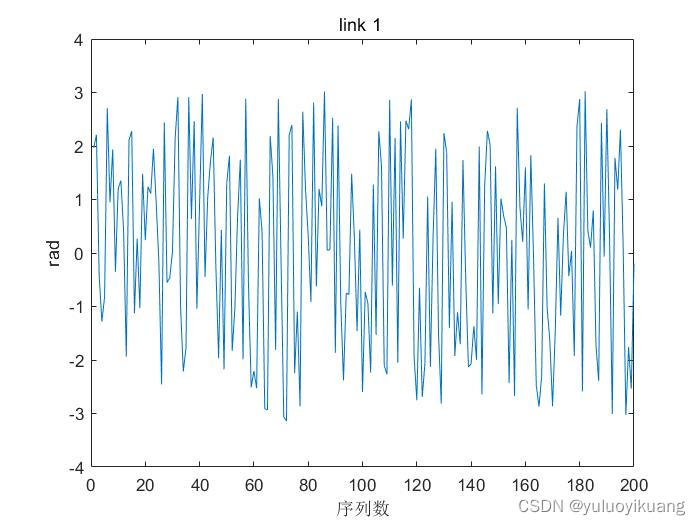
图1 link1的角度随机生成值的前两百个
随机50000组数据,随机组合。通过角度,角速度,角加速度得到力矩大小。其余图片不全部展示。
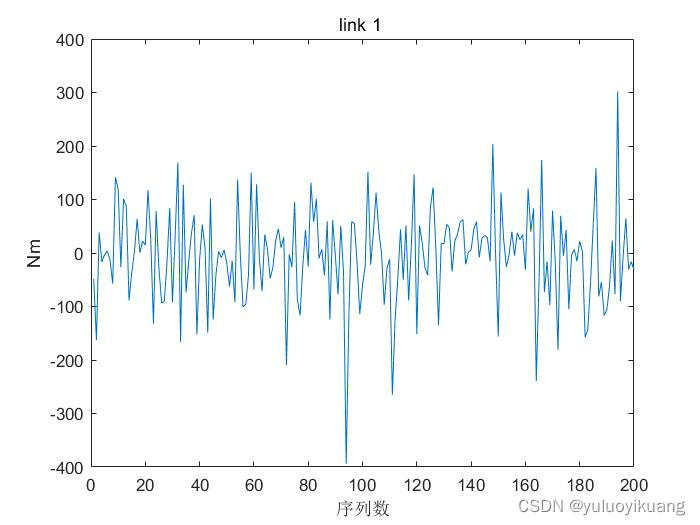
图2 link1的力矩值的前两百个
给定力矩限制,将超出力矩范围的角度,角速度,角加速度组合进行剔除。余下的角度,角速度,角加速度的组合留下。
给定力矩限制如下表所示.
表1 电机额定力矩经减速机后力矩输出表
| 电机型号 | 电压 | 最大持续电流 | 最大持续转矩 | 峰值转矩 | 减速比 | 经减速机后理论输出力矩 | 效率65% |
| voltage | Max Cont. Current | Max Cont. Torque | Peak Torque | drive ratio | Theoretical output torque | Actual output force Actual(Efficiency 65%) | |
| Motor model | VDC | A | Nm | Nm |
| Nm | Nm |
| TBM2G-05008A-ANNA-00 | 48 | 3.31 | 0.27 | 0.72 | 100 | 27 | 17.55 |
| TBM2G-06813C-ANNA-00 | 48 | 7.67 | 0.86 | 2.19 | 100 | 86 | 55.9 |
| TBM2G-06813C-ANNA-00 | 48 | 7.67 | 0.86 | 2.19 | 100 | 86 | 55.9 |
| TBM2G-08513D-ANNA-00 | 48 | 19.8 | 1.65 | 4.44 | 100 | 198 | 107.25 |
| TBM2G-08513D-ANNA-00 | 48 | 19.8 | 1.65 | 4.44 | 100 | 198 | 107.25 |
| TBM2G-11513C-ANNA-05 | 48 | 26.9 | 3.04 | 7.41 | 160 | 486.4 | 316.16 |
剔除超出力矩范围的组合之后得到力矩如下图所示
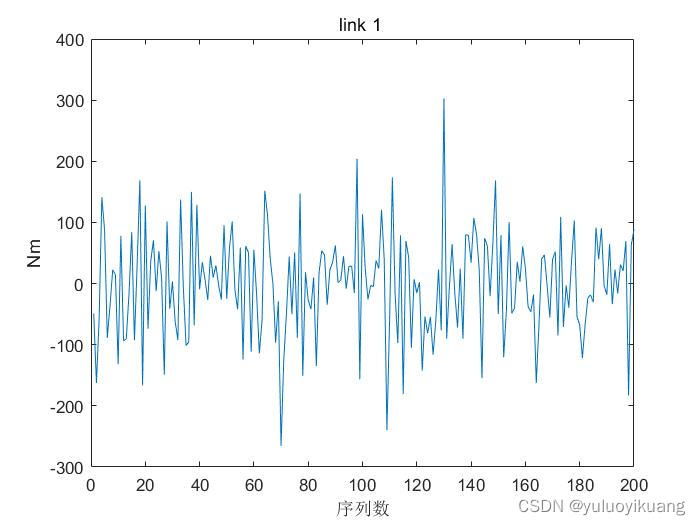
图3符合要求的力矩图
其力矩图所对应的角度图如下
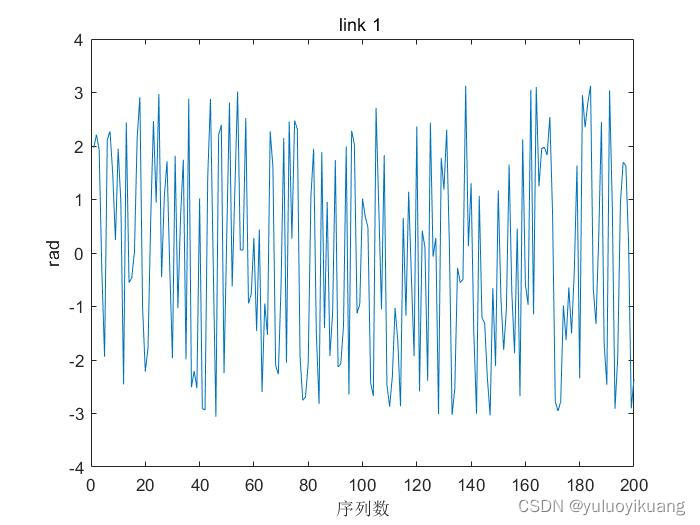
图4力矩对应的关节角度
通过其各个关节的角度可以反解出空间坐标
X在空间坐标范围:-1.1032 1.1008
Y在空间坐标范围:-1.079 1.1035
Z在空间坐标范围:-0.9541 1.2117

图5 运动空间图
极限加速度的求解
已知最大速度为3.14 rad/s ,最大力矩范围为
| jiont | Link1 | Link2 | Link3 | Link4 | Link5 | Link6 |
| Nm | 316.60 | 107.25 | 107.25 | 55.90 | 55.90 | 17.55 |
通过机械臂逆解得到,各个关节的角加速度最大值
| jiont | Link1 | Link2 | Link3 | Link4 | Link5 | Link6 |
| rad/s^2 | 12.08 | 10.26 | 7.51 | 5.49 | 34.51 | 5.99 |







 文章详细介绍了如何使用DH参数对六自由度机械臂进行建模,包括标准DH参数的坐标系建立、参数测量和Matlab中的编程实现。接着,讲述了如何将SolidWorks中的机械结构导入,并确保坐标系准确性。此外,还涉及了机械臂的力矩仿真,通过获取关节质量、惯性矩阵等动力学参数进行静态力矩计算,并利用蒙特卡洛方法确定工作空间和力矩限制。
文章详细介绍了如何使用DH参数对六自由度机械臂进行建模,包括标准DH参数的坐标系建立、参数测量和Matlab中的编程实现。接着,讲述了如何将SolidWorks中的机械结构导入,并确保坐标系准确性。此外,还涉及了机械臂的力矩仿真,通过获取关节质量、惯性矩阵等动力学参数进行静态力矩计算,并利用蒙特卡洛方法确定工作空间和力矩限制。
















 653
653

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








