三角波、正弦波和方波的频谱特点

最新推荐文章于 2025-05-14 00:04:57 发布

雪国流明

最新推荐文章于 2025-05-14 00:04:57 发布

阅读量7.5k

点赞数 7

分类专栏：信号处理文章标签：信号处理笔记

本文链接：https://blog.csdn.net/weixin_45915299/article/details/138470517

版权

信号处理专栏收录该内容

4 篇文章

订阅专栏

本文介绍了使用MATLAB实现对正弦波和三角波的频谱分析，展示了它们在频谱图上的特点，如正弦波的窄带宽和三角波的奇次谐波特性。同时，文中提到了如何通过FFT计算信号的频谱和给变量命名的学习要点。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

主要学习单/双边谱的特点，以及matlab实现方法

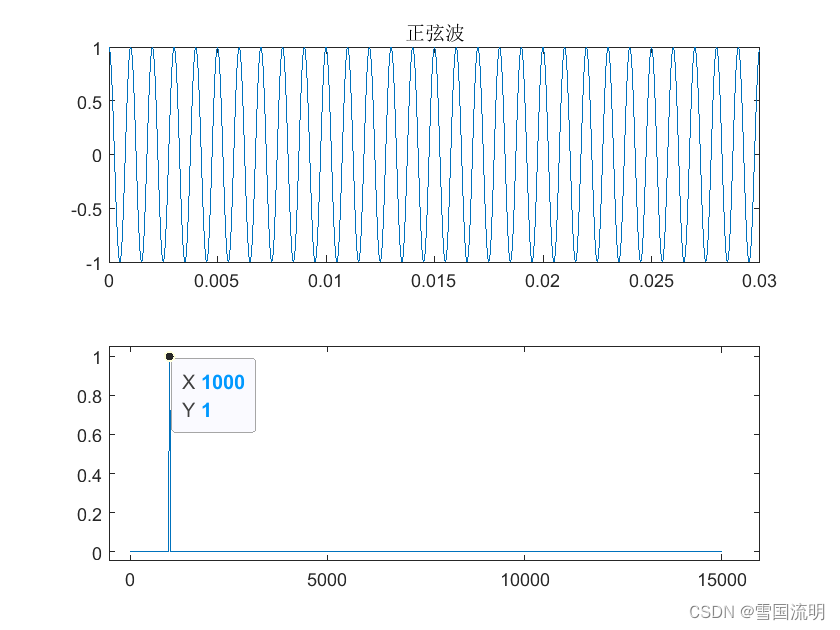
可以看到：正弦波的频谱图呈现出一个主要的频率峰值，而且频谱带宽很窄，主要集中在一个频率上。三角波频谱中包含了大量的奇次谐波，幅值随着频率的增加而逐渐衰减。正弦波的带宽相较三角波而言较小

PS：要狠狠学习一下写代码给变量取名字的方法

clc; clear; close all;
%% 定义三角波
T=0.03; %周期
fs=30000; t=0:1/fs:T-1/fs; %采样频率
f1=1000; %信号基频
x=sawtooth(2*pi*f1*t,0.5); %0.5指定标准三角波
subplot(211);plot(t,x); title('三角波');

%% 三角波fft计算频谱
N=length(x); %信号长度
Y=fft(x); 
P2=abs(Y/N); %双边频谱
P1=P2(1:N/2+1); %单边频谱
P1(2:end-1)=2*P1(2:end-1); %单边频谱翻倍
f=fs*(0:(N/2))/N;
subplot(212);plot(f,P1);

% f=linspace(0,fs,N);
% subplot(212);plot(f,abs(Y));

%% 定义正弦波
T1=0.03; %周期
fs1=30000; t1=0:1/fs1:T1-1/fs1; %采样频率
f2=1000; %信号基频
F_wave=cos(2*pi*f2*t1); %50是占空比
figure;
subplot(211);plot(t1,F_wave); title('正弦波');

%% 计算方波频谱
N1=length(F_wave);
Y1=fft(F_wave);
P4=abs(Y1/N1); %双边频谱
P3=P4(1:N1/2+1); %单边频谱
P3(2:end-1)=2*P3(2:end-1); %单边频谱翻倍
f_wave=fs1*(0:(N1/2))/N1;
subplot(212);plot(f_wave,P3);

% %% 定义方波
% T1=0.03; %周期
% fs1=30000; t1=0:1/fs1:T1-1/fs1; %采样频率
% f2=1000; %信号基频
% F_wave=square(2*pi*f2*t1,50); %50是占空比
% figure;
% subplot(211);plot(t1,F_wave); title('方波');
% 
% %% 计算方波频谱
% N1=length(F_wave);
% Y1=fft(F_wave);
% P4=abs(Y1/N1); %双边频谱
% P3=P4(1:N1/2+1); %单边频谱
% P3(2:end-1)=2*P3(2:end-1); %单边频谱翻倍
% f_wave=fs1*(0:(N1/2))/N1;
% subplot(212);plot(f_wave,P3);