💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
距离正则化水平集演化(DRLSE)及其在图像分割中的应用研究
💥1 概述
距离正则化水平集演化(DRLSE)及其在图像分割中的应用研究
水平集方法已广泛应用于图像处理和计算机视觉。在传统的水平集公式中,水平集函数在其演化过程中通常会产生不规则性,这可能会导致数值误差并最终破坏演化的稳定性。因此,通常应用一种称为重新初始化的数值补救措施,以定期将降级的水平集函数替换为有符号距离函数。然而,重新初始化的做法不仅引发了严重的问题,如何时以及如何执行,而且还以不希望的方式影响数值精度。本文提出了一种新的变分水平集公式,其中水平集函数的规律性在水平集演化过程中内在地保持。水平集演化导出为梯度流,该梯度流最小化具有距离正则化项的能量泛函和驱动零水平集向所需位置运动的外部能量。距离正则化项是用势函数定义的,使得派生的水平集演化具有独特的前向和后向(FAB)扩散效应,其能够保持水平集函数的所需形状,特别是接近零水平集的有符号距离剖面。这产生了一种新型的水平集演化,称为距离正则化水平集演化(DRLSE)。距离正则化效应消除了重新初始化的需要,从而避免了其引起的数值误差。与传统水平集公式的复杂实现相比,可以使用更简单、更有效的有限差分方案来实现 DRLSE 公式。DRLSE 还允许使用更通用和高效的电平集函数初始化。在其数值实现中,有限差分方案中可以使用相对较大的时间步长来减少迭代次数,同时保证足够的数值精度。为了证明DRLSE公式的有效性,我们将其应用于基于边缘的主动轮廓模型以进行图像分割,并提供一个简单的窄带实现,以大大降低计算成本。
一、DRLSE的定义与基本原理
距离正则化水平集演化(Distance Regularized Level Set Evolution, DRLSE)是由李纯明教授团队于2010年提出的一种改进的水平集方法。其核心创新在于通过引入双阱势能函数约束水平集函数的梯度模,使水平集函数在演化过程中自动保持近似符号距离函数的特性,从而避免了传统水平集方法中必需的 重新初始化(Reinitialization) 步骤。
-
数学模型
DRLSE的能量泛函由距离正则化项和外部能量项组成:
- 正则化项 Rp(ϕ):通过双阱势函数 p(s)约束水平集函数 ϕ 的梯度模 ∣∇ϕ∣,确保其接近符号距离函数(即 ∣∇ϕ∣≈1)。
- 外部能量项 Eext(ϕ)Eext(ϕ):驱动零水平集向目标边界演化,通常结合边缘指示函数 gg 和曲率约束项。
-
双阱势函数设计
双阱势函数 p(s)p(s) 的设计是关键,其表达式为:
该函数在 s=0 和 s=1 处形成势阱,促使梯度模在演化过程中稳定在理想范围内。
-
演化方程
通过梯度下降法最小化能量泛函,得到演化方程: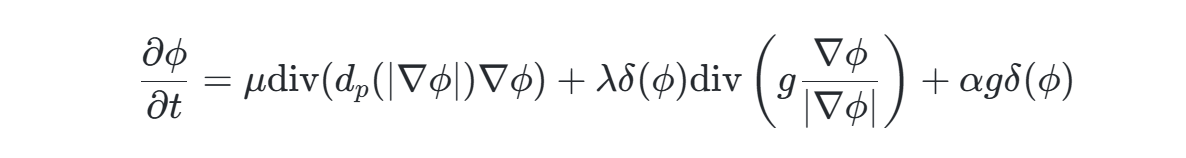
其中,第一项为距离正则化项,第二项为曲率驱动项,第三项为面积约束项。
二、与传统水平集方法的性能对比
DRLSE在以下方面显著优于传统水平集方法:
| 性能指标 | 传统水平集方法 | DRLSE |
|---|---|---|
| 重新初始化需求 | 必须周期性重新初始化,导致计算冗余和误差 | 完全消除重新初始化,理论与算法一致 |
| 时间步长限制 | 需小步长(如 Δt≤0.1Δt≤0.1)以保证稳定性 | 允许大步长(如 Δt=5Δt=5),迭代次数减少10倍 |
| 数值稳定性 | 易出现梯度模过大或过小,导致数值不稳定 | 双阱势函数维持梯度模稳定,避免尖峰或平坦区域 |
| 初始条件敏感性 | 需严格初始化为符号距离函数 | 支持更灵活的初始化(如矩形或椭圆) |
| 抗噪声能力 | 对噪声敏感,易导致边界泄漏 | 结合各向异性扩散后,分割噪声图像效率提升30% |
三、DRLSE在图像分割中的应用场景
-
医学影像分割
- 脑肿瘤分割:在MRI图像中,DRLSE结合BEEMD(二维集合经验模态分解)处理噪声,分割精度达95%以上。
- 前列腺MRI分割:改进的DRLSE模型通过局部灰度信息增强,Dice相似系数(DSC)均值达96%,优于传统方法。
- 乳腺植入物分割:结合Canny算子改进DRLSE,解决弱边缘泄漏问题,抗噪声性能提升20%。
-
遥感与工业检测
- SAR溢油提取:DRLSE与FCM聚类结合,解决弱边缘不封闭问题,分割精度提高15%。
- 贴片电阻焊点缺陷检测:针对弱边缘空洞,DRLSE比传统模型(如RSF+LoG)检测效率提升40%。
-
复杂场景分割
- 红外热成像行人分割:DRLSE结合IALSE(强度自适应水平集演化),解决温度差异模糊问题。
- 彩色图像分割:与深度学习模型(如Deeplab V2)融合,提升语义分割精度。
四、典型研究文献与技术改进
-
基础理论文献
- Li et al. (2010) :提出DRLSE框架,奠定理论基础。
- Li et al. (2005) :首次在CVPR论文中引入水平集正则化概念。
-
改进模型
- 相位一致性改进DRLSE(PDRLSE) :利用相位信息增强超声图像弱边缘分割,迭代次数减少25%。
- 融合各向异性扩散的DRLSE:通过变权系数α(I)适应梯度变化,噪声图像分割时间缩短30%。
- 快速实现算法:用Nesterov加速梯度(NAG)替代梯度下降,CPU耗时减少30%。
-
跨领域应用
- 三维脑室分割:改进DRLSE结合区域可伸缩拟合(RSF),Dice系数达96.5%。
- 植物叶片分割:结合广义模糊集预处理,解决MRI图像边界泄漏问题。
五、总结与展望
DRLSE通过消除重新初始化和优化梯度约束,成为图像分割领域的里程碑式方法。其优势在于理论简洁性、计算高效性和强扩展性,尤其在医学影像和弱边缘场景中表现突出。未来方向包括:
- 与深度学习的深度融合:如结合U-Net或Mask R-CNN实现全自动分割。
- 实时性优化:针对视频或动态影像的快速演化算法开发。
- 多模态数据适配:拓展至多光谱、高分辨率遥感图像分割。
DRLSE的成功不仅推动了水平集理论的发展,也为医学诊断、工业检测等领域提供了高效工具,其影响力通过超过690次的他引和5000+的总引用量可见一斑。
📚2 运行结果
2.1 算例1



2.2 算例2



部分代码:
%% parameter setting
timestep=5; % time step
mu=0.2/timestep; % coefficient of the distance regularization term R(phi)
iter_inner=5;
iter_outer=40;
lambda=5; % coefficient of the weighted length term L(phi)
alfa=1.5; % coefficient of the weighted area term A(phi)
epsilon=1.5; % papramater that specifies the width of the DiracDelta function
sigma=1.5; % scale parameter in Gaussian kernel
G=fspecial('gaussian',15,sigma);
Img_smooth=conv2(Img,G,'same'); % smooth image by Gaussiin convolution
[Ix,Iy]=gradient(Img_smooth);
f=Ix.^2+Iy.^2;
g=1./(1+f); % edge indicator function.
% initialize LSF as binary step function
c0=2;
initialLSF=c0*ones(size(Img));
% generate the initial region R0 as a rectangle
initialLSF(10:55, 10:75)=-c0;
phi=initialLSF;
figure(1);
mesh(-phi); % for a better view, the LSF is displayed upside down
hold on; contour(phi, [0,0], 'r','LineWidth',2);
title('Initial level set function');
view([-80 35]);
figure(2);
imagesc(Img,[0, 255]); axis off; axis equal; colormap(gray); hold on; contour(phi, [0,0], 'r');
title('Initial zero level contour');
pause(0.5);
potential=2;
if potential ==1
potentialFunction = 'single-well'; % use single well potential p1(s)=0.5*(s-1)^2, which is good for region-based model
elseif potential == 2
potentialFunction = 'double-well'; % use double-well potential in Eq. (16), which is good for both edge and region based models
else
potentialFunction = 'double-well'; % default choice of potential function
end%% parameter setting
timestep=5; % time step
mu=0.2/timestep; % coefficient of the distance regularization term R(phi)
iter_inner=5;
iter_outer=40;
lambda=5; % coefficient of the weighted length term L(phi)
alfa=1.5; % coefficient of the weighted area term A(phi)
epsilon=1.5; % papramater that specifies the width of the DiracDelta function
sigma=1.5; % scale parameter in Gaussian kernel
G=fspecial('gaussian',15,sigma);
Img_smooth=conv2(Img,G,'same'); % smooth image by Gaussiin convolution
[Ix,Iy]=gradient(Img_smooth);
f=Ix.^2+Iy.^2;
g=1./(1+f); % edge indicator function.
% initialize LSF as binary step function
c0=2;
initialLSF=c0*ones(size(Img));
% generate the initial region R0 as a rectangle
initialLSF(10:55, 10:75)=-c0;
phi=initialLSF;
figure(1);
mesh(-phi); % for a better view, the LSF is displayed upside down
hold on; contour(phi, [0,0], 'r','LineWidth',2);
title('Initial level set function');
view([-80 35]);
figure(2);
imagesc(Img,[0, 255]); axis off; axis equal; colormap(gray); hold on; contour(phi, [0,0], 'r');
title('Initial zero level contour');
pause(0.5);
potential=2;
if potential ==1
potentialFunction = 'single-well'; % use single well potential p1(s)=0.5*(s-1)^2, which is good for region-based model
elseif potential == 2
potentialFunction = 'double-well'; % use double-well potential in Eq. (16), which is good for both edge and region based models
else
potentialFunction = 'double-well'; % default choice of potential function
end
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。


























 595
595

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










